Kezdőlap


Feladat:	F.2173	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bacsi Zsuzsanna , Bakó I. , Barla F. , Beleznay F. , Benkő B. , Buczolich Z. , Csákány Anikó , Erdélyi T. , Gulácsi F. , Hajnal P. , Hochenburger R. , Horváth 169 T. , Kántor Zs. , Kelemen B. , Kiss A. , Korondi P. , Kőrösi G. , Kovács I. , Márkus L. , Sárkány Ágnes , Soós Marianna , Szegedy P. , Szodfridt G. , Tóth T. , Umann G. , Varga K. , Varga Lívia , Varga T. , Winkler R.
Füzet:	1979/március, 111 - 114. oldal		PDF \| MathML
Témakör(ök):	Eltolás, Sík parkettázás, Feladat
Hivatkozás(ok):	Feladatok: 1978/november: F.2173

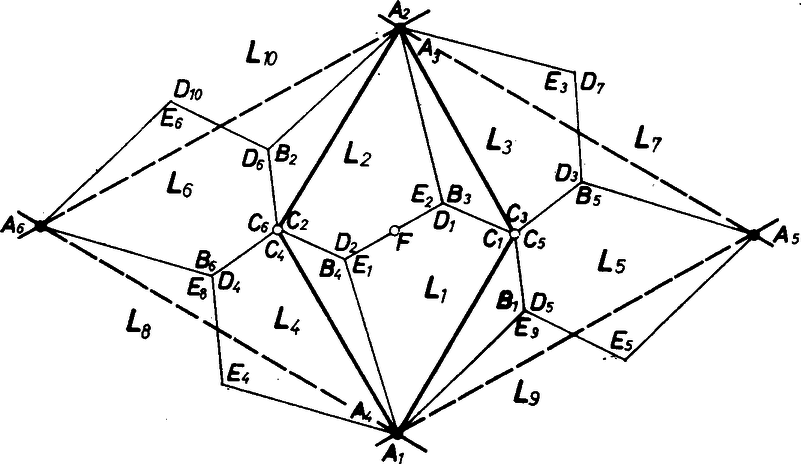
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ötszögek alábbi lerakásában minden ötszög $A B C D E$ betűzése pozitív körüljárású lesz, és ötszög csúcsa sehol sem esik egybe másik ötszög kerületének két csúcs közé eső pontjával. Így ‐ mivel az ötszögnek általában nincs $D E$ -vel egyenlő oldala ‐ egy $L_{1}$ ötszöglemez $D_{1}$ és $E_{1}$ csúcsával a $D_{1} E_{1}$ oldalon szomszédos $L_{2} (≅ L_{1})$ ötszöglemezből csak az $E_{2}$ , ill. $D_{2}$ csúcs eshet egybe. Eszerint $L_{2}$ az $L_{1}$ tükörképe lesz a $D_{1} E_{1}$ szakasz $F$ felezőpontjára.

Letéve ezeket, a

D_{1}

E_{1}

pontok környezetében marad lefedetlen szögtartomány, éspedig akkora, mint- az ötszög

B

-nél levő szöge, hiszen

\begin{matrix} A B C ∢ + C D E ∢ + D E A ∢ = 540^{\circ} - (60^{\circ} + 120^{\circ}) = 360^{\circ}, \\ 360^{\circ} - (C_{1} D_{1} E_{1} ∢ + D_{2} E_{2} A_{2} ∢) = A B C ∢ . \end{matrix}

Eszerint a

C_{1} D_{1} A_{2}

és

C_{2} E_{1} A_{1}

szögtartományok lefedhetők egy

L_{3}

és

L_{4}

ötszög

B

-nagyságú szögtartományával, méghozzá ezek

C

- és

A

-típusú csúcsai éppen a

C_{1}

A_{2}

pontpárba esnek, ill.

L_{4}

-éi a

C_{2}

A_{1}

párba, hiszen

A E = A B

és

C D = C B

alapján a

C_{1} D_{1} A_{2}

(más néven:

C_{1} E_{2} A_{2}

) és

C_{2} E_{1} A_{1}

(azaz

C_{2} D_{2} A_{1}

) háromszögek egyező körüljárásúan egybevágók ötszögeink

A B C

részháromszögével. Ennélfogva

A_{1} C_{2} = A_{1} C_{1}

, továbbá

\begin{matrix} C_{1} A_{1} C_{2} ∢ = C_{1} A_{1} E_{1} ∢ + D_{2} A_{1} C_{2} ∢ = B_{1} A_{1} C_{1} ∢ + C_{1} A_{1} E_{1} ∢ = B_{1} A_{1} E_{1} ∢ = 60^{\circ}, \end{matrix}

tehát a centrálszimmetrikus

A_{1} C_{1} A_{2} C_{2}

idom

60^{\circ}

-os szögű rombusz. Az

L_{3}

és

L_{4}

idomok is egymás képei az

F

centrumra. Azt találtuk, hogy ötszögünk 3 példánya úgy illeszthető egy pontba a

B

, az

E

, a

D

csúcsával (pozitív körüljárással), hogy hézagtalanul, átfedésmentesen lefedik a pont környezetét és az e pontból kiinduló, egymáshoz csatlakozó oldalszakaszok külső végpontjai is egybeesnek (rendre az

A

- és

A

-, majd

D

- és

E

-, végül a

C

- és

C

-típusú csúcsok).
Az eddig lefedett síkrész határán

C_{1}

-ben és

C_{2}

-ben

360^{\circ} - 2 \cdot 120^{\circ} = 120^{\circ}

a lefedetlen szögtartomány, ezt lefedjük, ha egy

L_{5}

idom

C_{5} D_{5}

oldalát

C_{1} B_{1}

-re tesszük, ill. egy

L_{6}

-ból a

C_{6} D_{6}

oldalt.

C_{2} B_{2}

-re. Más szóval:

L_{5}

L_{1}

-nek,

L_{6}

L_{2}

-nek elforgatottja

+ 120^{\circ}

-kal, eszerint az

A_{1} A_{5} A_{2} A_{6}

idom rombusz, az

A_{1} A_{2}

átló végpontjaiban

120^{\circ}

-os szögekkel.
Mivel

A_{4} E_{4}

(azaz

A_{1} E_{4}

) és

A_{3} E_{3}

(azaz

A_{2} E_{3}

) egymás képei

F

-re, másrészt

A_{6} B_{6}

képe az

A_{4} E_{4}

-nek, azért

A_{2} E_{3} = A_{3} E_{3}

-at eltolás viszi át

A_{6} B_{6}

-ba, vagyis

L_{3}

-at az

L_{4}

és

L_{6}

közé illeszthető

L_{8}

-ba (amit

E_{8}

-nál fogva illesztünk

D_{4}

-hez). Ugyanígy az

\vec{A_{6} A_{2}}

vektorú eltolás

L_{4}

-et ráviszi az

L_{3}

és

L_{5}

közé illesztett

L_{7}

-re, és hasonlóan

\pm \vec{A_{5} A_{2}}

vektorú eltolás

L_{5}

-öt

L_{2}

és

L_{6}

közé

L_{10}

-be,

L_{6}

-ot

L_{1}

és

L_{5}

közé

L_{9}

-be. Mondjuk ki ezeket így: az

A_{1} A_{5} A_{2} A_{6}

rombusz egyirányú

A_{1} A_{5}

és

A_{6} A_{2}

oldalai fölött keletkezett

A_{1} B_{1} E_{5} A_{5}

és

A_{6} E_{6} B_{2} A_{2}

"díszítmények'' egymásba tolhatók, és ugyanígy a másik oldalpár díszítményei is.
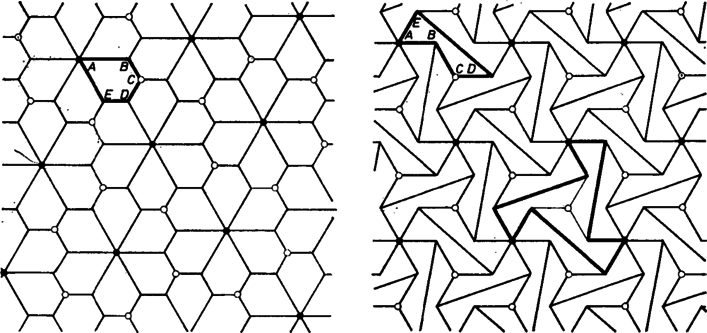
Ha tehát

60^{\circ}

-os szögű rombuszrácsot veszünk

A_{1} A_{2} = 2 \cdot A F

hosszúságú alapvektorokkal, és minden elemi cellájához hozzárendeljük az

L_{1} - L_{6}

ötszögegyüttes (= "molekula'') egy másolatát, ezzel hézagtalanul és egyrétűen lefedtük a síkot, minden egyes díszítmény mindegyik foga lefedi a szomszédos foghíjait, ill. foghíját befedi a szomszéd molekula foga.
Azt is látjuk, hogy így a rombuszrács minden egyes rácspontjában

2 + 1 + 2 + 1 = 6

db ötszög fut össze a

60^{\circ}

-os szögével, továbbá hogy a

C

pontok a rácsunkban található egységnyi oldalú szabályos háromszögek középpontjai.
Ábráink mutatják, hogy a

B

D

és

E

csúcsok mindegyikében lehet

180^{\circ}

-nál nagyobb szög. Egyikben

B ∢ = 240^{\circ}

-ot vettünk, és még az

A B = B C

speciális esetet. Két ilyen ötszög paralelogrammává egyesíthető, és így ‐ a fönti többlettulajdonságokat föladva ‐ végtelen sokféle lefedés készíthető belőle.

Megjegyzések. 1. Bizonyítható úgy is az állítás, hogy elindulásul ‐ mintegy ösztönösen ‐ 3 db ötszöglemez

120^{\circ}

-os szögét fogjuk össze, leírjuk az együttes határvonalát, szimmetriáját, és ezt a "molekulát'' illesztjük be egy olyan rács minden egyes csomópontjába, amilyet az egybevágó szabályos hatszögekből alakuló lefedés csomópontjai alkotnak. Vagy úgy, hogy tükrözzük ezt az együttest egyik

D E

-típusú oldalának felezőpontjára, és a kapott, 6 atomból épült molekulát építjük be

60^{\circ}

-os rombuszrácsba. ‐ Természetesen adódó molekula az

A

-típusú csúcsaiknál összefogott 6 db ötszög is.
2. Különösen tetszetős lefedést ad a tengelyszimmetrikusnak fölvett ötszög:

B ∢ = D ∢ = 120^{\circ}

és

D E = C D = A B / 2

. De hiába vannak tengelyes szimmetriái a rácsnak is, az eredő lefedésnek még sincsenek tengelyei, mert az

A

-csomók körüli 6-ágú és a

C

-csomók körüli 3-ágú csillagok tengelyei nem közösek.
Egészen más a "varázsa" a nem konvex alapötszögekből alakuló lefedéseknek, mélyebben egymásba fogazódásukkal. Ezek azonban már nem csak matematikai kérdések.

3. Lényeges tulajdonsága a leírt lefedésnek : bárhogyan kiválasztott két ötszögéhez van olyan transzformációja a síknak (eltolás vagy forgatás), amely az elsőt a másikba viszi és egyidejűen az egész lefedés bármelyik ötszögét egy másik (egész) ötszögébe, szóval az egész lefedést önmagába. Ismételjük kiindulásunkat is, bár kissé másképpen: lefedésünk csomópontjaiban nincs

180^{\circ}

-os "szög". Ezekkel az "erős" megkötésekkel vizsgálta a sík lefedését egybevágó ötszögekkel egy régebbi cikkünkben Bollobás Béla^{$^{*}$}. Feladatunkat ebből a tételéből vettük (hozzátéve a nem konvex esetek kérdését): megengedve a tengelyes tükrözést is,

4

olyan ötszögtípus ‐ és hozzájuk alkalmas lerakásmód ‐ van, amelyekkel a sík hézagtalanul, egyrétűen és az előbbi két megkötés mellett parkettázható.
Mihelyt engedünk valamit e követelményekből, mindjárt emelkedik az ötszögtípusok, lerakásmódok száma. Szép példákat láthatott erre az olvasó dr. Perjés Zoltánnak az Élet és Tudomány c. folyóirat 1978. évi 47. számában megjelent cikkében. (Érdekes véletlen volt a mondott cikk, másrészt ezen feladatunk majdnem "napra pontosan" egyidejű megjelenése.)
Borítólapunk hátoldalán más típusú lefedés látható egyenlő oldalú ötszögekből, szögeik rendre

60^{\circ}

160^{\circ}

80^{\circ}

100^{\circ}

140^{\circ}

. (Itt kicsinyítve látható.) (A New South Wales-i Parabola alapján, vö. F. 2191. is).

^{$^{*}$}A sík lefedése egybevágó konvex sokszögekkel. 2. közlemény: Az egyenletes ötszög‐parkettázások, K.M.L: 22 (1961) 193‐200. oldal