Kezdőlap


Feladat:	F.2172	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/március, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Oldalfelező merőleges, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1978/november: F.2172

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A szokás szerint megbetűzött $A B C$ háromszögben az $n_{a}$ szakasz a $B C = a$ oldal $A_{1}$ felezőpontjából indul, $A_{2}$ végpontja pedig az $A$ -ból $B$ -be vivő oldalon van, mert $c > b$ , azaz $A B > A C$ miatt $B$ van a felező merőlegesnek $A$ -val ellentétes oldalán. Hasonlóan $A B$ -n van $n_{b} = B_{1} B_{2}$ végpontja. Így $n_{a}$ is, $n_{b}$ is az $A_{1} B_{1}$ és $A B$ párhuzamos egyenesek egy-egy pontját köti össze. Az egyenespárral alkotott $β'$ , ill. $α'$ hajlásszögeikre (1. ábra)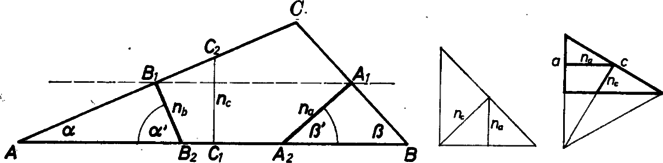

\begin{matrix} β' = 90^{\circ} - β < 90^{\circ} - α = α' \end{matrix}

‐ ugyanis az adott nagyságviszony alapján a

α < β < γ

, és így

β < 90^{\circ}

‐, ezért valóban a laposabban hajló

A_{1} A_{2}

nagyobb

B_{1} B_{2}

-nél.

A második állítás a

C_{1} C_{2} A

és

B_{1} B_{2} A

háromszögek hasonlóságából következik, ugyanis az előzőkhöz hasonló meggondolás szerint

C_{2}

A C

oldalon van;

A C_{1} = c / 2 > b / 2 = A B_{1}

miatt a megfelelő másik befogókra

C_{1} C_{2} > B_{1} B_{2}

2. Az

n_{a}

és

n_{c}

szakaszok nagyságviszonyáról csak azt mondhatjuk, hogy mindhárom lehetőség fennáll. Elég ennek igazolására számpéldákat (ill. példatípusokat) mutatnunk. Speciálisan derékszögű háromszögeket választunk, ezekben

c = 1

megválasztással

n_{c} = a / 2 b

és

n_{a} = b / 2

. Köztük egyenlőség áll, ha

b_{0}^{2} = a_{0}

, amikor a Pitagorasz-tétel alapján

a_{0}^{2} + a_{0} = 1

, ennek az egyenletnek a pozitív gyöke

\begin{matrix} sin α_{0} = a_{0} = \frac{\sqrt[]{5} - 1}{2} = 0, 618, \end{matrix}

és ekkor

α_{0} < 45^{\circ} < β_{0}

, mert mint könnyen megmutatható,

\begin{matrix} \frac{\sqrt[]{5} - 1}{2} < \frac{\sqrt[]{2}}{2} = sin 45^{\circ} . \end{matrix}

Ha most

α > α_{0}

, de még

α < 45^{\circ}

, akkor

\begin{matrix} \frac{1}{\sqrt[]{2}} > a > a_{0} és b_{0} = cos α_{0} > cos α = b > \frac{1}{\sqrt[]{2}}, \end{matrix}

ezért

\begin{matrix} b^{2} < b_{0}^{2} = a_{0} < a \end{matrix}

és

\begin{matrix} n_{c} = \frac{a}{2 b} > \frac{a_{0}}{2 b} > \frac{a_{0}}{2 b_{0}} = n_{c 0} = n_{a 0} = \frac{b_{0}}{2} > \frac{b}{2} = n_{a} . \end{matrix}

(A föltevésünk érvényességét határoló

a = b

esetben

n_{c} = \sqrt[]{2} n_{a}

.)
Ha viszont

α < α_{0}

, speciálisan

α = 30^{\circ}

mellett

n_{a}

fele akkora, mint az 1 oldalú szabályos háromszög magassága,

n_{c}

viszont harmada annak. Ekkor valóban

α < α_{0}

, mert

\frac{1}{2} < \frac{\sqrt[]{5} - 1}{2}

. ‐ Mindhárom nagyságviszony esetére példát adtunk, állításunkat igazoltuk.

II. megoldás. A háromszög bármelyik oldalát kiválasztva, annak oldalfelező merőlegese a másik két oldal közül mindig a hosszabbat metszi, mert a szemben fekvő csúcs azon a félsíkon van, amelyiken az oda vivő rövidebbik oldal. Így az

n_{a}

és

n_{b}

szakaszokat a

c

oldal, az

n_{c}

-t pedig a

b

oldal fogja határolni. Kifejezhetők tehát a szakaszok az oldalak és a szögek segítségével a következőképpen:

\begin{matrix} n_{a} = \frac{a tg β}{2}, n_{b} = \frac{b tg α}{2}, n_{c} = \frac{c tg α}{2} . \end{matrix}

Felhasználjuk még, hogy

a = 2 r sin α

b = 2 r sin β

c = 2 r sin γ

. Ezekkel a szakaszok páronkénti arányai

\begin{matrix} \frac{n_{a}}{n_{b}} = \frac{a tg β}{b tg α} = \frac{a \frac{sin β}{cos β}}{b \frac{sin α}{cos α}} = (\frac{a}{b} \cdot \frac{sin β}{sin α}) \cdot \frac{cos α}{cos β} = \frac{cos α}{cos β} > 1, \end{matrix}

mert a föltevés szerint

α < β (< γ)

mindkettő hegyesszög; másrészt

\begin{matrix} \frac{n_{c}}{n_{b}} = \frac{c tg α}{b tg α} = \frac{c}{b} > 1. \end{matrix}

Ezzel az állítás két egyenlőtlenségét beláttuk.
Végül a kérdéses nagyságviszony vizsgálata céljára a

2 sin x cos y = sin (x + y) + sin (x - y)

azonosság alapján így alakíthatjuk a két szakasz arányát:

\begin{matrix} \frac{n_{c}}{n_{a}} = \frac{sin γ tg α}{sin α tg β} = \frac{sin γ cos β}{cos α sin β} = \\ = \frac{sin (γ + β) + sin (γ - β)}{sin (β + α) + sin (β - α)} = \frac{sin α + sin (γ - β)}{sin (β - α) + sin γ} . \end{matrix}

A számláló és a nevező tagjai pozitívok. Elérhető, hogy ugyanaz a nagyságviszony álljon fönn elöl álló tagjaik közt, mint másodiknak írt tagjaik közt, és ekkor ugyanez teljesül

n_{c}

és

n_{a}

közt is. Mármost

\begin{matrix} sin (γ - β) > sin γ és sin α > sin (β - α) \end{matrix}

egyidejű teljesüléséhez elegendő, ha

γ > 135^{\circ}

és

α > β - α

, vagyis

2 α > β > α

, az ellentétes nagyságviszony pedig mindig beáll, ha

2 α < β < γ < 90^{\circ}

. Könnyen találhatók e feltételeknek eleget tevő

α

β

γ

értékhármasok.
Ezek után azt már fölösleges keresnünk, beállhat-e

n_{a} = n_{c}