Kezdőlap


Feladat:	F.2168	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Misota Gábor , Pintér Ferenc
Füzet:	1979/március, 104 - 106. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Terület, felszín, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1978/október: F.2168

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először olyan $P$ pontok esetére igazoljuk az állítást, amelyek az $A_{1} A_{2} A_{3}$ háromszög $F_{1} F_{2} F_{3}$ középháromszögének belsejében vannak ( $F_{1}$ felezi az $A_{2} A_{3}$ oldalt s í. t.). Ekkor $P$ rajta van mindegyik $B_{i} C_{i}$ szakaszon, és mint könnyen belátható, benne van mind a $C_{1} C_{2} C_{3}$ , mind a $D_{1} D_{2} D_{3}$ háromszögben, ezek területeit a $P C_{i}$ , $P D_{i}$ szakaszok úgy osztják részekre, hogy a 3-3 rész területének összege az illető háromszög $t_{C}$ , $t_{D}$ területét adja.

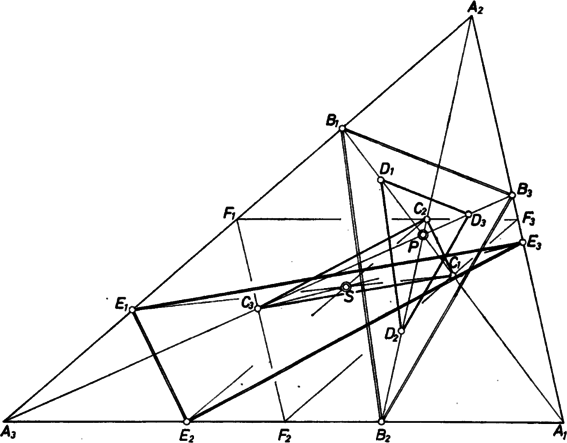1. ábra

A háromszög

t

területének

2 t = a b sin γ

típusú képletét használva,

\frac{2 t}{sin γ}

típusú kifejezéseket fejezünk ki 2‐2 szakasz szorzatával, és fordítva, az átalakítás során kapott szorzatokat ilyen kifejezésekre értelmezünk át. Mindegyik indexre

C_{i}

értelmezése alapján

\begin{matrix} 2 P C_{i} & = P C_{i} + P A_{i} - C_{i} A_{i}, = P C_{i} + P A_{i} - B_{i} C_{i} = \\ = P C_{i} + P A_{i} - (B_{i} P + P C_{i}) = P A_{i} - B_{i} P, \end{matrix}

ennélfogva

1 / sin C_{1} P C_{2} ∢ = k

rövidítéssel, majd felhasználva, hogy

t_{P A_{1} A_{2}} = t_{P A_{1} B_{3}} + t_{P B_{3} A_{2}}

írhatjuk:

\begin{matrix} \frac{8 t_{P C_{1} C_{2}}}{sin C_{1} P C_{2} ∢} = 2 P C_{1} \cdot 2 P C_{2} = (P A_{1} - B_{1} P) (P A_{2} - B_{2} P) = \\ = k \cdot 2 t_{P A_{1} B_{3}} + k \cdot 2 t_{P B_{3} A_{2}} - k \cdot 2 t_{P A_{3} B_{1}} - k \cdot 2 t_{P B_{2} A_{1}} + k \cdot 2 t_{P B_{1} B_{2}}, \end{matrix}

azaz

4 t_{P C_{1} C_{2}}

-t úgy kapjuk, hogy

t_{P B_{1} B_{2}}

-höz hozzávesszük a 2. ábra szerint

+

, ill.

-

jellel jelölt területeket.

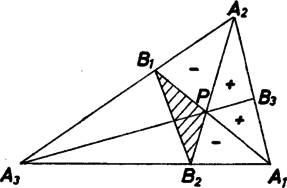2. ábra

Innen az indexek ciklikus permutációjával hasonló kifejezéseket írhatunk fel

4 t_{P C_{2} C_{3}}

-ra és

4 t_{P C_{3} C_{1}}

-re, és e három egyenlőség összegében a 6-6 db

+

és

-

jelű tag összege egyaránt az eredeti háromszög területe. Így továbbalakítással

\begin{matrix} 4 t_{C_{1} C_{2} C_{3}} = t_{B_{1} B_{2} B_{3}} = 4 t_{D_{1} D_{2} D_{3}}, \end{matrix}

hiszen a másik vizsgálandó háromszög,

D_{1} D_{2} D_{3}

B_{1} B_{2} B_{3}

-ból

P

centrumú,

1 / 2

arányú kicsinyítéssel adódik. Ezzel az állítást

P

említett felvételének esetére bebizonyítottuk. Hasonlóan bizonyíthatunk

P

más figyelembe veendő helyzetei mellett is.

II. megoldás. A

D_{1} D_{2} D_{3}

háromszöget a

P

centrumból kétszeresére nagyítva, a

B_{1} B_{2} B_{3}

háromszöget kapjuk. Jelöljük az

A_{1} A_{2} A_{3}

háromszög súlypontját

S

-sel, a

C_{i}

pontnak

S

-re vonatkozó

(- 2)

arányú centrális hasonlóságból származó képét

E_{i}

-vel

(i = 1, 2, 3)

. A feladat állítása nyilvánvalóan ekvivalens azzal, hogy a

B_{1} B_{2} B_{3}

és

E_{1} E_{2} E_{3}

háromszögek területe egyenlő, ezt fogjuk igazolni.
Mivel

C_{1}

rajta van az

F_{2} F_{3}

középvonalon, és ezt a mondott hasonlóság

A_{2} A_{3}

-ba viszi,

E_{1}

rajta van az

A_{2} A_{3}

oldalon. Ezen túlmenően

\begin{matrix} A_{3} E_{1} = 2 F_{3} C_{1} = A_{2} B_{1} \end{matrix}

is igaz, és hasonlóan kapjuk, hogy

E_{2}

A_{1} A_{3}

oldalnak az a pontja, melyre

A_{1} E_{2} = A_{3} B_{2}

E_{3}

pedig az

A_{2} A_{1}

oldalon van, és

A_{2} E_{3} = A_{1} B_{3}

. Mivel az

A_{1} A_{2} A_{3}

B_{1} A_{2} B_{3}

háromszögek egyik szöge közös, területeik aránya megegyezik közös szögükre támaszkodó oldalaik szorzatainak arányával. A

B_{2} A_{3} B_{1}

B_{3} A_{1} B_{2}

háromszögek területét hasonlóan átalakítva, és általában az

X Y Z

háromszög területét

T_{X Y Z}

-vel jelölve kapjuk, hogy

\begin{matrix} \frac{T_{B_{1} B_{2} B_{3}}}{T_{A_{1} A_{2} A_{3}}} & = 1 - \frac{B_{1} A_{2} \cdot A_{2} B_{3}}{A_{1} A_{2} \cdot A_{2} A_{3}} - \frac{B_{2} A_{3} \cdot A_{3} B_{1}}{A_{2} A_{3} \cdot A_{3} A_{1}} - \frac{B_{3} A_{1} \cdot A_{1} B_{2}}{A_{3} A_{1} \cdot A_{1} A_{2}} = \\ = 1 - λ_{1} (1 - λ_{3}) - λ_{2} (1 - λ_{1}) - λ_{3} (1 - λ_{2}), \end{matrix}

ahol

\begin{matrix} λ_{1} = \frac{B_{1} A_{2}}{A_{3} A_{2}}, λ_{2} = \frac{B_{2} A_{3}}{A_{1} A_{3}}, λ_{3} = \frac{B_{3} A_{1}}{A_{2} A_{1}} . \end{matrix}

Mivel

A_{3} E_{1} = A_{2} B_{1}

A_{1} E_{2} = A_{3} B_{2}

A_{2} E_{3} = A_{1} B_{3}

, ugyanazt kapjuk az

E_{1} E_{2} E_{3}

háromszögre is:

\begin{matrix} \frac{T_{E_{1} E_{2} E_{3}}}{T_{A_{1} A_{2} A_{3}}} = 1 - \frac{E_{1} A_{2} \cdot A_{2} E_{3}}{A_{1} A_{2} \cdot A_{2} A_{3}} - \frac{E_{2} A_{3} \cdot A_{3} E_{1}}{A_{2} A_{3} \cdot A_{3} A_{1}} - \frac{E_{3} A_{1} \cdot A_{1} E_{2}}{A_{3} A_{1} \cdot A_{1} A_{2}} = \\ = 1 - (1 - λ_{1}) λ_{2} - (1 - λ_{2}) λ_{3} - (1 - λ_{3}) λ_{1} . \end{matrix}

Ezzel bebizonyítottuk a

B_{1} B_{2} B_{3}

és

E_{1} E_{2} E_{3}

háromszögek területének egyenlőségét.

Megjegyzések. 1. Az

A_{3} E_{1} = A_{2} B_{1}

A_{1} E_{2} = A_{3} B_{2}

A_{2} E_{3} = A_{1} B_{3}

összefüggések azt jelentik, hogy

E_{i}

B_{i}

-nek az

F_{i}

-re vonatkozó tükörképe

(i = 1,2,3)

. Mint megoldásunk második felében beláttuk, ebből következik, hogy tetszőleges

B_{1}

B_{2}

B_{3}

pontok esetén egyenlő a

B_{1} B_{2} B_{3}

E_{1} E_{2} E_{3}

háromszögek területe. Ez az állítás megtalálható példaként Reiman István: Vektorok a geometriában című Középiskolai Szakköri Füzetben (Tankönyvkiadó, Budapest, 1971) a 94. oldalon.
2. Nem használtuk ki lényegesen

P

-nek az

A_{1} A_{2} A_{3}

háromszöghöz képest elfoglalt helyzetét, ezért az állítás a sík bármely

P

pontjából kifejlesztett alakzatra érvényes.
3. Általánosabban is igaz az állítás: Legyen

B_{i}

A_{1} A_{2} A_{3}

háromszög

A_{i}

-vel szemközti oldalának belsõ pontja, az

A_{i} B_{i}

szakaszok felezőpontja

C_{i}

. Ekkor

\begin{matrix} T_{C_{1} C_{2} C_{3}} = \frac{1}{4} T_{B_{1} B_{2} B_{3}}, \end{matrix}

azaz nem szükséges, hogy az

A_{i} B_{i}

szakaszok egy ponton menjenek át.

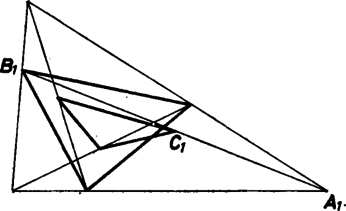3. ábra

Pintér Ferenc (Budapest, Leövey K. Gimn., IV. o. t.)