|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen egy, a föltevés szerinti ötszög . A szimmetriatengely átmegy az egyik csúcson, ugyanis a tükrözés vagy párokba kapcsolja a csúcsokat vagy ‐ ha egy csúcs rajta van a -n ‐ ezt önmagába viszi át. Az ötszög egyik csúcsa az utóbbi típusú, mert az páratlan szám.
Válasszuk úgy a betűzést, hogy az -n menjen át, így merőlegesen felezi a oldalt és a átlót, elég tehát a -nél levő , a -nél levő , valamint az -nál levő szög korlátait vizsgálnunk.
A Gy. 1526 (H) gyakorlatban bebizonyítottuk, hogy a szóban forgó ötszögek mindegyik szöge tompaszög ‐ tekintet nélkül arra, hogy van-e tengelyük ‐ tehát a mindenesetre el nem érhető alsó korlátja mind a három szögnek. Eszerint a szimmetrikus trapézban .
Könnyű látni, hogy és rajta helyzetét, valamint -t és -t megválasztva, megszerkeszthető , majd a -től távolságban haladó egyenesen , vagyis az ötszöget (-t és -t) lényegében egyedül meghatározza. Hasonlóan , az erre tükrös , pontpár és megválasztásával kijelölhető , majd . Végül megválasztása is meghatározza -t és -t: a háromszög fölvétele után -ből érintőt szerkesztünk az körül sugárral rajzolt körhöz (úgy, hogy -t válassza el a körtől), ez adja irányát.
Vezessük be még az , , és jelöléseket, ahol a olda1 -n levő pontja.
A konvexség miatt és . Ekkor fennállnak a következő összefüggések:
Az szög felveheti megengedett legnagyobb értékét, a -ot, mert ekkor , , és , megengedett értékek.
Csökkentve ebben az értékrendszerben -t, vele szigorúan monoton növekszik és is ‐ hiszen szigorúan monoton csökken ‐, másrészt szigorúan monoton csökken, mert szigorúan monoton növekszik; eszerint
Legfeljebb addig csökkenhet , amíg a látott növekedésben eléri a -ot ‐ ha egyáltalán eléri. Elérhető a érték, mert akkor , , és alapján , ezekből , másrészt , megengedett értékek. Ezek szerint hiszen a föntebbieket megfordítva, ezt az értéket és szigorúan monoton csökkenésével érte el (ami a alapján végzett szerkesztésből is kiolvasható); továbbá a talált érték megadja a értéket, hiszen és ‐ mint láttuk egyirányúan változnak: .
Mindezek szerint válaszunk: | |
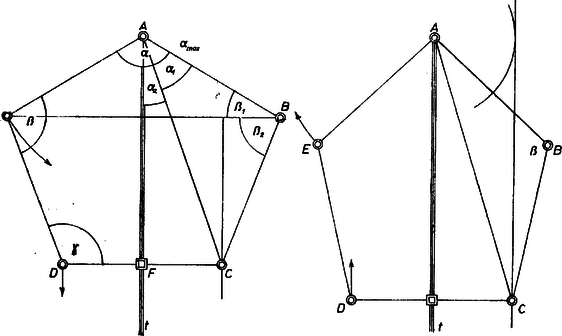
Ábráink mechanikus modellt vázolnak az ötszögről a két szélső helyzetben : az , , csúcsokban csuklók kapcsolják össze az egyenlő oldalakat, a tengelyt realizáló sínen rögzítve van, pedig csúszik, -t állandóan merőleges állásban tartja.
Grafikonunk a szögek változását ábrázolja az magasság függvényében; látjuk, hogy , és egyszerre válik egyenlővé a szabályos ötszög esetében.
Megoldását lásd K.M.L. 49 (1974) 145. |
 PDF |
PDF |  MathML
MathML 
