Kezdőlap


Feladat:	F.1934	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Hornung Tamás
Füzet:	1974/december, 210 - 211. oldal		PDF \| MathML
Témakör(ök):	Középvonal, Szögfelező egyenes, Koszinusztétel alkalmazása, Térgeometriai bizonyítások, Tetraéderek, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1974/április: F.1934

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nem változik meg a felhasznált szögfelezők helyzete akkor ‐ és így a vizsgálandó szögek értéke sem ‐, ha az $A$ , $B$ , $C$ csúcsok bármelyikét eltoljuk $D$ felé (de úgy, hogy ne érje el $D$ -t), vagy az ellentétes irányban. Ezért mindjárt abból indulhatunk ki, hogy $D A = D B = D C = d$ , a gúla mindegyik oldallapja egyenlő szárú háromszög, tehát az $A D B$ , a $B D C$ , a $C D A$ szög felezője átmegy rendre az $A B$ , $B C$ , $C A$ alapélnek $C_{1}$ , $A_{1}$ , illetve $B_{1}$ felezőpontján.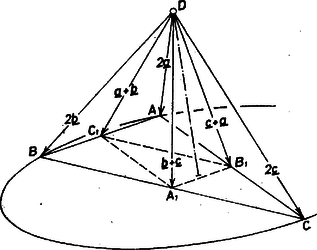

A bizonyítandó állítás így ekvivalens avval, hogy véve az

A_{1} D B_{1}

, a

B_{1} D C_{1}

és a

C_{1} D A_{1}

szögek cosinusát, vagy mind a három érték negatívnak, vagy mind a három pozitívnak, vagy mind a három érték

0

-nak adódik. A

D A_{1} B_{1}

háromszögből, felhasználva, hogy

A_{1} B_{1}

A B C

háromszög középvonala,

A_{1} B_{1} = C_{1} A = A B / 2

\begin{matrix} cos A_{1} D B_{1} ∢ = \frac{D A_{1}^{2} + D B_{1}^{2} - A_{1} B_{1}^{2}}{2 \cdot D A_{1} \cdot D B_{1}} . \end{matrix}

Ennek előjele ugyanaz, mint az

S

számláló előjele, hiszen a nevező pozitív. Mármost

\begin{matrix} S = (D B^{2} - A_{1} B^{2}) + (D C^{2} - B_{1} C^{2}) - C_{1} A^{2} = 2 d^{2} - \frac{1}{4} (B C^{2} + C A^{2} + A B^{2}), \end{matrix}

és ez az előforduló betűkben szimmetrikus. Tehát a

B_{1} D C_{1}

és

C_{1} D A_{1}

szög cosinusának számlálója is

S

, az átfogalmazásunkban szereplő három cosinus érték csak a pozitív nevezőkben különbözik egymástól. Ebből már következik az átfogalmazott állítás, tehát az eredeti állítás is.

II. megoldás. A vektorok skaláris szorzatának alkalmazásával ‐ lényegében az I. megoldás gondolatmenetét követve ‐ még gyorsabban jutunk célhoz.
A

D

csúcsból indítsunk három egyenlő hosszú vektort az

A

B

és

C

csúcsok felé. Jelöljük ezeket rendre

2 a

2 b

2 c

-vel. Mivel

| a | = | b | = | c |

, a feladatban szereplő szögfelezők irányába mutató vektorok

a + b

a + c

és

b + c

. A szögfelezők által bezárt szögek cosinusai:

\begin{matrix} cos B_{1} D C_{1} = \frac{(a+b) (a+c)}{| a+b | \cdot | a+c |}, cos C_{1} D A_{1} = \frac{(a+b) (b+c)}{| a+c | \cdot | b+c |}, \end{matrix}

és

\begin{matrix} cos A_{1} D B_{1} = \frac{(a+c) (b+c)}{| a+c | \cdot | b+c |} . \end{matrix}

A nevezők pozitívok. A számlálókban a beszorzást elvégezve rendre a következő kifejezéseket kapjuk:

\begin{matrix} a^{2}+ab+ac+bc, \\ b^{2}+ab+ac+bc, \\ c^{2}+ab+ac+bc . \end{matrix}

Mivel

a^{2}=b^{2}=c^{2}

, a kapott kifejezések egyenlők, így a feladat állítása az I. megoldás végén mondottak alapján igaz.
Hornung Tamás (Győr, Czuczor G. Bencés Gimn., III. o. t.)