Kezdőlap


Feladat:	F.1920	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1974/október, 66 - 68. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Trigonometriai azonosságok, Háromszögek nevezetes tételei, Terület, felszín, Síkgeometriai számítások trigonometria nélkül, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1974/február: F.1920

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelöljük az $A O C$ szöget $2 x$ -szel ‐ így nyilván elég tekinteni a $0 < x < π / 2$ értékeket ‐, továbbá az $A C$ átmérőjű kört $k_{1}$ -gyel és az $A C$ egyenes $O$ -t nem tartalmazó partján levő $A C$ ívek ‐ ti. a $k$ , illetve $k_{1}$ részét képező ív ‐ felezőpontját $F$ -fel, illetve 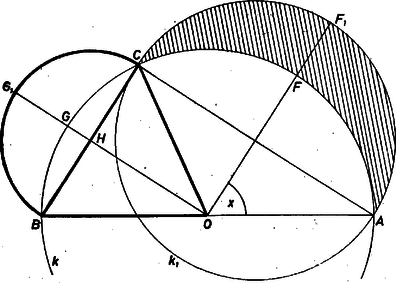$F_{1}$ -gyel.

k_{1}

le nem fedett részének

f (x)

területe egyenlő az

A C F_{1}

félkör és az

A C F

körszelet területének különbségével, a szelet területét pedig az

A O C F

körcikk és az

A O C

egyenlő szárú háromszög területének különbsége adja. Hosszúságegységül

O A

-t választva,

A C = 2 sin x

, a háromszög magassága

cos x

, ezért

\begin{matrix} f (x) = \frac{π}{2} sin^{2} x - (x - sin x \end{matrix}

Ennek szélső értéke ott lehet, ahol a derivált eltűnik:

\begin{matrix} f' (x) = π sin x \end{matrix}

A két ilyen hely közül feladatunk számára egyedül az a hely lényeges, ahol a zárójelbeli kifejezés 0, azaz

\begin{matrix} tg x_{0} = π / 2, x_{0} = 57^{\circ} 31' = 1, 0047 (radián), \end{matrix}

ugyanis a

sin 2 x

tényező az

x = 0

és

x = π / 2

helyeken tűnik el, ekkor

C

A

-ban, illetve

B

-ben van, és így

k_{1}

lefedetlen része 0.
Az

x_{0}

helyen

f (x)

-nek maximuma van, mert az értelmezési tartományban

tg x

növekvő függvény, és így

x < x_{0}

esetén

f' (x) > 0

, ha pedig

x > x_{0}

, akkor

f' (x) < 0

. A maximum értéke egyszerű számítással

\begin{matrix} f (x_{0}) = \frac{π}{2} - x_{0} = 0, 5661. \end{matrix}

(1)

2. A

C

pont kapott helyzetében az

O B C

háromszög területének és a

B C

átmérőjű félkör területének hányadosa

\begin{matrix} \frac{sin x_{0} cos x_{0}}{\frac{π}{2} cos^{2} x_{0}} = \frac{tg x_{0}}{\frac{π}{2}} = 1, \end{matrix}

tehát a két terület valóban egyenlő.

Megjegyzések. 1. Az

f (x_{0}

)-nak (1)-beli kifejezése alapján szemléletesen is bebizonyíthatjuk a feladat állítását. Felhasználhatjuk ebben, hogy az

A C

és

B C

átmérőjű körökből a

k

által le nem fedett részek együttes területe mindig egyenlő az

A B C

háromszög területével, bárhol vesszük is

C

-t a

k

kerületén (az ábra

G

és

G_{1}

pontja a

k

-beli

B C

ív, ill. a

B C

átmérőjű félkörív felezőpontja):

\begin{matrix} A F C F_{1} + B G C G_{1} = A B C, \end{matrix}

(2)

hiszen mindkét oldalhoz hozzáadva az

A C F

és

B C G

körszeletek területét, a jobb oldalon az

A B C

félkör területét kapjuk, ami

(π / 2) {(A B / 2)}^{2} = (π / 8) \cdot A B^{2}

a bal oldal két tagja pedig az

A C

és a

B C

átmérő fölötti félkör területe, ezek összege pedig Pitagorasz tétele alapján ugyancsak

\begin{matrix} \frac{π}{2} {{(\frac{A C}{2})}^{2} + {(\frac{B C}{2})}^{2}} = \frac{π}{8} A B^{2} . \end{matrix}

Felhasználjuk azt is, hogy az

A O C

és

B O C

háromszögek területe egyenlő. Mármost (1) alapján fennáll

\begin{matrix} A F C F_{1} = A B G C F - A O C F = O B G C . \end{matrix}

Hozzáadva mindkét oldalhoz a

B G C G_{1}

holdacskát és figyelembe véve (2)-t, a bal oldal:

\begin{matrix} A F C F_{1} + B G C G_{1} = A B C = 2 \cdot B C O, \end{matrix}

a jobb oldal pedig

\begin{matrix} O B G C + B G C G_{1} = B C G_{1} + B C O, \end{matrix}

amiből

B C G_{1} = B C O

. (A közös

B C

alapon álló félkör és

B C O

háromszög ,,magasságainak'' aránya

H G_{1} : H O = 2 : π

.)
2. A (2) tételt ,,Hippokratész holdacskái'' néven szokás említeni. Hippokratész görög matematikus az i. e. V. században élt. Az a példa, hogy a körívekkel határolt idomok együttes területe egyenlő egy egyenes vonalú idom területével ‐ hosszú időn át táplálta azt a reményt, hogy majd sikerül a körhöz is találni vele egyenlő területi, egyenes vonalú idomot. Ha találtak volna ilyen (körzővel és egyenes vonalzóval szerkeszthető) idomot, akkor már könnyű lenne szerkeszteni vele egyenlő területű négyzetet is ‐ ezt tekintették volna a görögök a területmeghatározás befejezésének. Ma már tudjuk F. Lindemann (1852‐1939) német matematikus bizonyításából, hogy ilyen szerkesztés lehetetlen. (A mi

C

pontunk sem szerkeszthető meg körzővel és vonalzóval; emiatt fogalmazott a szerkesztő bizottság így: ,,határozzuk meg

...

''.)
Ezt a tényt egy nem szerencsés kifejezés bevezetésével magyarul így mondták, illetve mondják: a kör négyszögesítése nehéz probléma, illetve most már lehetetlen. A ,,négyszögesítés'' szó a quadratúra (=területmeghatározás) és quadráció (idommal egyenlő területű négyzet szerkesztése) megfelelője kívánt lenni, de sok hozzá nem értő számárra ‐ sajnálatosan ‐ inkább annak mintegy jelképe lett, hogy a ‐ különben is sokak előtt nem népszerű ‐ matematika milyen hiábavalóságokkal foglalkozik.
Tanulság lehet ebből, hogy idegen szakkifejezések számára csak olyan magyar megfelelőt fogadjunk el, amely a lényeget fejezi ki és nem enged félremagyarázást. Ebben pedig az is nehézség, hogy a hozzáértők beszédében, a gyakori használatban a kifejezések megrövidülnek, másrészt a kérdéssel újonnan ismerkedők (tanulók) részére gyakran mindjárt a rövid kifejezést közlik, kellő ismerkedési, megszokási idő nélkül.