Feladat: F.1838 Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1974/január, 5 - 7. oldal  PDF  |  MathML 
Témakör(ök): Tengely körüli forgatás, Merőleges affinitás, Egyenlő szárú háromszögek geometriája, Hozzáírt körök, Mértani helyek, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):Feladatok: 1972/szeptember: F.1838

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Tekintsük először azt az egyszerű, különleges esetet, ha az F találkozási pont éppen az ABC háromszög síkjában ‐ más néven: a DEC háromszög síkjában ‐ jön létre, ekkor ugyanis a bizonyítás síkmértani feladattá egyszerűsödik. Ekkor mindkét háromszöget 180∘-kal fordítottuk el a találkozásig. Föltevésünk azt jelenti másképpen, hogy C benne van a DEF síkban, tehát vetülete ‐ amit vizsgálnunk kell ‐ önmaga (1. ábra).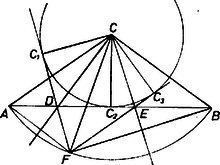

 

 

1. ábra
 

Mivel a háromszög oldalait érintő körök mindegyikének középpontján átmegy a háromszög mindegyik szögének vagy a mellékszögének a felezője, azért elég azt belátnunk az állítás bizonyítására, hogy a DEF háromszög D-beli és E-beli külső szögeinek felezői ‐ vagy hogy ezek egyike és az F-beli belső szögfelező ‐ C-ben metszik egymást, hiszen két szögfelező metszéspontja egyenlő távolságra van mind a három oldal egyenesétől, átmegy rajta a harmadik felező is.
C-nek a DF egyenesen levő C1 vetülete a DF oldal D-n túli meghosszabbításán van, mert a CDF szög mint a CDA szög új helyzete tompaszög, hiszen AD<DB alapján D az AC2 szakaszon van, ahol C2 az AB alap felezőpontja, egyszersmind C vetülete a DE egyenesen. Levonva e két szögből az EDF, illetve C1DA szöget, amelyek egymásnak csúcsszögei, egyenlők a maradó CDE és CDC1 szögek is, eszerint a DC félegyenes valóban felezi az EDC1 külső szöget.
Átadva A itteni szerepét B-nek, D-ét pedig E-nek, kapjuk, hogy EC felezi a DEF szög külső (mellék-) szögeit, tehát C valóban középpontja a mondott külső érintő körnek.
(Feltűnőbben használjuk ki a CA=CB egyenlőséget, ami az F pont létrejöttének szükséges föltétele, a következő egyenlőségláncolatban:
CFD∢=CAD∢=CAB∢=CBA∢=CBE∢=CFE∢,
tehát FC felezi a DFE belső szögét a DEF háromszögnek.)
b) A már elintézett esetet kizárva, F két helyzetben adódik ‐ a háromszögeket a vízszintesnek gondolt ABC sík fölé, illetve alá fordítva. Mivel azonban az így létrejött két alakzat egymás tükörképe az ABC síkra nézve, elég a sík egyik oldalán létrejött F helyzettel foglalkoznunk. Könnyebb elképzelés érdekében úgy fordítjuk el alakzatunkat az AB egyenes mint tengely körül, hogy a DEF sík álljon vízszintesen (2. ábra).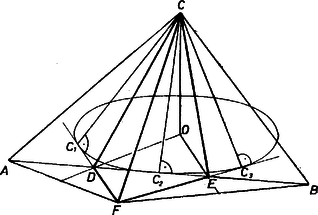
 

 

2. ábra
 

Körünk O középpontját ismét az EDC1 és DEC3 külső szögeket felező egyenesek metszéspontjaként tekintjük előállítva, ahol C3 a C vetülete az EF egyenesen. A DO egyenes felezi a szög ADF csúcsszögtartományát is, így pedig egyben magasságvonala is az AFD háromszögnek, hiszen ez egyenlő szárú, alakzatunk előállításánál fogva: DF=DA. Ugyancsak az előállításnál fogva CF=CA. Ezek szerint O, D és C az AF szakasz felező merőleges síkjának pontjai, és ez a sík merőleges az AF-et tartalmazó DEF síkra.
Meggondolásunkban D és A (és C1) szerepét rendre E-nek, B-nek (C3-nak) átadva, O, E és C a BF szakasz felezőmerőleges síkjának pontjai, és e sík szintén merőleges a DEF síkra. Ennélfogva a két felező merőleges sík OC metszésvonala is merőleges a DEF síkra, tehát O a C-nek e síkon levő merőleges vetülete. Ezzel az állítást bebizonyítottuk. (Kihasználtuk azt is, hogy a két sík különböző, mert D és E különbözők, és O nincs rajta DE-n, így tehát OC-re a DEF síkban két különböző, rá merőleges egyenest találtunk: OD-t és OE-t.)
A feladat szövegének harmadik mondatában szereplő ,,találkozott'' igealakot úgy értelmezzük, hogy a DEF háromszög létrejött; emiatt nem diszkutáltuk a D és E megválasztási lehetőségei és F létrejötte közti kapcsolatot.
 

Megjegyzések. 1. Könnyű látni, hogy az a) esetben az ACD és BCE szögek összege éppen egyenlő a DCE szöggel, a b) esetben pedig nagyobb nála; ekkor létrejön a C csúcsú CDEF testszöglet (triéder). Az
ACD∢+BCE∢>DCE∢
feltétel a feladat eredeti, AD<DB, AE>EB feltételeivel együtt elegendő is a triéder létrejöttéhez, hiszen így
ACD∢<DCE∢+BCE∢ésBCE∢<DCE∢+ACD∢.

2. O-nak a DEF háromszög belsejéhez képest elfoglalt helyzetéből némi (egyenlőtlenséges) következtetést vonhatunk le a CDEF gúlában a DEF alaplap és a C-ben összefutó oldallapok közti lapszögekre vonatkozóan: az FD, FE alapélű oldallapok hegyesszöget alkotnak az alaplappal, a DE élnél viszont tompaszög van. Az utóbbi abból is adódik, hogy a CA, CB éleknek CF-fé egyesítése után F-nek az ABC háromszög síkján levő vetülete az AB-nek C-t nem tartalmazó oldalára esik.
 

II. megoldás. Jelöljük a kérdéses külső érintő körnek a DE, EF, FD egyenesen levő érintési pontját ‐ más szóval O-nak az egymás utáni egyenesekre való vetületeit ‐ rendre G, H, K betű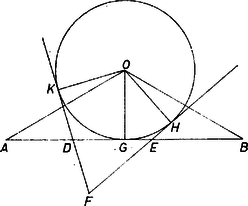vel.
 

 

3. ábra
 

A körhöz a D és E pontokból húzott érintőszakaszok egyenlősége alapján (3. ábra):
FK=FD+DK=FD+DG=AD+DG=AG,FH=FE+EH=FE+EG=BE+EG=BG,


és mivel még FK=FH is áll, azért AG=BG. Eszerint G az AB szakasz felezőpontja, ami egyszersmind C-nek az AB, azaz DE egyenesen levő vetülete. S mivel így GC is, GO is merőleges AB-re, azért a COG sík is merőleges rá, ennélfogva a DEF síkra is.
Amikor a CAD háromszöget a CFD helyzetbe elfordítjuk, fordítsuk vele síkjának G pontját is, vagyis a CAG háromszöget. Így DG=DK alapján G a K-ba jut, CG a CK-ba, és az előbbihez hasonlóan a COK sík is merőleges a DEF síkra. Ekkor pedig ugyanez áll CO metszésvonalukra is, tehát O valóban vetülete a C-nek a DEF síkon, ezt kellett bizonyítanunk.