Feladat: F.1792 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bálint L. ,  Bara T. ,  Bartha M. ,  Bezdek K. ,  Bodnár I. ,  Breuer Péter ,  Burda Magdolna ,  Császár Gy. ,  Éber N. ,  Gál P. ,  Gáspár Gy. ,  Gyenese T. ,  Hargitai B. ,  Józsa I. ,  Kémeri Viktória ,  Kertész Á. ,  Kiss E. ,  Kollár István ,  Kószó K. ,  Kovács I. ,  Lakner P. ,  Lámer G. ,  Lang I. ,  Meszéna G. ,  Nagy Sándor ,  Nagy Zoltán ,  Naumann L. ,  Pach J. ,  Pataki B. ,  Pintér F. ,  Sebő A. ,  Stachó B. ,  Stépán G. ,  Szigeti G. ,  Tari J. ,  Tóth K. ,  Turán Gy. ,  Vida T. ,  Wettl F. 
Füzet: 1972/október, 56 - 58. oldal  PDF  |  MathML 
Témakör(ök): Trigonometrikus egyenletrendszerek, Paraméteres egyenletrendszerek, Parabola egyenlete, Mértani helyek, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):Feladatok: 1971/november: F.1792

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen rövidítésül

sinnx=ξ,(3)cosny=η.(4)
Ekkor
ξη=12{(ξ+η)2-(ξ2+η2)}=v2-u2,
tehát ξ és η a következő másodfokú egyenlet gyökei:
(z-ξ)(z-η)=z2-(ξ+η)z+ξη=z2-vz+v2-u2=0.(5)



Innen akkor és csak akkor kapunk olyan megoldást, amely mellett (3) és (4) egyidejűleg megoldást ad x-re, és y-ra, ha (5) mindkét gyöke valós és fennáll
n=2kesetén  0≤ξ,η≤1,(6a)n=2k+1  esetén  -1≤ξ,η≤1,(6b)
hiszen bármely x,y szám sinusa és cosinusa -1 és 1 közé eső szám, és n-edik hatványuk n páros vagy páratlan volta szerint 0 és 1 közé, ill. -1 és 1 közé esik ‐ a két határt mindig megengedve.
Mivel (5)-ben a másodfokú tag együtthatója pozitív, azért az
f(z)=z2-vz+v2-u2=(z-v2)2+v2-2u4
függvénynek minimuma van a v2 helyen, és ennek értéke v2-2u4. Ismeretes, hogy (5) gyökei akkor és csak akkor valósak, ha e minimum nem pozitív:
v2-2u≤0,v2≤2u.(7)

Annak szükséges és elegendő feltételei pedig, hogy (6a), ill. (6b) teljesüljön a gyökökre:

egyrészt, hogy a minimum helye a (0, 1), ill. (-1, 1) intervallumban legyen:
0≤v2≤1,azaz  M0≤v≤2,ill.(8a)-1≤v2≤1,azaz  -2≤v≤2,(8b)
másrészt hogy az intervallum mindkét végpontjában f(z) értéke már nem negatív legyen. Eszerint minden n-re
f(1)=1-v+v2-u2=12{(v-1)2-(u-1)|}≥0,  azaz(v-1)2≥(u-1),(9)


továbbá n párossága szerint
f(0)=v2-u2≥0,azazv2≥u,ill.(10a)f(-1)=12{(v+1)2-(u-1)}≥0,azaz(v+1)2≥u-1.(10b)

2. Az eddigiek szerint a kívánt tulajdonságú P(u,v) pontok koordinátáinak minden n esetén teljesíteniük kell a (7) és (9) feltételeket, továbbá páros n esetén a (8a), (l0a) feltételpárt, páratlan n esetén pedig a (8b), (10b) párt; és fordítva, ha adott n esetén egy P pont koordinátái teljesítik a megfelelő négy feltételt, ez elegendő is ahhoz, hogy az (1), (2) rendszernek legyen megoldása, ekkor tehát P hozzátartozik a mértani helyhez.
Mármost (8a) és (8b) egy-egy az x tengellyel párhuzamos síksávot jelölnek ki. ‐ Ha (10a) az egyenlőség jelével teljesül, akkor P a v2=u egyenletű parabolán van rajta, vagyis azon, melynek csúcsa az origó, fókusza az (14,0) pont; ha pedig a bal oldal nagyobb ‐ ahol az ordináta áll ‐, akkor a parabola külsejében van P, vagyis a parabolavonal által kettévágott síknak a fókuszt nem tartalmazó részében. ‐ Akkor is parabolán van P, ha (9), ill. (10b) teljesül az egyenlőség jelével, ezek az előbbiből azzal az eltolással adódnak, amely csúcsát az (1, 1), ill. (1, -1) pontba viszi; egyenlőtlenség esetén pedig ismét a megfelelő parabola külsejéről van szó.
Végül hasonlóan (7) az origó csúcsú és (12,0) fókuszú parabola vonalán és a belsejében levő pontokra és csak ezekre teljesül.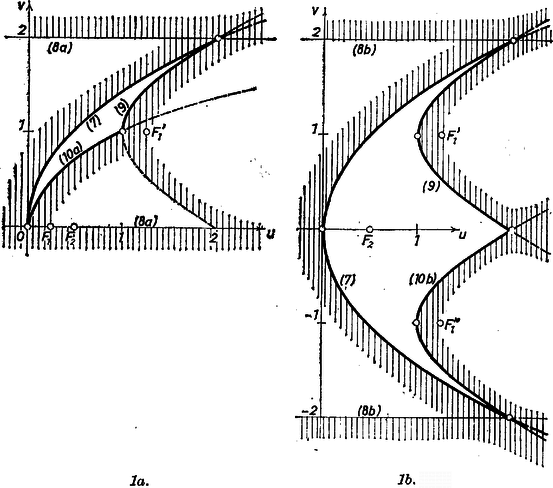
 

 

Az 1a ábrán páros n-ekre, az 1b ábrán páratlanokra tüntettük fel a megfelelő sávhatár-egyeneseket, parabolákat, és mellettük vonalkázással jelöltük a keletkezett síkrészek közül azokat, amelyek pontjai nem teljesítik az illető feltételt. Így a mind a négy feltételt teljesítő síkrész jelöletlenül, fehéren maradt, ez és a határvonala adja a keresett mértani helyet.
 

Breuer Péter (Eger, Gárdonyi G. Gimn., IV. o. t.)

Kollár István (Budapest, Móricz Zs. Gimn., IV. o. t.)