Kezdőlap


Feladat:	F.1787	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Holló Mihály
Füzet:	1972/április, 153 - 154. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Geometriai egyenlőtlenségek, Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1971/október: F.1787

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Válasszuk hosszúságegységnek az alapél felét, legyen a gúla magassága $O E = m$ (az adott $A E : A B = 2$ aránytól egyelőre eltekintve) és 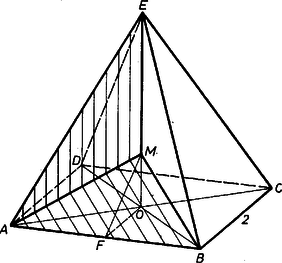$O M = x$ $(> 0)$ .

1. ábra

Így, az

A B

él felezőpontját

F

-fel jelölve

F M = \sqrt[]{x^{2} + 1}

, másrészt

A O = \sqrt[]{2}

, és a vizsgálandó területösszeg (1. ábra)

\begin{matrix} t (x) = A F \cdot F M + \frac{1}{2} M E \cdot A O = \sqrt[]{x^{2} + 1} + \frac{m - x}{\sqrt[]{2}}, \end{matrix}

0 < x \leq m

. Ennek deriváltja

\begin{matrix} t' (x) = \frac{x}{\sqrt[]{x^{2} + 1}} - \frac{1}{\sqrt[]{2}} = \frac{1}{\sqrt[]{1 + \frac{1}{x^{2}}}} - \frac{1}{\sqrt[]{1 + 1}}, \end{matrix}

és ez csak akkor tűnik el, ha

\frac{1}{x^{2}} = 1

x = 1

, csak itt lehet szélső érték, amennyiben

x = 1

beletartozik az értelmezési tartományba ‐ ti.

A E / A B = 2

, azaz

A E = 4

esetén is.
Látható, hogy ha

0 < x < 1

, akkor

t' (x) < 0

, ha pedig

x > 1

, akkor

t' (x) > 0

. Másrészt

A E = 4

esetén

m = \sqrt[]{14} > 1

, ezek szerint

x = 1

-ben minimuma van a területösszegnek.

II. megoldás. Alakítsuk

t (x)

fenti első kifejezését így: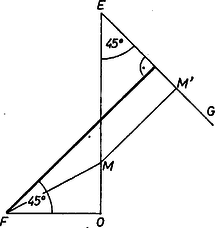

\begin{matrix} t (x) = A F (F M + \frac{M E}{\sqrt[]{2}}), \end{matrix}

Mivel

A F

állandó, eszerint

x

-et úgy kell megválasztanunk, hogy a zárójelbeli két szakasz összege a lehető legkisebb legyen. Szemléletes jelentést adhatunk ennek a feladatnak a gúla

F O E

síkmetszetében. Rajzoljunk

E

-n át az

E O

magassággal

45^{\circ}

-os szöget bezáró

E G

félegyenest az

F

-et nem tartalmazó oldalon, és legyen ezen

M

vetülete

M'

(

2

. ábra).

2. ábra

A zárójel második tagja nyilvánvalóan

M M'

, és a két tag összege az

F

-től

E G

-ig megtett utunk, ha

E O

-ig is és tovább

E G

-ig is egyenesen haladunk, az utóbbi részben

E G

-re merőlegesen. Ez az út nyilvánvalóan akkor a legrövidebb, ha

O E

átlépésekor nem változtatunk irányt,

O F M ∢ = 45^{\circ}

, tehát ha

O M = O F = 1

Holló Mihály (Budapest, I. István Gimn., III. o. t)

Megjegyzés. Az utóbbi megoldásban alkalmazott módszer eredményesen használható a következő feladatban is. Adott a síkban egy

e

egyenes, továbbá rajta egy

B

és kívül egy

A

pont. Határozzuk meg

e

-nek azt a

P

pontját, melyre a

\begin{matrix} λ \cdot A P + μ \cdot P B \end{matrix}

összeg minimális, ahol

λ

μ

tetszőleges pozitív számok.