Kezdőlap


Feladat:	F.1774	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Tibor , Vigassy Lajos
Füzet:	1972/május, 197 - 200. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Harmadfokú (és arra visszavezethető) egyenletek, Középpontos és egyéb hasonlósági transzformációk, Parabola egyenlete, Kúpszeletek érintői, Síkbeli ponthalmazok távolsága, Feladat
Hivatkozás(ok):	Feladatok: 1971/május: F.1774

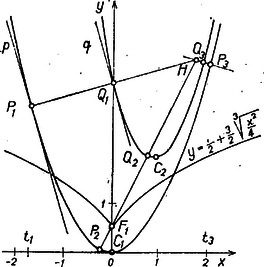
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel, hogy a feladat kérdésére a válasz igenlő, a $p$ parabola $t$ abszcisszájú $P (t, t^{2})$ pontja és a $q$ parabola $Q (u,2 u^{2} - 7 u / 2 + 57 / 16)$ pontja teljesíti a követelményt. Ekkor $p$ -nek $P$ -beli és $q$ -nak $Q$ -beli érintője párhuzamos egymással.

Mivel e két görbe esetében az ordináta az abszcisszának differenciálható függvénye, azért az érintő iránytangensét megadja a deriváltnak az illető helyen fölvett értéke,

p

és

P

esetében

2 t

q

és

Q

esetében

4 u - 7 / 2

, és e kettő egyenlő egymással:

\begin{matrix} 2 t = 4 u - 7 / 2, t = 2 u - 7 / 4. \end{matrix}

(1)

Másrészt a

P Q

egyenes merőleges mindkét érintőre ‐ más szóval

P Q

a két parabola közös normálisa ‐ eszerint

q

-nak

Q

-beli normálisa átmegy a

P

ponton. E normális iránytényezője

- 1 / (4 u - 7 / 2)

, hacsak a nevező

0

-tól különböző ‐ azaz

u \neq 7 / 8

‐tehát egyenlete

\begin{matrix} y - (2 u^{2} - \frac{7}{2} u + \frac{57}{16}) = \frac{- 1}{4 u - 7 / 2} (x - u), \end{matrix}

(2)

és ezt

P

koordinátái kielégítik. Ezeket (1) alapján mindjárt

u

-val kifejezve,

u

-ra kapunk egyenletet:

\begin{matrix} {(2 u - \frac{7}{4})}^{2} - 2 u^{2} + \frac{7}{2} u - \frac{57}{16} = \frac{- 1}{4 u - 7 / 2} (u - 7 / 4), \end{matrix}

\begin{matrix} 8 u^{3} - 21 u^{2} + \frac{45}{4} u = 8 u (u^{2} - \frac{21}{8} u + \frac{45}{32}) = 8 u (u - \frac{15}{8}) (u - \frac{3}{4}) = 0. \end{matrix}

(3)

Eszerint

u

, majd (1) alapján

t

megfelelő értékei, végül a követelményt kielégítő

P

Q

pontpárok a következők (oszlopokba rendezve):

\begin{matrix} u_{1} = 0 & u_{2} = \frac{3}{4} & u_{3} = \frac{15}{8} \\ t_{1} = - \frac{7}{4} & t_{2} = - \frac{1}{4} & t_{3} = 2 \\ P_{1} (- \frac{7}{4}; \frac{49}{4}) & P_{2} (- \frac{1}{4}; \frac{1}{16}) & P_{3} (2; 4) \\ Q_{1} (0; \frac{57}{16}) & Q_{2} (\frac{3}{4}; \frac{33}{16}) & Q_{3} (\frac{15}{9}; \frac{129}{32}) \end{matrix}

Megjegyzés.

P_{i}

Q_{i}

(i = 1,2,3)

pontpárok pontos megadása azon múlott, hogy a (3) harmadfokú egyenletnek

u = 0

gyökét felismertük. Ha

t

helyett

u

-t küszöböltük volna ki, akkor nem állt volna elő ez a szerencsés helyzet. Hasznos tehát néha az efféle próbálkozás.

II. megoldás (vázlat). Bármely két parabola,

v_{1}

és

v_{2}

, hasonló egymáshoz (alakra nézve), hiszen egyetlen lineáris adatuk, a

p_{1}

, ill.

p_{2}

paraméterük meghatározza őket,

v_{1}

-et

λ = p_{2} / p_{1}

arányban nagyítva és kellően elmozdítva

v_{2}

-t kapjuk. A transzformációban az

F_{1}

, ill.

F_{2}

fókuszok és a

C_{1}

, ill.

C_{2}

csúcsok természetesen egymásnak felelnek meg páronként. Továbbá

v_{1}

-ből egy tetszőleges

A_{1}

pontnak

v_{2}

-beli megfelelőjét,

A_{2}

az a félegyenes metszi ki, amely

F_{2}

-ből indul és amelyre a

C_{2} F_{2} A_{2}

szög nagyság és forgási irány szempontjából egyenlő a

C_{1} F_{1} A_{1}

szöggel.
Amennyiben még a két parabola tengelyei párhuzamosak (és síkjuk közös), az

A_{2}

-beli érintő párhuzamos az

A_{1}

-beli érintővel, ekkor

v_{1}

és

v_{2}

centrális hasonlósági helyzetben vannak egymáshoz képest ‐ hacsak

C_{1} F_{1} F_{2} C_{2}

nem paralelogramma ‐, a hasonlóság centruma az

F_{1} F_{2}

C_{1} C_{2}

egyenespár

H

metszéspontja. (A kiemelt esetben pedig transzlációval vihető át egymásba

v_{1}

és

v_{2}

).
Esetünkben fordítva, olyan

P

Q

pontpárt keresünk a párhuzamos tengelyű

p

q

parabolapáron, amelyekben az érintők párhuzamosak. Ezért

P

Q

a hasonlóságban megfelelő pontpár, ugyanis a parabolához bármely iránnyal párhuzamosan egy és csakis egy érintő illeszthető. Így a

P Q

egyenes átmegy

H

-n. Ezek alapján tervünk a következő: kiszámítjuk

H

koordinátáit, felírjuk

q

-nak

u

abszcisszájú

Q

pontjában az érintőre merőleges

n

egyenes ‐ a fenti normális ‐ egyenletét, ekkor

u

-ra abból kapunk egyen1etet, hogy

H

koordinátái kielégítik

n

egyenletét.
Mármost az adott

p

parabola

C_{1}

csúcsa az origó, paramétere

p_{1} = 1 / 2

. Hasonlóan

q

egyenletét kellően alakítva:

\begin{matrix} {(x - \frac{7}{8})}^{2} = \frac{1}{2} (y - \frac{65}{32}), \end{matrix}

tehát csúcsa:

C_{2} (\frac{7}{8}, \frac{65}{32})

,paramétere:

p_{2} = \frac{1}{4}

. Így a

q

parabola

p_{2} / p_{1} = 1 / 2

arányú kicsinyítéssel áll elő

p

-ből,

C_{2}

felezi a

C_{1} H

szakaszt, más szóval

H

C_{1}

-nek

C_{2}

-re vonatkozó tükörképe:

H (\frac{7}{4}, \frac{65}{16})

Ezt a fenti (2)-be helyettesítve és rendezve

\begin{matrix} (\frac{65}{16} - 2 u^{2} + \frac{7}{2} u - \frac{57}{16}) (4 u - \frac{7}{2}) + (\frac{7}{4} - u) = 0, 8 u^{3} - 21 u^{2} - \frac{45}{16} u = 0, \end{matrix}

mint az I. megoldásban.

Megjegyzések. 1. A fenti (2) mintájára az

y = x^{2}

normálparabola

(u, u^{2})

pontjában a normális egyenlete

x + 2 u y - (2 u^{3} + u) = 0

, ill.

u

szerint rendezve

2 u^{3} - (2 y - 1) u - x = 0

(ez az alak már

u = 0

esetén is érvényes). Ennek harmadfokú volta azt jelenti, hogy tetszés szerint választva egy

P (x, y)

pontot, ehhez három olyan

(u, u^{2})

pontja tartozik a normálparabolának, amelynek normálisa átmegy

P

-n. Ezt így szokás mondani: bármely parabola összes normálisait véve, ezek harmadosztályú görbesereget alkotnak, a sík bármely pontján három megy át a sereg egyenesei közül. Hozzá kell azonban tennünk ehhez, hogy szemléletesen csak akkor igaz ez, ha a harmadfokú egyenlet

u

-ra három egymástól különböző, valós gyököt szolgáltat. Felírva a gyököket az iskolai függvénytáblázat^{$^{*}$} 251. 31 ‐ 32 képletei szerint, akkor és csak akkor, kapunk ilyen három gyököt, ha

\begin{matrix} {(- \frac{x}{2})}^{2} - {(\frac{2 y - 1}{3})}^{3} < 0, azaz y > \frac{1}{2} (1 + 3 \sqrt[3]{\frac{x^{2}}{4}}), \end{matrix}

más szóval, ha

P

,,fölötte'' van az

y = (1 + 3 \sqrt[]{x^{2} / 4}) / 2

egyenletű vonalnak (lásd az ábrát). ‐ Esetünkben

q

hasonló görbéjét is figyelembe kell venni.
2. A fentiek szerint

P_{i} (i = 1,2,3)

p

-nek és

Q_{i}

q

-nak olyan ponthármasa, amelyekben megrajzolt normálisok egy pontban (

H

-ban) metszik egymást. Éppen ennek feltételét állapítottuk meg az 1770. feladatban;^{$^{*}$} a

P_{1} P_{2} P_{3}

háromszög súlypontjának

p

tengelyén, az

x = 0

egyenesen kell lennie, a

Q_{1} Q_{2} Q_{3}

háromszög súlypontjának pedig

q

tengelyén, az

x = \frac{7}{8}

egyenesen. Valóban,

(t_{1} + t_{2} + t_{3}) = 0

és

(u_{1} + u_{2} + u_{3}) / 3 = 7 / 8

.
3. Az ábra szemlélete azt sejteti, hogy ha

p

-t és

q

-t egy térképen egy folyó két partjának tekintjük, akkor a folyó a

P_{3} Q_{3}

normálisszakasz mentén a legszűkebb, hasonlóan a

P_{1} Q_{1}

szakasz egy bizonyos környezetében szintén mindenütt szélesebb a

P_{1} Q_{1}

szakasznál, végül

P_{2} Q_{2}

-nek egy környezetében a

P_{2} Q_{2}

szakasz a legnagyobb szélesség. ‐ A kérdés vizsgálatához az iskolai ismeretanyag nem elegendő. Azoknak, akik a kérdéssel foglalkozni akarnak, a következő két ötletet adjuk. Definiálni kellene, mit értsünk

q

-nak egy, a

p

-n felvett

P

ponthoz legközelebbi

Q

pontján. Vajon igaz-e, hogy

P Q

mindig átmegy a fenti

H

hasonlósági centrumon?

^{$^{*}$}Hack F.‐ Kugler S.-né: Függvénytáblázatok, Matematikai és fizikai összefüggések. Tankönyvkiadó. Budapest. 1968.

^{$^{*}$}Lásd a megoldást K. M. L. 43 (1971) 56.