Kezdőlap


Feladat:	F.1772	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Grácin Edit
Füzet:	1972/január, 10 - 11. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Súlypont, Két pont távolsága, szakasz hosszúsága, Térgeometria alapjai, Feladat
Hivatkozás(ok):	Feladatok: 1971/április: F.1772

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Fel fogjuk használni, hogy az $x$ , $y$ , $z$ oldalakkal szerkesztett háromszög $x$ oldalához tartozó $s_{x}$ súlyvonal négyzete ‐ mint alább megmutatjuk ‐ $s_{x}^{2} = (2 y^{2} + 2 z^{2} - x^{2}) / 4$ , másrészt, hogy a súlypont távolsága az $y$ és $z$ oldalak közös végpontjától 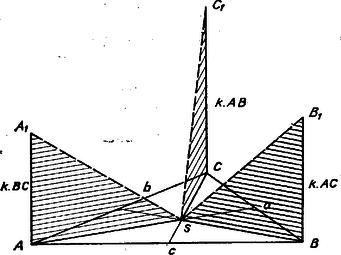$2 s_{x} / 3$ .
Legyen az $A B C$ háromszög súlypontja $S$ , oldalainak hossza $B C = a$ , $C A = b$ , $A B = c$ (1. ábra).

1. ábra

Így az

S A_{1} = S B_{1}

követelményből

S A^{2} + A A_{1}^{2} = S B^{2} + B B_{1}^{2}

, azaz

\begin{matrix} \frac{2 b^{2} + 2 c^{2} - a^{2}}{9} + k^{2} a^{2} = \frac{2 c^{2} + 2 a^{2} - b^{2}}{9} + k^{2} b^{2}, \end{matrix}

rendezve

\begin{matrix} k^{2} (a^{2} - b^{2}) = \frac{a^{2} - b^{2}}{3}, \end{matrix}

ennek

a \neq b

esetén csak

k = 1 / \sqrt[]{3}

felel meg (

k > 0

a = b

esetén pedig bármely pozitív

k

A talált

k

értékkel

\begin{matrix} S A_{1}^{2} = S B_{1}^{2} = \frac{2}{9} (a^{2} + b^{2} + c^{2}), \end{matrix}

és ugyanekkora hasonlóan

S C_{1}^{2}

is. Tehát

k = 1 / \sqrt[]{3}

az egyetlen megfelelő érték, ha az

A B C

háromszögnek van két különböző oldala, ha pedig a háromszög szabályos, akkor nyilvánvalóan bármely

k

érték megfelel. A kérdéses távolság

\begin{matrix} \frac{1}{3} \sqrt[]{2 (a^{2} + b^{2} + c^{2})} . \end{matrix}

A felhasznált képlet levezethető ebből: a

K L M N

paralelogramma oldalainak négyzetösszege egyenlő átlóinak négyzetösszegével (2. ábra).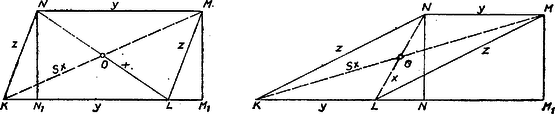

2. ábra

Legyen

L K N ∢ \leq 90^{\circ}

és

N

M

vetülete a

K L

egyenesen

N_{1}

M_{1}

, így

K N_{1} = L M_{1}

és

M M_{1} = N N_{1}

, tehát

K M^{2} + L N^{2} = {(K L + L M_{1})}^{2} + M M_{1}^{2} + {(K L - K N_{1})}^{2} + N N_{1}^{2} = 2 K L^{2} + 2 (L M_{1}^{2} + M M_{1}^{2}) = K L^{2} + M N^{2} + L M^{2} + N K^{2}

.
Ha ugyanis még az oldalak

K L = M N = y

K N = L M = z

, az átlók metszéspontja

O

, akkor

K O = s_{x} = K M / 2

K L N

háromszög

L N = x

oldalához tartozó súlyvonal, és

4 s_{x}^{2} + x^{2} = 2 y^{2} + 2 z^{2}

, ebből fejeztük ki fönt

s_{x}

-et.

Grácin Edit (Szeged, Radnóti M. Gimn., III. o. t.)