Kezdőlap


Feladat:	F.1753	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Angyal J. , Bacsó G. , Balog J. , Balogh Z. , Boros E. , Engedi A. , Ferró J. , Földes T. , Földvári Cs. , Gál P. , Gáspár Gy. , Glódy A. , Golda J. , Hanák G. , Kelen M. , Kertész Á. , Lámer G. , Nagy Sándor (Bp. Apáczai) , Nagy Sándor (Bp. I. István) , Pásztor M. , Pataki B. , Petz D. , Pintér I. , Polyák G. , Poór Zs. , Reviczky J. , Rudas T. , Szász Gy. , Székely A. , Szeredi J. , Umáthum J. , Vályi G.
Füzet:	1972/május, 195 - 197. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Középpontos és egyéb hasonlósági transzformációk, Hozzáírt körök, Feuerbach-kör, Súlypont, Magasságpont, Feladat
Hivatkozás(ok):	Feladatok: 1971/január: F.1753

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az eredeti háromszögbe beleírt és a köréje írt kör középpontját $K^{*}$ -gal, illetve $L^{*}$ -gal, a háromszög súlypontját $S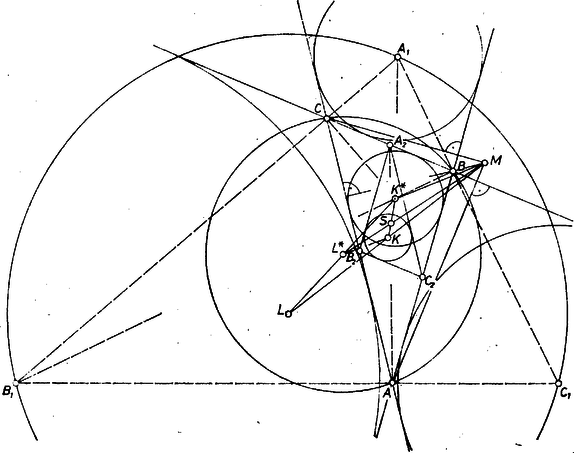$ -sel.

1. ábra

Azt fogjuk bizonyítani, hogy (1. ábra)
a)

L^{*}

felezi a

K^{*} L

szakaszt,
b)

S

L^{*} M

szakasz

L^{*}

-hoz közelebbi harmadolópontja,
c)

S

K K^{*}

szakasz

K

-hoz közelebbi harmadolópontja.
A b) és c) állítás szerint

K L^{*} ∥ K^{*} M

és

{K L}^{*} = K^{*} M / 2

, hiszen a

K L^{*} S

és

K^{*} M S

háromszögek hasonlók, és megfelelő oldalaik aránya

K S : S K^{*} = 1 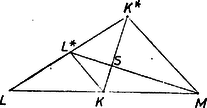: 2

(2. ábra).

2. ábra

Eszerint a

K^{*} L^{*}

és

M K

egyenesek metszik egymást, és

L'

metszéspontjukra teljesül, hogy

L^{*}

felezi az

L' K^{*}

szakaszt és

K

felezi az

L' M

szakaszt. Mivel az első tulajdonság csak

K^{*}

-nak

L^{*}

-ra vonatkozó tükörképére teljesülhet, és a) szerint

L

-nek megvan ez a tulajdonsága,

L

azonos

L'

-vel, tehát

K

felezi az

L M

szakaszt, amint azt bizonyítani akarjuk.
Elegendő tehát az a), b), c) állításainkat bebizonyítanunk. Ehhez fel fogjuk használni a következő két állítást (3‐4. ábra):
I. Egy

H_{0} = A_{0} B_{0} C_{0}

háromszögben a csúcsoknak a szemközti oldalakon levő

A_{1}

B_{1}

C_{1}

vetületei, és a

B_{0} C_{0}

C_{0} A_{0}

A_{0} B_{0}

szakaszok

A_{2}

B_{2}

C_{2}

felezőpontjai rajta vannak egy

k_{0}

körön, amelynek

F_{0}

középpontja az

L_{0} M_{0}

szakasz felezőpontja, ahol

M_{0}

H_{0}

magasságpontja,

L_{0}

a köréje írt kör középpontja,

S_{0}

pedig

H_{0}

súlypontja.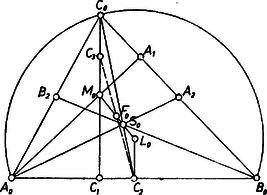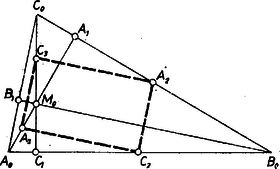

3. ábra

4. ábra

II. A

H_{0}

háromszög

S_{0}

súlypontja az

L_{0} M_{0}

szakasz

L_{0}

hoz közelebbi harmadolópontja.
Az I. állításban szereplő

k_{0}

kört a

H_{0}

háromszög Feuerbach-féle körének, az

M_{0}

S_{0}

L_{0}

pontokon átmenő egyenest pedig a háromszög Euler-féle egyenesének nevezzük. Állításaink bizonyítása sok helyen megtalálható ugyan, az azonban olyan egyszerű, hogy érdemes itt megismételni.
I. Jelöljük az

A_{0} M_{0}

B_{0} M_{O}

C_{0} M_{0}

szakaszok felezőpontját rendre

A_{3}

-mal,

B_{3}

-mal,

C_{3}

-mal. Az

A_{0} B_{0} M_{0}

háromszögnek

A_{3} C_{2}

középvonala, ez a szakasz tehát fele akkora, mint az

M_{0} B_{0}

szakasz, és párhuzamos vele. Ugyanígy kapjuk, hogy

C_{3} A_{2}

is az

M_{0} B_{0}

-nak,

A_{3} C_{3}

és

C_{2} A_{2}

pedig az

A_{0} C_{0}

szakasznak felére kicsinyített képe. Mivel pedig

M_{0} B_{0}

merőleges

A_{0} C_{0}

-ra, azért ezekből következik, hogy az

A_{2} C_{3} A_{3} C_{2}

négyszög téglalap, tehát az

A_{2} A_{3}

C_{2} C_{3}

szakaszok feletti Thalész-körök azonosak. Ugyanígy láthatjuk be, hogy az

A_{2} A_{3}

és

B_{2} B_{3}

feletti Thalész-körök is azonosak, tehát van olyan

k_{0}

kör,amely az

A_{2}

B_{2}

C_{2}

A_{3}

B_{3}

C_{3}

pontok mindegyikén átmegy, legyen ennek a középpontja

F_{0}

.
Mivel az

A_{2} A_{3}

szakasz

A_{1}

-ből derékszög alatt látszik,

A_{1}

is rajta van

k_{0}

-on, és ugyanígy

B_{1}

és

C_{1}

is rajta van. Mivel

F_{0}

C_{2} C_{3}

szakasz felezőpontja, és a

C_{0} C_{1}

C_{2} L_{0}

egyenesek párhuzamosak, az

L_{0}

pont

F_{0}

-ra vonatkozó tükörképe rajta van a

C_{0} C_{1}

egyenesen. Ugyanígy kapjuk, hogy ez a tükörkép rajta van az

A_{0} A_{1}

B_{0} B_{1}

magasságvonalakon is, tehát ez a tükörkép az

M_{0}

magasságpont. Eszerint

F_{0}

valóban felezi az

L_{0} M_{0}

szakaszt.
II. Az

S_{0}

centrumú

(- 1 / 2)

arányú centrális hasonlóság az

A_{0} B_{0} C_{0}

háromszöget az

A_{2} B_{2} C_{2}

háromszögbe viszi, tehát az

A_{0} B_{0} C_{0}

köré írható kört az

A_{2} B_{2} C_{2}

köré írható körbe és az elsőnek

L_{0}

középpontját a másodiknak a középpontjába,

F_{0}

-ba viszi, vagyis

S_{0}

F_{0} L_{0}

szakasz

F_{0}

-hoz közelebbi harmadolópontja. Mivel másrészt

F_{0}

felezi az

L_{0} M_{0}

szakaszt, ezekből következik, hogy

S_{0}

L_{0} M_{0}

szakasz

L_{0}

-hoz közelebbi harmadolópontja.
Rátérünk az előrebocsátott a), b), c) állítások bizonyítására. Jelöljük az eredeti háromszöget

H

-val, a hozzáírt körök középpontjai által meghatározott háromszöget

H_{1}

-gyel,

H

középháromszögét

H_{2}

-vel. Mivel a

H

-hoz írható körök középpontjai rendre a

H

két külső és egy belső szögfelezőjének a metszéspontjai, ezért

H_{1}

oldalai

H

-nak külső szögfelezői, továbbá

H

belső szögfelezői a

H_{1}

-ben magasságvonalak. Eszerint

K^{*}

H_{1}

-nek magasságpontja,

H

H_{1}

-nek talpponti háromszöge, és a

H

köré írható kör

H_{1}

-nek Feuerbach-köre. Tehát az I. állítás szerint

L^{*}

felezi a

K^{*} L

szakaszt, amint azt a)-ban állítottuk. Mivel az

M

S

L^{*}

pont rendre

H

magasságpontja, súlypontja, és köréje írt körének a középpontja, azért a II. állítást

H

-ra alkalmazva kapjuk a b) állítást. Az

S

centrumú,

(- 1 / 2)

arányú hasonlóság

H

-t

H_{2}

-be,

K^{*}

-ot

K

viszi, tehát

S

K K^{*}

szakasz

K

-hoz közelebbi harmadolópontja. Ezzel a c) állítást is bebizonyítottuk, megoldásunk végére értünk.