Kezdőlap


Feladat:	F.1680	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Angyal J. , Balogh Z. , Bognár B. , Chikán B. , Dombi G. , Egyedi Gy. , Engedi A. , Fayekas G. , Füredi Z. , Földes T. , Gál P. , Garay B. , Glódy A. , Golda J. , Győry Gy. , Hadik Róbert , Hangos Katalin , Hermann T. , Hoffer J. , Horváth L. , Horváthy P. , Jakab F. , Kabay Gy. , Kaczkó G. , Karakas L. , Katona E. , Kérchy L. , Kertész Á. , Kuhár J. , Lakatos B. , Major T. , Martoni V. , Nyilánszky M. , Pásztor I. , Pattantyús P. , Pazár B. , Petz D. , Poór Zs. , Pósfai J. , Prácser E. , Prőhle T. , Reviczky J. , Sailer K. , Selényi P. , Simon Júlia , Skopál I. , Szabó András , Szász Gy. , Török I. , Vajnági A.
Füzet:	1970/április, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Derékszögű háromszögek geometriája, Trapézok, Négyszögek középvonalai, Síkgeometriai számítások trigonometria nélkül négyszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Feladat
Hivatkozás(ok):	Feladatok: 1969/október: F.1680

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Három körünk második közös érintőjének létezéséhez elég azt belátnunk, hogy középpontjaik egy $e$ egyenesen vannak. Ez az egyenes ugyanis közös szimmetriatengelyük, tehát az $A B$ közös érintőnek $e$ -re vett tükörképe szintén érinti mindhárom kört.
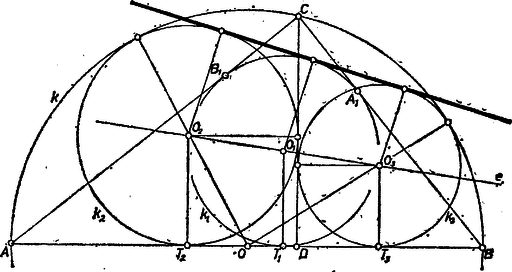
Legyen a $k_{i}$ kör $(i = 1,2,3)$ középpontja $O_{i}$ , sugara $r_{i}$ , $A B$ -n levő érintési pontja $T_{i}$ , a $k$ félkör középpontja $O$ , átmérője $c$ . Azt fogjuk bebizonyítani, hogy $O_{1}$ az $O_{2} O_{3}$ szakasz felezőpontja, vagyis hogy $O_{1} T_{1} = r_{1}$ egyenlő az $O_{2} T_{2} T_{3} O_{3}$ derékszögű trapéz $(O_{2} T_{2} + T_{3} O_{3}) / 2 = (r_{2} + r_{3}) / 2$ középvonalával, és hogy $T_{1}$ felezi a trapéz $T_{2} T_{3}$ magasságát.

Legyen

k_{2}

C D A

derékszögtartományban, ekkor

k_{3}

C D B

-ben van. Feltehetjük, hogy

C B \leq C A

, így

D

O B

szakaszon, esetleg éppen

O

-ban van; legyen

O D = d

. Mivel

k_{2}

érinti a

C D

szakaszt, azért

T_{2} D = r_{2}

, a

k

-val való belső érintkezése alapján pedig

O O_{2} = O A - r_{2} = c / 2 - r_{2}

. Az

O O_{2} T_{2}

derékszögű háromszögben

O T_{2} = | d - r_{2} |

, és így

\begin{matrix} {(d - r_{2})}^{2} + r_{2}^{2} = {(\frac{c}{2} - r_{2})}^{2}, \end{matrix}

\begin{matrix} r_{2}^{2} - (2 d - c) r_{2} - (\frac{c^{2}}{4} - d^{2}) = 0. \end{matrix}

Mivel

d < c / 2

, az

r_{2}

-t nem tartalmazó tag, az egyenlet két gyökének szorzata negatív, azért a gyökök valósak, egyikük pozitív, másikuk negatív. A pozitív gyökre van csak szükségünk:

\begin{matrix} r_{2} = d - \frac{c}{2} + \sqrt[]{c (\frac{c}{2} - d)}, \end{matrix}

és itt a gyökjel alatt

A B (O B - O D) = A B \cdot D B = B C^{2}

áll, hiszen

A B C

derékszögű háromszög, ezért

\begin{matrix} r_{2} = d - \frac{c}{2} + B C = B C - B D . \end{matrix}

(1)

Hasonlóan az

O O_{3} T_{3}

derékszögű háromszögben

O O_{3} = c / 2 - r_{3},

O T_{3} = O D + D T_{3} = d + r_{3},

Pitagorasz tétele alapján

\begin{matrix} r_{3}^{2} + (2 d + c) r_{3} - (\frac{c^{2}}{4} - d^{2}) = 0, \end{matrix}

ennek pozitív gyöke

\begin{matrix} r_{3} = - d - \frac{c}{2} + \sqrt[]{c (\frac{c}{2} + d)} = - A D + A C, \end{matrix}

és így az

O_{2} T_{2} T_{3} O_{3}

trapéz középvonalának hossza

\begin{matrix} \frac{r_{2} + r_{3}}{2} = \frac{B C + A C - A B}{2} . \end{matrix}

(2)

Mármost a jobb oldali kifejezés ‐ mint ismeretes ‐ megadja a

C

-nél derékszögű

A B C

háromszögbe beírt kör sugarát, ami

r_{1}

, eszerint (2) a fenti állítás első részét bizonyítja.

k_{1}

értelmezéséből az is adódik, hogy ‐

B C

-n való érintési pontját

A_{1}

-gyel jelölve ‐ fennáll

B T_{1} = B A_{1} = B C - C A_{1} = B C - r_{1}

.
Így, felhasználva (1)-et, majd (2)-t

\begin{matrix} T_{2} T_{1} = T_{2} B - T_{1} B = (r_{2} + D B) - (B C - r_{1}) = r_{1} = \frac{r_{2} + r_{3}}{2} = \frac{T_{2} D + D T_{3}}{2} = \frac{T_{2} T_{3}}{2}, \end{matrix}

ez pedig állításunk második része.
Ezek szerint

T_{1}

felezi a trapéz

T_{2} T_{3}

szárát, az itt

A B

-re merőlegesen, vagyis az alapokkal párhuzamosan felmért

r_{1} = T_{1} O_{1}

szakasz a trapéz középvonala, tehát

O_{1}

O_{2} O_{3}

száron van. Ezt akartuk bizonyítani.

Hadik Róbert (Makó, József A. Gimn., IV. o. t.)