Feladat: 1579. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1969/február, 55 - 56. oldal  PDF  |  MathML 
Témakör(ök): Számhalmazok, Ponthalmazok, Feladat
Hivatkozás(ok):Feladatok: 1968/január: 1579. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A definíció b) része más szavakkal azt jelenti, hogy a H halmazhoz tartozó minden X, Y pontpárral együtt az XY szakasz X felőli első negyedelő pontja is H-hoz tartozik, és X és Y szerepét megcserélve ugyanúgy adódik, hogy az Y felőli negyedelő pont is H-hoz tartozik.
Elég azt belátni, hogy ha H-nak úgy képezzük pontjait, hogy egy-egy lépésben az előző lépésben létrejött minden szakasznak vesszük az első és harmadik negyedelő pontját, akkor az n-edik lépés után létrejövő szakaszok hossza nem nagyobb, mint AB/2n. Valóban, ha ez így van, és kijelölünk az AB intervallumon egy d hosszúságú PQ szakaszt, akkor csak úgy kell választanunk n-et, hogy AB/2n<d legyen. Így az n-edik lépés után keletkező mindegyik intervallum rövidebb lesz d-nél, tehát egyik sem tartalmazhatja PQ-t, tehát H-nak az első n lépésben létrejött pontjai közül jut PQ belsejébe is.
A kimondott állítás viszont nyilvánvaló, hiszen az első lépésben két AB/4 hosszúságú és egy AB/2 hosszúságú szakasz keletkezik, és minden további lépésben is minden szakaszt a két szélső negyedére és középen egy fele akkora szakaszra vágunk. Így minden lépésben a fellépő legnagyobb szakasz az előző lépés utáni legnagyobb szakasz fele lesz, az n-edik lépés után tehát AB-nek a 2n-ed része.
Ezzel a feladat állitását bebizonyítottuk.

 

Megjegyzés. A leírt eljárást vég nélkül folytatva sem bizonyos, hogy H minden pontját megkapjuk, hiszen nem vesszük minden két H-beli pont közti szakasz negyedelő pontjait, csak az olyanokéit, amelyek végpontjai az eljárás valamelyik lépése után szomszédosak.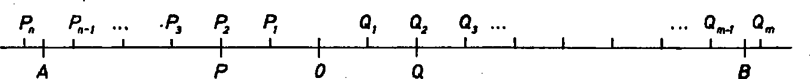
 

 

II. megoldás. Tegyük fel, hogy van olyan az AB szakaszon fekvő PQ szakasz, mely H egyetlen pontját sem tartalmazza. Legyen O a PQ szakasz felezőpontja. Mérjük fel az AB szakasz egyenesén az O pontból mindkét irányban a d=PQ/4 szakaszt annyiszor, amíg az A, B pontokat át nem lépjük. Jelöljük a kapott végpontokat rendre P1, P2, ..., Pn-nel, ill. Q1, Q2, ..., Qm-mel (P=P2, Q=Q2), vagyis n, ill. m az első természetes szám, amelyre nd>OA, ill. md>OB teljesül. Nevezzük az i<n természetes számot jónak, illetve rossznak aszerint, hogy a Pi+1, Pi szakasz tartalmazza-e H valamely pontját, vagy sem. Ekkor az 1 rossz szám, az (n-1) pedig jó szám. Legyen k a legkisebb jó szám. Hasonló módon legyen l az a legkisebb természetes szám, amelyre a QlQl+1 szakasz tartalmazza H valamely pontját.
Így a PkQl szakaszon nincs H-nak pontja, de a Pk+1Pk, és QlQl+1 szakaszon van, legyen ezekben egy-egy a H-hoz tartozó pont X, ill. Y. Ekkor az értelmezés b) része szerint az XY szakasz azon Z pontja is H-hoz tartozik, melyre ZY=3XZ, azaz XZ=XY/4. Az XY szakasz tartalmazza a PkQl szakaszt, ez pedig a PQ szakaszt, tehát XZ=XY/4≥PQ/4=d, és ZY=3XZ≥3d. Emiatt Z a PkQl szakaszon van, ami ellentmond e szakasz megválasztásának.
Feltevésünk tehát nem volt helyes, nem lehet, hogy legyen olyan PQ szakasz, amelyen ne volna H-nak pontja. Ezzel a feladat állítását bebizonyítottuk.
 

Megjegyzés. Volt, aki úgy gondolt indirekt bizonyítást adni, hogy ha PQ-ra nem esnék pontja H-nak, akkor veszi H-nak AP-ben levő, P-hez legközelebbi és QB-ben Q-hoz legközelebbi pontját. Ilyen pontok azonban nem feltétlenül léteznek. Előfordulhat, hogy az A és P közti C, valamint P közt nincs H-nak pontja, C sem tartozik H-ba, de minden nagyobb C'P szakaszban már van pontja H-nak; pl. az A-tól (1-1/4n)AC távolságra eső pontok minden n természetes számra H-hoz tartoznak.