Kezdőlap


Feladat:	1576. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1968/november, 122 - 125. oldal		PDF \| MathML
Témakör(ök):	Poliéderek súlypontja, Térgeometriai bizonyítások, Tetraéderek, Helyvektorok, Feladat
Hivatkozás(ok):	Feladatok: 1967/december: 1576. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A lapok egybevágóságából következik, hogy a tetraéder bármelyik két szemben levő ‐ azaz közös csúccsal nem bíró ‐ éle egyenlő hosszú. Ez nyilvánvaló akkor, ha az $A B C D$ tetraéder egy lapja egyenlő oldalú háromszög. Ha a $B C = a$ , $C A = b$ , $A B = c$ alapélek között van két különböző, pl. $b \neq c$ , akkor a közös oldalú $B C A$ és $B C D$ háromszögek csak úgy lehetnek egybevágók, ha $D B$ vagy $A B$ -vel vagy $A C$ -vel egyenlő (1. ábra).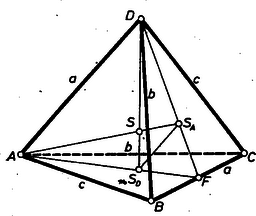

1. ábra

Az első esetből továbbmenve

D C = A C

, így azonban az

A D C

háromszög nem lehet egybevágó az

A D B

háromszöggel, mert mindkettő egyenlő szárú, és a két szárhossz különböző. Ezért

D B = A C

, amint állítottuk.
A tetraéder súlypontján súlyvonalainak metszéspontját értjük, egy súlyvonalán pedig egyik csúcsát a szemben levő lapháromszög súlypontjával összekötő egyenest. Megmutatjuk, hogy a négy súlyvonal valóban egy pontban metszi egymást.
Legyen a

B C A

és

B C D

lapok súlypontja

S_{D}

, ill.

S_{A}

, és közös

B C

élük felezőpontja

F

. Ekkor az

A S_{A}

D S_{D}

súlyvonalak benne vannak az

A D F

síkban, hiszen

S_{A}

D F

(lapbeli) súlyvonalon,

S_{D}

pedig az

A F

súlyvonalon van, éspedig ezeknek

F

-hez közelebbi harmadoló pontja. Ezért az

F S_{D} S_{A}

háromszög 1:3 arányú kicsinyítettje az

F A D

háromszögnek

F

-ből mint középpontból, tehát

A D = 3 \cdot S_{D} S_{A}

S_{D} S_{A} ∥ A D

. Így az

A S_{D} S_{A} D

négyszög trapéz, átlóinak ‐ a tetraéder kiszemelt súlyvonalainak ‐ metszéspontját

S

-sel jelölve

S S_{A} S_{D}

és

S A D

hasonló háromszögek, és

\begin{matrix} S S_{A} : S A = S S_{D} : S D = S_{A} S_{D} : A D = 1 : 3, \end{matrix}

S_{A} S = S_{A} A / 4

S_{D} S = S_{D} D / 4

. Eszerint bármely tetraéder bármelyik két súlyvonala úgy metszi egymást, hogy a metszéspont a súlyvonalnak a laphoz közelebbi negyedelő pontjában van, tehát az

S_{D} D

súlyvonalat a további két súlyvonal is ugyanott metszi. Ezt akartuk bizonyítani.
Esetünkben

A F = D F

, mert egybevágó háromszögek egymásnak megfelelő ‐ ti. a közös

B C

oldalhoz tartozó ‐ súlyvonalai, ezért az imént felhasznált trapéz szimmetrikus, és így

S A = S D

. Ugyanezzel a meggondolással az

A C B

A C D

háromszög-pár egybevágóságából

S B = S D

, és hasonlóan

S C = S D

, így az

S

körül

S D

sugárral írt gömb átmegy a tetraéder mindegyik csúcsán, tehát a feladat állítása igaz.

II. megoldás. Támaszkodunk az

S

súlypontnak az I. megoldásban bebizonyított tulajdonságaira.
Fordítsuk bele a

D

-ben összefutó

D B C

D C A

D A B

oldallapot rendre a

B C

C A

A B

alapél körül az

A B C

alaplap síkjába, éspedig úgy, hogy egyik se fedje az alaplapot; legyen

D

új helyzete rendre

D_{a}

D_{b}

D_{c}

(2. ábra).

2. ábra

Ekkor a

D_{b} D_{c}

egyenes átmegy

A

-n, mert az

A D_{b}

A D_{c}

félegyenesek közti szög egyenlő az

A B C

háromszög szögeinek összegével. Egyszersmind

A

felezi a

D_{b} D_{c}

szakaszt, így az

A B C = H_{1}

háromszög a

D_{a} D_{b} D_{c} = H_{2}

háromszög középháromszöge, így

S_{D}

súlypontjuk közös, és

H_{2}

H_{1}

-ből úgy is előáll, ha azt az

S_{D}

pontra tükrözzük, majd a képét ugyancsak

S_{D}

-ből mint középpontból a kétszeresére nagyítjuk.
Az oldallapokat alapélük körül forgatva a

B C D

háromszög

D

csúcsa a

D_{a}

-ból

B C

-re bocsátott merőlegesnek

D_{a} D'_{a}

szakasza fölött halad, ahol

D'_{a}

D_{a}

pontnak a

D_{b} D_{c}

egyenesen levő vetülete. Ez

H_{2}

-nek magasságvonala, hiszen

D_{b} D_{c} ∥ B C

. Ugyanígy a visszaforgatás folyamán a

D_{b} D'_{b}

, ill.

D_{c} D'_{c}

magasságszakasz fölött halad

D

, tehát csak e szakaszok közös pontja fölött lehet, és csak akkor jön létre, ha a magasságszakaszoknak van közös pontja, vagyis ha az

A B C

háromszög hegyesszögű. A közös pont a háromszög

M

magasságpontja. Hegyesszögű háromszögből kiindulva viszont

D

mindig létrejön.
Ebből kapjuk, hogy a tetraéder

S

súlypontjának a

H_{1}

síkján levő

S'

vetülete negyedeli az

S_{D} D' = S_{D} M

szakaszt, ennélfogva azt kell belátnunk, hogy

S'

H_{1}

köré írt kör középpontja, hiszen

S

csak így lehet egyenlő távolságra

H_{1}

csúcsaitól. Ehhez elég belátnunk, hogy

S'

a fenti két transzformáció útján áll elő a

H_{2}

köré írt kör

O

középpontjából. Valóban,

O

S_{D}

és

M

H_{2}

-nek Euler-féle egyenesén a mondott sorrendben úgy feküsznek, hogy

O S_{D} = S_{D} M / 2

, ezért a fentiek szerint

S'

is az egyenesen van, az

O S_{D}

szakasz

S_{D}

-n túli meghosszabbításán, és

S_{D} S' = S_{D} M / 4 = S_{D} O / 2

. Ezt akartuk bizonyítani, ebből

S A = S B = S C

.
Meggondolásunkat a tetraéder egy másik lapján megismételve adódik, hogy

D

-nek

S

-től való távolsága egyenlő az előbbi 3 távolsággal. Evvel az állítást bebizonyítottuk.

III. megoldás. A súlypont negyedelő tulajdonsága folytán elég belátnunk, hogy a tetraéder súlyvonalai egyenlő hosszúak. Ez az 1121. gyakorlatban¹ bebizonyított tételből adódik, ugyanis esetünkben

\begin{matrix} D S_{D}^{2} = \frac{1}{3} (D A^{2} + D B^{2} + D C^{2}) - \frac{1}{9} (A B^{2} + B C^{2} + C A^{2}) = \frac{2}{9} (a^{2} + b^{2} + c^{2}), \end{matrix}

és ugyanez adódik mindegyik súlyvonalra.

IV. megoldás. Legyenek a tetraéder csúcsainak helyvektorai

a, b, c, d,

ekkor ‐ mint ismeretes ‐ a tetraéder

S

súlypontjának helyvektora

\begin{matrix} s = \frac{1}{4} (a + b + c + d) = \frac{1}{2} [\frac{a + b}{2} + \frac{c + d}{2}] . \end{matrix}

Az utóbbi alakból kiolvasható, hogy

S

A B

szakasz

F_{1,2}

és a

C D

szakasz

F_{3,4}

felezőpontjai közti szakasznak is a felezőpontja. Eszerint bármely tetraéder súlypontja felezi a szemközti él-párjainak felezőpontjai közti szakaszokat.
Tükrözzük a

T = A B C D

tetraédert

S

-re, kapjuk a

T^{*} = A^{*} B^{*} C^{*} D^{*}

tetraédert. A fentiek alapján az

A^{*} B^{*}

szakasz felezőpontja azonos a

C D

szakasz felezőpontjával, tehát

A^{*} C B^{*} D

paralelogramma. Hasonlóan paralelogramma az

A^{*} B C^{*} D

A^{*} B D^{*} C

négyszög is, és ezek

S

-re vonatkozó

A B^{*} C D^{*}

A B^{*} D C^{*}

tükörképe is, valamint az

A C^{*} B D^{*}

négyszög. A felsorolt

6

lap egy

P

paralelepipedont határol, melynek

S

a középpontja (3. ábra).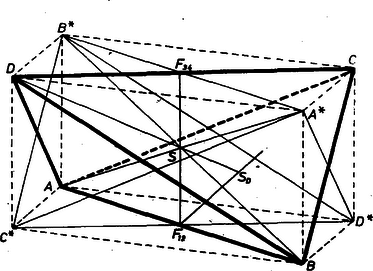

3. ábra

A feladat feltevése szerint

T

szemközti élei egyenlők, ezért

P

lapjain az átlók páronként egyenlők,

P

lapjai tehát téglalapok és

P

téglatest. Ámde a téglatest testátlói egyenlők, tehát

S

P

-nek mindegyik csúcsától, így

T

csúcsaitól is egyenlő távol van. Ezt kellett bizonyítanunk.

Megjegyzés. Megoldásunk alapján bármely

T

téglatestből származtatható egy a feltételeknek megfelelő tetraéder, ennek csúcsai:

T

-nek egy

A

csúcsa és a benne összefutó

3

lapnak

A

-val szemben levő csúcsa. ‐ Ha

T

élei

a

b

c

, különbözők, akkor a tetraéder szemben fekvő élpárjai

\begin{matrix} \sqrt[]{a^{2} + b^{2}}, \sqrt[]{b^{2} + c^{2}}, \sqrt[]{c^{2} + a^{2}}, \end{matrix}

szintén különbözők, és a belőlük alkotott háromszög hegyesszögű, mert pl. az első kettő közti

ε

szögre

\begin{matrix} cos ε = b^{2} / \sqrt[]{(a^{2} + b^{2}) (b^{2} + c^{2})} > 0. \end{matrix}

V. megoldás. A 2. ábrán a tetraéder lapjaira belülről tekintünk rá. Ebből azt is látjuk, hogy a

4

lap megfelelő csúcsait ugyanabban a sorrendben körüljárva ugyanolyan forgási irányban járjuk körül a lapokat. Eszerint ugyanez áll akkor is, ha a lapokra kívülről nézünk. Így pedig a tetraédert bármelyik lapjánál fogva az eredeti helyére állíthatjuk, az illető lap csúcsait az alap megfelelő csúcsaihoz illesztve, és ekkor a

4

. csúcs helyét az alap csúcsaitól mért

3

távolság egyértelműen meghatározza, tehát a

4

. csúcs is illeszkedik az eredeti tetraéder alapjával szemközti csúcsához. Ebből ismét adódik, hogy a

4

súlyvonal egyenlő.

Megjegyzés. A mondottakból az is következik, hogy a szóban forgó tulajdonságú tetraéderek súlypontja a

4

laptól is egyenlő távolságra van, tehát a súlypont egyszersmind a beírt gömbnek is középpontja. Ezek szerint van olyan, nem szabályos háromszöglapokkal határolt tetraéder, melyben a látott

3

nevezetes pont egybeesik. (A síkban viszont a súlypont, a körülírt, valamint a beírt kör középpontjai közül bármelyik kettőnek az egybeeséséből következik, hogy a háromszög szabályos.)

¹Lásd a megoldást K. M. L. 35 (1967) 216. o.