| Feladat: | 1375. matematika feladat | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Bárány I. , Bede Mária , Cser László , Cserháti Zsuzsa , Cziffra A. , Dabóczi Á. , Deák J. , Domokos L. , Ferenczi Gy. , Herényi I. , Kiss A. , Kovács Kristóf , Lévai F. , Nagy Zsuzsa , Scsaurszky P. , Sükösd Cs. , Szalay M. , Szántó O. , Szeidl L. , Szörényi M. , Tényi G. , Tongori Éva , Vesztergombi Katalin | ||
| Füzet: | 1965/november, 150 - 152. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Csillagászati, földrajzi feladatok, Gömbi geometria, Numerikus módszerek, Koszinusztétel alkalmazása, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1965/február: 1375. matematika feladat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.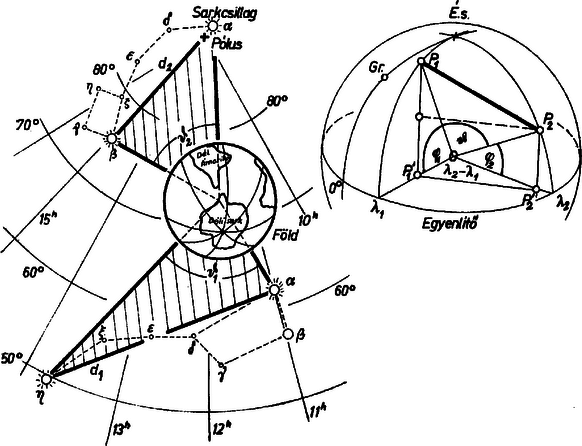 A Föld és a két csillag ( és ) által meghatározott háromszögben ismerjük az és oldalakat, továbbá az adott koordinátákból kiszámíthatjuk a köztük levő szög koszinuszát az idézett
így (1) tagjait logaritmussal számítva az első pár esetében a második pár esetében ennélfogva a két távolságra a koszinusz-tételt alkalmazva Így a két legtávolabb látszó csillag távolsága a Göncöl Szekér esetében Megjegyzés. Az (1) képletet egymás után az 1295., az 1214., az 1146. és az 1045.2 feladatra való hivatkozással használtuk fel, erre tekintettel közöljük egy az idézett legkorábbi helyen találhatótól különböző bizonyítását. Legyen a Cser László (Csorna, Hunyadi J. g. III. o. t.) 2K. M. L. 22 (1961) 157. o. |