Kezdőlap


Feladat:	1374. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babai László , Balogh K. , Bárány I. , Deák J. , Domokos L. , Elekes Gy. , Ferenczi Gy. , Fodor Magdolna , Herényi I. , Herszényi B. , Hoffmann Gy. , Höss Rozália , Joó Piroska , Juhász F. , Karsai Kornélia , Kemény Cs. , Kiss Á. , Korchmáros G. , Krigler F. , Kövesdi Gy. , Lévai F. , Majtényi G. , Márki L. , Molnár Ágnes , Nagy Klára , Óhegyi E. , Palotás Á. , Racskó P. , Sarkadi-Nagy I. , Scsaurszky P. , Simig Gy. , Surányi L. , Sükösd Cs. , Székely G. , Szemkeő Judit , Szörényi M. , Takács J. , Tényi G. , Vadász I. , Vermes D. , Vesztergombi Katalin
Füzet:	1965/október, 76 - 77. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Trigonometriai azonosságok, Háromszögek nevezetes tételei, Háromszög nevezetes körei, Szinusztétel alkalmazása, Síkidomok súlypontja, Feladat
Hivatkozás(ok):	Feladatok: 1965/február: 1374. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A színusz-tétel szerint a háromszög két szöge színuszának aránya egyenlő a szemben fekvő oldalak arányával; mondhatjuk tehát, hogy az $A B C$ háromszög egymás utáni csúcsaiba helyezett $m_{A}$ , $m_{B}$ , $m_{C}$ tömeg arányos rendre a $B C$ , $C A$ , $A B$ oldal hosszával.
Így a $B$ és $C$ csúcsokba helyezett tömeg-pár $M$ súlypontja¹ a $B C$ szakasznak az a pontja, amelyre

\begin{matrix} M B : M C = m_{C} : m_{B} = A B : A C . \end{matrix}

Ismeretes, hogy ugyanebben a pontban metszi a

B C

oldalt a

B A C

szög (belső) felezőegyenese, eszerint

A M

a szögfelező.
A három tömegpontból álló rendszer súlypontja az idézett tétel szerint az

A M

szakaszon, vagyis az

A

-ból induló szögfelezőn van.
Az első két pont más megválasztásából hasonlóan adódik, hogy a keresett súlypont mindegyik szögfelezőn rajta van, ezért azonos a háromszögbe írt kör középpontjával.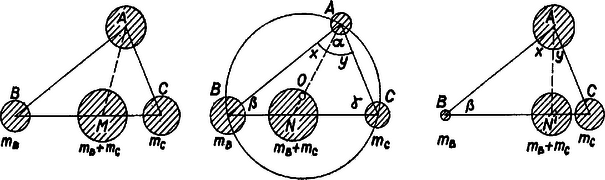

II. A második esetben legyen a

B

C

tömeg-pár súlypontja

N

, és fejezzük ki a

B N

C N

szakaszokat a

B N A

C N A

háromszögből a

B A N = x

, ill.

C A N = y

szögek felhasználásával, a színusz-tétel alapján.

\begin{matrix} B N : C N = & \underset{̲}{\frac{A N sin x}{sin β} : \frac{A N sin y}{sin γ}} = m_{C} : m_{B} = & (1) \\ = sin 2 γ : sin 2 β = \underset{̲}{2 sin γ cos γ : 2 sin β cos β .} \end{matrix}

Hegyesszög kétszeresének színusza pozitív, ezért

N

B C

szakasz belső pontja, tehát

x + y = α

, és így az aránypár aláhúzott részeiből az addíció tételek alkalmazásával

\begin{matrix} \frac{sin x}{sin y} = \frac{sin (α - y)}{sin y} = sin α ctg y - cos α = \frac{cos γ}{cos β}, & (2) \\ ctg y & = \frac{cos γ + cos α cos β}{sin α cos β} = \frac{- cos (α + β) + cos α cos β}{sin α cos β} = \\ = \frac{sin α sin β}{sin α cos β} = tg β . \end{matrix}

Eszerint a

C N

szakasszal szemközti szög

y = C A N ∢ = 90^{\circ} - β

. Ugyanekkora a

C A O

szög is, ahol

O

a háromszög körülírt körének középpontja, hiszen az

A C O

egyenlő szárú háromszög

O

-nál levő szöge

2 β

.
Így az I. esethez hasonlóan kapjuk, hogy a tömegpontrendszer súlypontja a háromszög köré írt kör középpontja.
III. A tangensekkel arányos tömegek esetében az előbbi számítás annyiban módosul, hogy (1) utolsó arányában

cos γ

és

cos β

szorzó helyett osztó lesz, (2) jobb oldalára a reciproka kerül,

β

és

γ

felcserélődik, így

ctg y = tg γ

adódik. Eszerint

y

γ

pótszöge, a

B

-be és

C

-be helyezett tömeg-pár súlypontját az

A

-ból húzott magasság metszi ki, és a keresett súlypont ‐ az első eset záró meggondolásához hasonlóan ‐ a háromszög magassági pontja.

Megjegyzés. Az I. részben nem használtuk ki, hogy a háromszög hegyesszögű, az az eredmény minden háromszögre érvényes. Érvényes a II. rész eredménye is, valamint a III-é is a derékszögű háromszög kivételével, ezekben az esetekben a tompaszög csúcsában elhelyezett tömeget negatívnak gondoljuk, ill. oda fölfelé ható erőt gondolunk (alkalmasan elhelyezett csigán át hat a tömeg súlya).
Babai László (Budapest, Fazekas M. gyak. g. I. o. t.)

¹Lásd pl. az 1246. feladat I. megoldását, K. M. L. 29 (1964) 117. o.