Feladat:	1335. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Arányi P. ,  Bárány I. ,  Deák J. ,  Demetrovics J. ,  Dévaj Ágnes ,  Domokos L. ,  Füvesi I. ,  Huhn A. ,  Kajcsos Zs. ,  Kálmán A. ,  Kövér Á. ,  Lévai F. ,  Molnár Ágnes ,  Petrovich I. ,  Racskó P. ,  Recski A. ,  Rimóczy P. ,  Szörényi Miklós ,  Tényi G. ,  Vajda A.
Füzet:	1965/szeptember, 21 - 22. oldal		PDF  |  MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Kör egyenlete, Négyzetrács geometriája, Síkbeli szimmetrikus alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1964/szeptember: 1335. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.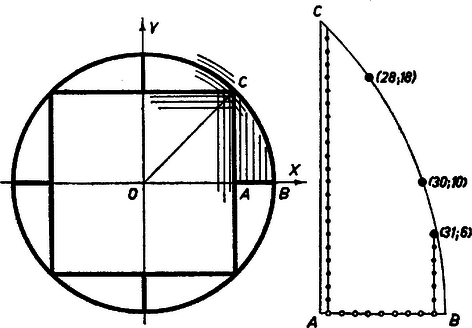   a) A körbe négyzetet írunk, melynek az oldalai párhuzamosak a tengelyekkel, az így levágott körszeleteket megfelezzük a tengelyek beléjük eső szakaszaival, és a rácspontokat az így felosztott kör részeiben és az osztásvonalakon számláljuk meg, felhasználva egyszerűsítéshez a szimmetriákat. A négyzet oldalai az $x=\pm \sqrt[]{500}$, $y=\pm \sqrt[]{500}$ egyenesek, ezeken nincs rácspont, mert $500$ nem négyzetszám. $\sqrt[]{500}\approx 22\mathrm{,}3\text{...}$, eszerint a négyzet belsejében vannak mindazok a rácspontok, amelyek mindkét koordinátájának abszolút értéke nem nagyobb $22$-nél, számuk ${\left(2\cdot 22+1\right)}^2=2025$. A körszeleteket kettévágó szakaszokon ugyanannyi rácspont van. Az $X$-tengely pozitív felén levő $AB$ szakasz első rácspontjának abszcisszája az előzők szerint $23$, az utolsóé $31$, mert $B$ abszcisszája $r=31\mathrm{,}6\text{...}$, így a rácspontok száma a szakaszon $31$‐$22$, a $4$ ilyen szakaszon pedig $36$. Már csak az $ABC$ fél körszelet belsejében és a $BC$ íven levő rácspontok megszámlálása van hátra, mert a kör még nem tekintett $7$ része ebből az origó körüli ${90}^{\circ }$-os forgatásokkal, a tengelyeken és a tengelyek $OC$ felezőjén való tükrözésekkel előállítható, és minden ilyen szimmetria a rácspontokat is egymásba viszi át. Az $ABC$ idom mondott rácspontjait a rajtuk átmenő, az $Y$-tengellyel párhuzamos $x=23$, $24$, $\text{...}$, $31$ egyenesek szerint csoportosítva számláljuk meg. Ehhez táblázatban feltüntetjük a $BC$ íven levő metszéspontjuk $y=\sqrt[]{1000-x^2}$ ordinátáját, így rácspontjaik $n$ száma mindig $y$ egész része. Az $n$ oszlopban álló számok összege $136$, így a körben levő rácspontok száma $\begin{array}{c}{\displaystyle 2025+36+8\cdot 136=3149.}\end{array}$ b) Az eddigieket a további előírt $r^2$ értékek esetéhez is felhasználhatjuk. Az ezekhez tartozó négyzetekben, az $AB$ szakaszon és szimmetrikusain a rácspontok száma annyi, mint $r^2=1000$ esetén, mert ehhez képest a legkisebb és a legnagyobb $r^2$ érték esetében a négyzetgyökök egész része változatlan: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \sqrt[]{497\mathrm{,}5}=22\mathrm{,}3\text{...}\mathrm{,}\sqrt[]{995}=31\mathrm{,}5\text{...}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \sqrt[]{502\mathrm{,}5}=22\mathrm{,}4\text{...}\mathrm{,}\sqrt[]{1005}=31\mathrm{,}7\text{...}\mathrm{.}}\hfill \end{array}}$ A táblázat szerint a $\left(26;18\right)$ és a $\left(30;10\right)$ rácspont rajta van a $BC$ íven. Ezért a kisebb $r^2$ értékekre áttérve az $ABC$ idomban $2$-vel, a körben pedig $8\cdot 2=16$-tal csökken a rácspontok száma. Hasonló eset adódhat, ha az $y^2$ oszlopban álló számot egymás után $1$-gyel, $2$-vel, $\text{...}$, $5$-tel csökkentve négyzetszámot kapunk. Egyetlen ilyen eset az $x=31$ egyenes esete, amelyben $997-{31}^2=6^2$, eszerint $r^2$-et $996$-ra csökkentve a kör rácspontjainak száma ismét $8$-cal csökken. $r^2$-et $1005$-ig növelve a körív nem megy át újabb rácspontokon, mert az $y^2$ oszlop számait $1$-gyel, $2$-vel, $\text{...}$, $5$-tel növelve sehol sem lépünk négyzetszámra. Ezek szerint $r^2$ összes vizsgált értékeihez a megfelelő kör belsejében és kerületén levő rácspontok együttes $N$ száma, valamint közülük a kerületen levők $M$ száma ${\displaystyle \begin{array}{ccccccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>r</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mphantom><mn>1</mn></mphantom><mn>995</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>996</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>997</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>998</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>999</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1000</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1001</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1002</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1003</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1004</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1005</mn></math>,}}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>N</mi><mo stretchy="false">=</mo><mn>3125</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3125</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3133</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3133</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3133</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3149</mn></math>,}}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>M</mi><mo stretchy="false">=</mo><mphantom><mn>325</mn></mphantom><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>8</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>16</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>,}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>. }}\end{array}}$ Szörényi Miklós (Pécs, Széchenyi I. g. IV. o. t.)   Megjegyzések. I. Hasonló, de kissé hosszabb számítás szerint az $r^2=1000$ értéket megtartva, de a kört a $\left(0\mathrm{,}5;0\right)$, vagy a $\left(0\mathrm{,}5;0\mathrm{,}5\right)$ pont körül írva a rácspontok száma mindkét esetben $3144$. 2. Kézenfekvő sejtés, (amit a ,,közelítőleg'' megfelelő precizírozása mellett nem túl nehéz igazolni), hogy a koordinátarendszerbe egy elég nagy konvex idomot helyezve a benne levő rácspontok száma és az idom területének mértékszáma közelítőleg egyenlők. Erre támaszkodva eredményeinkből $\pi$-re kaphatunk $3\mathrm{,}14$ körüli közelítő értéket.