Kezdőlap


Feladat:	1314. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bóta K. , Deák I. , Dobozy O. , Horányi S. , Hortobágyi J. , Huhn A. , Kafka P. , Kerényi I. , Körner J. , Lux I. , Márki László , Mátrai M. , Nagy Klára , Pelikán J. , Sükösd Cs. , Székely G. , Veres F. , Vesztergombi Katalin
Füzet:	1965/április, 162 - 163. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek egybevágósága, Függvényvizsgálat, Terület, felszín, Téglalapok, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1964/április: 1314. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyenek a téglalap oldalai $a$ és $b$ , ahol $a ≧ b (> 0)$ , az oldalakra felmért szakasz hossza $x$ , így a keletkezett négyszögek területét mint $x$ függvényét a

\begin{matrix} 0 < x ≦ b \end{matrix}

(1)

intervallumban kell vizsgálnunk. A felmért szakaszok végpontjait az oldalak sorrendjében összekötve, a téglalapról derékszögű háromszögeket vágunk le, közülük mindkét mód esetében

2 - 2

egybevágó (az ábra

α

, ill.

β

része). A területek

x

-nek másodfokú függvényei, mindjárt teljes négyzetté kiegészítéssel

\begin{matrix} t_{1} = a b - x (b - x) - (a - x) x = 2 x^{2} - (a + b) x + a b = \\ = 2 {(x - \frac{a + b}{4})}^{2} + a b - {(\frac{a + b}{4})}^{2}, \\ t_{2} = a b - (a - x) (b - x) - x^{2} = - 2 x^{2} + (a + b) x = \\ = - 2 {(x - \frac{a + b}{4})}^{2} + {(\frac{a + b}{4})}^{2} . \end{matrix}

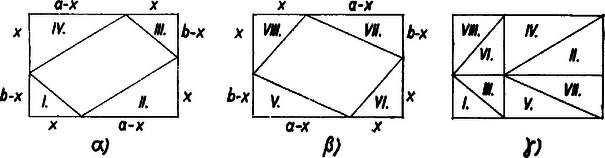Vegyük észre mindjárt, hogy

t_{1} + t_{2} = a b

, azaz a két idom területének összege egyenlő az adott téglalap területével, egyikük növekedésével a másik csökken, így a két kérdésre a választ egy csapásra adhatjuk meg. (Másrészt a lemez feldarabolási tervét mindkét módon elkészítve a levágott

8

háromszög együttes területe is

a b

, ezt mutatja be átdarabolással az ábra

γ

része.)

t_{1}

-nek az

x

-től függő tagja nem negatív, így legkisebb értékét akkor veszi fel, ha ez a tag

0

, vagyis

\begin{matrix} x_{0} = \frac{a + b}{4} esetén t_{1 {min}_{}^{}} = a b - {(\frac{a + b}{4})}^{2}, \end{matrix}

amennyiben

x_{0}

a mondott intervallumba esik, vagyis ha

\begin{matrix} \frac{a + b}{4} ≦ b, b ≧ \frac{a}{3}, \end{matrix}

(2)

egyelőre ezt az esetet tekintjük. A fentiek szerint ugyanezen feltételek mellett

\begin{matrix} t_{2 {max}_{}^{}} = {(\frac{a + b}{4})}^{2} . \end{matrix}

(

t_{1}

-től függetlenül is látható, hogy így

t_{2}

változó tagja

0

, különben pedig negatív.) Ha

a = b

, akkor

x_{0} = a / 2

x

-et

x_{0}

-tól akár lefelé, akár fölfelé távolítva

t_{1}

növekszik, és legnagyobb értékét ott veszi fel, ahol az

| x - x_{0} |

eltérés a legnagyobb. Lefelé nagyobb távolságra távolodhatunk

x_{0}

-tól, mint fölfelé, ugyanis az

x_{0}

-lal kettévágott (1) intervallum első és második része hosszainak különbsége

\begin{matrix} (x_{0} - 0) - (b - x_{0}) = 2 x_{0} - b = \frac{a - b}{2} ≧ 0. \end{matrix}

Eszerint

t_{1}

legnagyobb (és

t_{2}

legkisebb) értéke

x = 0

-nál adódnék:

t_{1} = a b

, ill.

t_{2} = 0

(

t_{2}

elfajul az átlószakasszá), az

x = 0

értéket viszont (1)-ben kizártuk. Eszerint a (2) esetben

t_{1}

nem vesz fel legnagyobb és

t_{2}

nem vesz fel legkisebb értéket.

b < a / 3

a > 3 b

esetén a

t_{1}

-et minden

x

-re ábrázoló parabola alul elhelyezkedő csúcsának (és a

t_{2}

-t ábrázoló parabola fönt elhelyezkedő csúcsának közös)

x_{0}

abszcisszája jobbra esik az (1) intervallumtól, mert

\begin{matrix} x_{0} = \frac{a + b}{4} > \frac{3 b + b}{4} = b . \end{matrix}

Ezért

t_{1}

-et (1)-ben a parabola süllyedő ágának egy íve ábrázolja, így

t_{1}

az (1) jobb végpontjában veszi fel legkisebb értékét:

\begin{matrix} x = b esetén t'_{1 {min}_{}^{}} = b^{2}, és t'_{2 {max}_{}^{}} = a b - b^{2}, \end{matrix}

másrészt

t_{1}

ugyanúgy nem vesz fel legnagyobb értéket és

t_{2}

sem vesz fel legkisebbet, mint az előbbi esetben.
II. A

t_{1} = t_{2}

követelmény a fentiek szerint akkor teljesül, ha

\begin{matrix} 4 x^{2} - 2 (a + b) x + a b = 0, vagyis  ha x_{1} = a / 2, x_{2} = b / 2. \end{matrix}

Az utóbbi érték mindig felmérhető a lemezre, az előbbi csak

a / 2 ≦ b

, azaz

b ≦ a ≦ 2 b

esetén. Mindkét esetben a két mód szerinti felmérés nemcsak egyenlő területű, hanem egyszersmind egybevágó négyszögekre vezet.
Márki László (Budapest, Fazekas M. gyak. g. III. o. t.)