Kezdőlap


Feladat:	903. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágh A. , Arató P. , Bartha L. , Bollobás B. , Füle K. , Gaál S. , Galambos J. , Grallert Ferenc , Győry K. , Hadik Z. , Halász G. , Kisvölcsey J. , Kolonits F. , Kristóf L. , Makay A. , Mihályffy L. , Montvay István , Náray Miklós , Pál G. , Papp Éva , Pődör B. , S. Nagy Erzsébet , Sánta J. , Sárközy A. , Simon L. , Simonfai L. , Szász D. , Szatmáry G. , Tusnády G. , Várallyay L.
Füzet:	1959/január, 23 - 24. oldal		PDF \| MathML
Témakör(ök):	Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1958/április: 903. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Feladatunk állítása úgy is kimondható, hogy az $O$ pontnak $S$ -re vonatkozó $T$ tükörképe rajta van annak a hat síknak mindegyikén, amelyek egy‐egy él felezőpontján áthaladva a szembenfekvő élre merőlegesen állnak. Az állítást ebben az alakban fogjuk bizonyítani, így ugyanis nincs szükség arra, hogy külön vizsgáljuk azt az esetet, amikor $O$ és $S$ egybeesnek, és így az $O S$ egyenes nincs egyértelműen meghatározva.
Jelöljük az $A B C D$ tetraéder tetszés szerint választott $B C$ , $A D$ szembenfekvő éleinek felezőpontjait $F_{1}$ , ill. $F_{2}$ -vel és az ezeken át $A D$ -re merőlegesen állított síkokat $σ_{1}$ , ill. $σ_{2}$ -vel. Minthogy szerkesztésüknél fogva $σ_{1}$ és $σ_{2}$ párhuzamosak, továbbá $S$ felezi a végpontjaival $σ_{1}$ , ill. $σ_{2}$ -re támaszkodó $F_{1} F_{2}$ szakaszt, azért $σ_{1}$ tükörképe $σ_{2}$ -nek $S$ -re vonatkozóan. Ámde $O$ rajta van $σ_{2}$ -n, ennélfogva $S$ -re vonatkozó $T$ tükörképe rajta van $σ_{1}$ -en, amit bizonyítani akartunk. Mindez akkor is érvényes, ha $σ_{1}$ és $σ_{2}$ egybeesnek. Meggondolásunk bármely szemköztes élpárra alkalmazható, mert a $B C$ , $A D$ élpárnak semmi olyan tulajdonságát nem használtuk ki, ami ne volna meg bármely szemköztes élpárnak (nincs is ilyen a feltevésben, hiszen tetszőleges tetraéderről szól az állítás). Ezzel bizonyításunkat befejeztük.

Grallert Ferenc (Miskolc, Földes F. g. III. o. t.)

II. megoldás: Az

O

és

T

, valamint a fenti

F_{1}

F_{2}

pontok paralelogrammát határoznak meg, mert az

O F_{2} T F_{1}

négyszög

O T

és

F_{1} F_{2}

átlóinak közös a felezőpontja:

S

, tehát

T F_{1} ∥ O F_{2}

. Ámde

O

definíciója folytán

O F_{2}

merőleges

A D

-re, így

T F_{1}

is merőleges

A D

-re, tehát

T

benne van az

F_{1}

-en át

A D

-re merőlegesen állított síkban.

Náray Miklós (Bp. VIII., Széchenyi I. g. III. o. t.)

III. megoldás: Az

O

és

T

tükrösségére gondolva tekintsük az egész

A B C D

tetraédernek az

S

súlypontra vonatkozó

A' B' C' D'

tükörképét. Minthogy

S

közös felezőpontja a három szemközti élpár felezőpontjait összekötő szakasznak, azért

A' B' C' D'

élfelező pontjai egybeesnek

A B C D

-éivel pl. (az előző megoldások jelöléseivel)

A' D'

-nek

F'_{2}

felezőpontja egybeesik

B C

-nek

F_{1}

felezőpontjával. És mivel még

A' D'

párhuzamos

A D

-vel, azért az

F_{1}

en át

A D

-re merőlegesen álló sík egybeesik az

F'_{2}

-n át

A' D'

-re merőlegesen álló síkkal, azaz

A' D'

felezőmerőleges síkjával, tehát átmegy

A' B' C' D'

körülírt gömbjének

O'

középpontján, ami pedig a tükrözés folytán éppen

O

-nak

S

-re vonatkozó tükörképe. Evvel az állítást bebizonyítottuk.

Montvay István (Bp. XIX. Landler J. g. IV. o. t.)

Megjegyzés. Jelöljük a

D

csúcsból kifutó

D A

D B

D C

élek felezőpontjait

F_{2}

F_{3}

F_{4}

-gyel. Az

F_{2} F_{3} F_{4}

háromszög a

D

középpontra nézve hasonló helyzetű az

A B C

háromszöggel, ennélfogva az

F_{2}

F_{3}

F_{4}

-en át a

B C

C A

, ill.

A B

élre merőlegesen álló síkok egyben

F_{3} F_{4}

F_{4} F_{2}

, ill.

F_{2} F_{3}

-ra is merőlegesek, így az

F_{2} F_{3} F_{4}

síkot az

F_{2} F_{3} F_{4}

háromszög magasságvonalaiban metszik, egymást pedig abban a

t_{D}

egyenesben, amely átmegy az

F_{2} F_{3} F_{4}

háromszög

M_{1}

magasságpontján és merőleges az

A B C

sí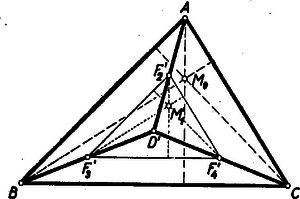kra.

(Az ábra a tetraédernek az

A B C

síkon való merőleges vetületét mutatja, erre utalnak a síkon kívüli pontok jelei mellett álló vesszők.) Eszerint

T

t_{D}

-n van. Az

F_{2} F_{3} F_{4}

háromszöget a tetraéder egyik (a

D

csúcshoz tartozó) középmetszetének nevezve és a középmetszetet mindegyik csúcshoz elkészítve a bebizonyított állítás egy része így is kimondható: a tetraéder középmetszeteinek magasságpontjain át az illető középmetszetek síkjára állított merőlegesek egy ponton mennek át.
Ha

A B C D

ortocentrikus, akkor

F_{2} F_{3} F_{4} D

is ortocentrikus, ezért

D

-ből kiinduló közös magasságvonaluk átmegy az

F_{2} F_{3} F_{4}

, ill.

A B C

lap

M_{1}

, ill.

M_{0}

magasságpontján, azaz

t_{D}

átmegy az

M_{0}

ponton. Eszerint

T

-nek az

A B C D

tetraéder mindnégy lapján való vetülete az illető lap magasságpontja, tehát

T

maga azonos a tetraéder magasságpontjával.