| Feladat: | 821. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Bergmann Gy. , Borsi L. , Elbert Á. , Fekete L. , Frivaldszky S. , Galambos J. , Gárdonyi Z. , Gáspár J. , Gáti Z. , Gergely E. , Glattfelder Gy. , Gyene A. , Győry K. , Horváth M. , Károlyi Gy. , Kolonits F. , Leipniker P. , Makay A. , Megyesi L. , Móricz F. , Papp K. , Papp Z. , Parlagh Gy. , Pásztor Erzsébet , Puruczky Éva , Pödör B. , Répássy Cs. , Rockenbauer A. , Sárközy A. , Schipp F. , Schultz Gy. , Simon L. , Solt Gy. , Stahl J. , Stark G. , Szatmáry Z. , Szekér A. , Tatár I. , Tóth Zsuzsanna , Váczy P. , Vannay L. , Várallyay L. , Veress P. , Veszely Gy. , Wollner R. , Zaránd Péter | ||
| Füzet: | 1957/december, 149 - 151. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Számtani-mértani egyenlőtlenségek, Síkgeometriai számítások trigonometriával, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1957/március: 821. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Három esetet különböztetünk meg: a) A betűzést az 1. ábra mutatja. 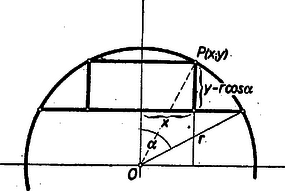 A körszeletbe írt téglalap területe ami független -tól, ha
A mértani közép tételéből a négy tényezős szorzat akkor a legnagyobb, ha a tényezők egyenlőek, vagyis
A maximális területű téglalap területe pedig Mivel (3)-ból b) Ha , akkor vannak a körszeletbe beírt olyan téglalapok, amelyeknek mind a négy csúcspontjuk a körszelet körívén van (pl. a 2. ábrában a szaggatott vonallal kihúzott téglalap). Ilyen téglalap területe 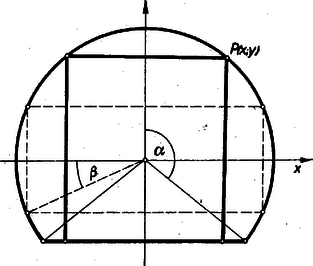
T' tehát maximális, ha , vagyis a maximális területű téglalapot azok közül a téglalapok közül kell keresnünk, amelyeknek egyik oldala a húrra esik. Ez esetben követhető az a)-ban alkalmazott eljárás. Ugyanazokhoz az eredményekhez jutunk, de természetesen mindenütt negatív lesz. c) Ha , akkor a körszelet tartalmaz a körbe írható négyzetet, amely mint ismeretes ‐ és (4)-ből is leolvasható ‐ a körbe írható legnagyobb területű téglalap. Ez esetben általában végtelen sok négyzet rajzolható a körszeletbe, kivéve az határesetet, amikor a húrra mint oldalra rajzolt négyzet az egyetlen megoldás.
|