| Feladat: | 768. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Klopfer Sándor , Kuna János , Pogány Eörs | ||
| Füzet: | 1957/január, 12 - 13. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Eltolás, Egyenesek egyenlete, Trapézok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1956/szeptember: 768. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Jelöljük a trapéz csúcspontjait , , , -vel, az oldalakat , , , -vel, az és átlók metszéspontját -mel (1. ábra). 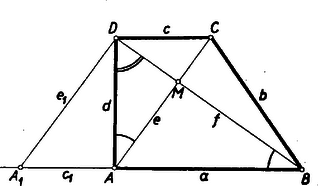 a) Igazoljuk, hogyha , akkor . Az -nál és -nél egy ívvel jelzett szögek egyenlők, mert merőleges szárú szögek, és így az és derékszögű háromszögek hasonlók. A megfelelő oldalakra ezért: b) Igazoljuk a megfordítást is, vagyis ha , akkor . Ha , akkor
II. megoldás: Helyezzük a trapézt a koordináta‐rendszerbe a 2. ábrán látható módon. A betűzést a 2. ábra mutatja. 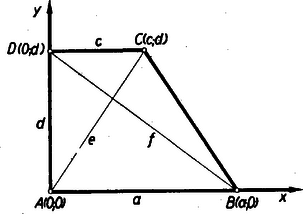 a) Az átlóegyenes iránytényezője , az átlóegyenes iránytényezője . Ha , akkor , vagyis b) Ha fennáll, hogy , akkor mindkét oldalt -vel osztva
III. megoldás: a) Toljuk el az átlót önmagával párhuzamosan úgy, hogy a szakasz -be jusson (1. ábra). Legyen , , akkor , . Ha , akkor az háromszög derékszögű, és magasságára felírhatjuk, hogy b) Legyen most , és emeljünk -ben -re merőleges -et, amely az oldal meghosszabbítását -ben metszi. . Ezzel az derékszögű háromszöget állítottuk elő. Ebben . De a feltétel szerint úgy, hogy
|