Kezdőlap


Feladat:	2009. évi Nemzetközi Fizika Diákolimpia 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2009/október, 432 - 435. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Csillagok jellemzői, Csillagfejlődés
Hivatkozás(ok):	Feladatok megoldásai: 2009/november: 2009. évi Nemzetközi Fizika Diákolimpia 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

3. feladat. Miért olyan nagyok a csillagok?

A csillagok forró gázgömbök, melyek ragyogását a belsejükben lezajló magfúzió adja. Leggyakoribb esetben e folyamat során hidrogénből hélium keletkezik. Ebben a problémában klasszikus mechanikai, illetve kvantummechanikai fogalmak, valamint elektrosztatikai, termodinamikai összefüggések segítségével keressük a választ arra a kérdésre, hogy a gázgömbnek miért csak egy bizonyos mérete fölött indul be a fúziós reakció. Sőt, a hidrogén fúziójához szükséges kritikus tömeg és sugár értékét is meghatározzuk. (A Napról, mint csillagról látható kép a hátsó belső borítón jobbra középen.)
Fontos fizikai állandók:
gravitációs állandó:

G = 6, 7 \cdot 10^{- 11} m^{3} {kg}^{- 1} s^{2}

;
Boltzmann-állandó:

k = 1, 4 \cdot 10^{- 23} {J K}^{- 1}

;
Planck-állandó:

h = 6, 6 \cdot 10^{- 34} m^{2} {kg s}^{- 1}

;
proton tömege:

m_{p} = 1, 7 \cdot 10^{- 27}

kg;
elektron tömege:

m_{e} = 9, 1 \cdot 10^{- 31}

kg;
elemi töltés:

q = 1, 6 \cdot 10^{- 19}

C;
vákuum permittivitás:

ε_{0} = 8, 9 \cdot 10^{- 12} C^{2} N^{- 1} m^{- 2}

;
Nap sugara:

R_{N} = 7, 0 \cdot 10^{8}

m;
Nap tömege:

M_{N} = 2, 0 \cdot 10^{30}

kg.

1. Csillagok központi hőmérsékletének klasszikus becslése
Tegyük föl, hogy a csillagot formáló gáz tiszta ionizált hidrogén, azaz elektronok és protonok azonos arányú keveréke, mely ideális gázként viselkedik. A klasszikus fizika törvényei szerint két proton fúziójához az szükséges, hogy

10^{- 15}

méternél közelebb kerüljenek egymáshoz, mivel csak ilyen kis távolság esetén válik a rövidtávú magerő meghatározóvá. Azonban ahhoz, hogy ilyen közel kerüljenek egymáshoz, le kell győzniük a Coulomb-taszítást. Tegyük fel, hogy két klasszikus, pontszerű részecskének tekintett proton

v_{rms}

nagyságú, egymással ellentétes irányú sebességgel halad egymás felé egy egyenes mentén, és frontálisan ütközik. Itt

v_{rms}

a termodinamikai átlagsebesség (sebességnégyzet átlagának a gyöke; az index az angol root-mean-square kifejezésre utal).
1.a. Határozd meg azt a kritikus

T_{c}

hőmérsékletet, amely esetén két ütköző proton közti minimális

d_{c}

távolság éppen

10^{- 15}

m! A keresett értéket, és ebben a feladatban minden további számszerű eredményt két értékes jegyre adj meg!

2. Annak igazolása, hogy az előző hőmérséklet-becslés hibás
Ahhoz, hogy ellenőrizzük előző becslésünk megbízhatóságát, még egy független módszerre van szükségünk a csillagok központi hőmérsékletének meghatározására. Egy valódi csillag felépítése meglehetősen bonyolult, de néhány egyszerűsítő feltevés használatával a lényeget könnyen megérthetjük. A csillagok egyensúlyban vannak, ami azt jelenti, hogy se nem tágulnak, se nem húzódnak össze, mert a befelé mutató gravitációs erő egyensúlyt tart a kifelé mutató nyomással (6. ábra). Egy, a középponttól

r

távolságban levő gázréteg hidrosztatikai egyensúlyát a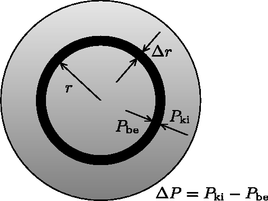

\begin{matrix} \frac{Δ P}{Δ r} = - \frac{G M_{r} ϱ_{r}}{r^{2}} \end{matrix}

egyenlet fejezi ki, ahol

P

a gáz nyomása,

G

a gravitációs állandó,

M_{r}

a csillag

r

sugarú gömbön belül eső részének tömege,

ϱ_{r}

pedig a gázréteg sűrűsége.

6. ábra. A csillagok hidrosztatikai egyensúlyban vannak, a nyomás-változással a gravitáció tart egyensúlyt

A csillag központi hőmérsékletére nagyságrendi becslést kaphatunk, ha a paramétereknek a középpontban és a csillag felszínén felvett értékét használjuk, tehát a következő közelítésekkel élünk:

\begin{matrix} Δ P \approx P_{0} - P_{c}, \end{matrix}

ahol

P_{c}

a központi,

P_{0}

pedig a felületi nyomás. Mivel

P_{c} ≫ P_{0}

, feltehetjük, hogy

\begin{matrix} Δ P \approx - P_{c} . \end{matrix}

Ugyanezzel a közelítéssel élve, a ,,rétegvastagságra'' az adódik, hogy

\begin{matrix} Δ r \approx R, \end{matrix}

ahol

R

a csillag (teljes) sugara, valamint

\begin{matrix} M_{r} \approx M_{R} = M, \end{matrix}

ahol

M

a csillag teljes tömege.
A sűrűség közelíthető a középpontban felvett értékével,

\begin{matrix} ϱ_{r} \approx ϱ_{c} . \end{matrix}

Feltehetjük továbbá, hogy a nyomás az ideális gáztörvényből számolható.
2.a. Határozd meg a csillag középpontjában a

T_{c}

hőmérsékletet kizárólag a csillag sugarának, tömegének, valamint fizikai állandóknak a segítségével!
A fenti modell teszteléséhez vizsgáljuk meg a kapott eredmény egy egyszerű következményét:
2.b. A 2.a. pontban kapott egyenlőség alapján add meg a vizsgált csillagokra az

M / R

arány becsült értékét kizárólag fizikai állandók és

T_{c}

függvényében!
2.c. A

T_{c}

hőmérsékletnek az 1.a. pontban meghatározott értéke alapján határozd meg számszerűen a csillagok

M / R

arányának jósolt értékét!
2.d. Most számold ki a Nap esetén az

M_{Nap} / R_{Nap}

arányt, és ellenőrizd, hogy ez az érték sokkal kisebb, mint a 2.c. pontban meghatározott érték!

3. Csillagok központi hőmérsékletének kvantummechanikai becslése
A 2.d. pontban talált nagy eltérés azt sejteti, hogy

T_{c}

-nek az 1.a. pontban adott becslése nem helyes. Az ellentmondás kvantummechanikai effektusok figyelembevételével oldható fel. Eszerint a protonok hullámként viselkednek, és egyetlen proton a

λ_{p}

de Broglie-hullámhosszával azonos nagyságrendű területen ,,van szétkenve''. Ez azt jelenti, hogy ha a protonok között elért

d_{c}

minimális távolság a

λ_{p}

hullámhossz közelébe esik, akkor a két részecske kvantummechanikai értelemben ,,átfedésbe kerül'', és így képesek a fúzióra.
3.a. Feltéve, hogy a

v_{rms}

sebességgel haladó protonok esetén a fúzió feltétele

d_{c} = \frac{λ_{p}}{2^{1 / 2}}

, határozd meg

T_{c}

értékét csupán fizikai állandók segítségével!
3.b. Határozd meg a

T_{c}

hőmérsékletre a 3.a. pontban kapott kifejezés numerikus értékét!
3.c. A 3.b. pontban kapott érték valamint a 2.b. pontban levezetett kifejezés segítségével határozd meg az

M / R

arány becsült numerikus értékét csillagokra! Ellenőrizd, hogy ez az érték közel esik-e a megfigyelésekből származó

M_{Nap} / R_{Nap}

arányhoz!
Valóban, az úgynevezett fősorozatba eső csillagok (melyekben hidrogén fúziója zajlik, ,,normális'' csillagok) nagyon tág tömeghatárok között megfelelnek a fenti becslésnek.

4. Csillagok tömeg/sugár aránya
Az előző feladatban tapasztalt egyezés azt sejteti, hogy a Nap középponti hőmérsékletének becslésére a kvantummechanikai gondolatmenet helyes.
4.a. Az előző eredményt felhasználva mutasd meg, hogy minden olyan csillag esetén, melyben hidrogén-fúzió zajlik, az

M

tömeg és

R

sugár aránya állandó, mely kizárólag univerzális fizikai konstansoktól függ! Határozd is meg ezt az

M / R

arányt ezekre a csillagokra!

5. A legkisebb csillagok tömege és sugara
A 4.a. pontban kapott eredményből arra következtethetnénk, hogy bármely tömeggel létezhetnek hidrogén-fúziós ciklusban levő csillagok, feltéve, hogy az összefüggés feltétele teljesül. Ez a következtetés azonban helytelen.
A hidrogén-fúziós ciklusban levő csillagokban található gáz ideális gázként viselkedik. Ez azt jelenti, hogy az elektronok közti

d_{e}

tipikus távolság átlagos értéke nagyobb, mint az elektronok

λ_{e}

de Broglie-hullámhossza. Ellenkező esetben ugyanis az elektronok egy úgynevezett degenerált állapotban lennének, és a csillag másképp viselkedne. Felhívjuk a figyelmet arra a tényre, hogy a vizsgált csillag-típusban levő protonokat és elektronokat másként kezeljük. Protonok esetén a de Broglie-hullámok átfedése szükséges ahhoz, hogy a fúzió létrejöhessen, míg elektronok esetén a de Broglie hullámok nem fedhetnek át, mert különben az elektronokat nem kezelhetnénk ideális gázként.
A valóságban a csillagok belsejében levő gáz sűrűsége a középpont felé haladva nő. Ennek ellenére ebben a nagyságrendi becslésben tegyük föl, hogy a vizsgált csillag sűrűsége állandó. Ezen kívül felhasználhatjuk, hogy

m_{p} ≫ m_{e}

.
5.a. Határozd meg az

n_{e}

átlagos elektronszám-sűrűséget a csillag belsejében!
5.b. Határozd meg az elektronok közti

d_{e}

tipikus távolságot a csillag belsejében!
5.c. A

d_{e} \geq \frac{λ_{e}}{2^{1 / 2}}

feltétel használatával határozd meg egyenlettel a legkisebb olyan csillag sugarát, mely hidrogén-fúziós ciklusban lehet! (Ezek az ún. normál csillagok.) Tekintsd úgy, hogy a csillag középpontjában mért hőmérséklet a csillagban bárhol mérhető hőmérséklet tipikus értéke.
5.d. Határozd meg a lehető legkisebb normál csillag sugarának számértékét méterben is és a Nap sugarának (rádiuszának) egységében is!
5.e. Határozd meg a lehető legkisebb normál csillag tömegének számértékét kilogrammban is, és Naptömeg-egységben is!

6. Hélium-fúzió öregebb csillagokban
Ahogy a csillagok öregednek, majdnem az összes magjukban lévő hidrogént héliummá (He) alakították, így a további fénykibocsátás érdekében arra kényszerülnek, hogy elkezdjék a hélium fuzionálását nehezebb elemekké. A hélium mag két protonból és két neutronból áll, így a töltése kétszerese, a tömege kb. négyszerese a protonénak. Láttuk korábban, hogy a proton fúziójának feltétele

d_{c} = \frac{λ_{p}}{2^{1 / 2}}

.
6.a. Add meg a megfelelő feltételt a hélium magokra vonatkozóan, és határozd meg a hélium magok

v_{rms}

(He) négyzetes átlagsebességét, valamint a hélium fúzióhoz szükséges

T

(He) hőmérsékletet!