Kezdőlap


Feladat:	2009. évi Nemzetközi Fizika Diákolimpia 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2009/október, 428 - 432. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Doppler-hatás (Doppler-effektus), Gerjesztés sugárzással (abszorpció), Indukált emisszió (lézerhatás)
Hivatkozás(ok):	Feladatok megoldásai: 2009/november: 2009. évi Nemzetközi Fizika Diákolimpia 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. feladat. Lézeres Doppler-hűtés és optikai szirupok

Ennek a feladatnak az a célja, hogy egyszerű elméleti megfontolással megértsed a ,,lézeres hűtés'' és az ,,optikai szirup'' jelenségeket. Ez azt jelenti, hogy semleges atomok (általában alkáli fémek) nyalábját egymással szemben haladó, azonos frekvenciájú lézersugarakkal hűtjük. Ezért kapott 1997-ben fizikai Nobel-díjat S. Chu, P. Phillips és C. Cohen-Tannoudji.
A hátsó belső borító jobb felső képe nátrium atomokat ábrázol (a fényes pont középen), melyek három, egymásra merőleges lézersugár-pár kereszteződésében vannak csapdázva. A csapda területét szokás ,,optikai szirup''-nak (,,optical molasses'') nevezni, mivel a disszipatív optikai erő a szirupon áthaladó testekre ható viszkózus erőre emlékeztet.
Ebben a feladatban egy foton és egy atom egyszerű kölcsönhatását és a disszipációs mechanizmust fogod vizsgálni egy dimenzióban.

I. rész: A lézeres hűtés alapjai
Tekints egy

m

tömegű atomot, amely a

+ x

irányban,

v

sebességgel mozog. Az egyszerűség kedvéért vizsgáld a problémát egy dimenzióban, azaz ne foglalkozz az

y

és

z

irányokkal (4. ábra). Az atomnak két belső energiaszintje van. Az alapállapot energiáját nullának tekintjük, a gerjesztett állapot energiája pedig

ℏ ω_{0}

, ahol

ℏ = h / 2 π

. Az atom kezdetben alapállapotban van. Egy lézersugár, melynek a laboratórium koordináta-rendszerében mért körfrekvenciája

ω_{L}

, a

- x

irányban halad, és ütközik egy atommal. Kvantummechanikai szempontból a lézersugár nagyszámú egyforma fotonból áll, melyek energiája

ℏ ω_{L}

és impulzusa

- ℏ q

. A fotont elnyelheti egy atom, amely azt később spontán kibocsátja; ez a kibocsátás (emisszió) azonos valószínűséggel történhet a

+ x

és a

- x

irányban. Mivel az atom nemrelativisztukus sebességgel mozog,

v / c ≪ 1

(ahol

c

a fénysebesség). Vedd figyelembe azt is, hogy

ℏ q / m v ≪ 1

, azaz az atom impulzusa sokkal nagyobb egy foton impulzusánál. A válaszaidban mindkét mennyiségnek csak az elsőrendű (lineáris) tagjait vedd figyelembe.

4. ábra. Egy

m

tömegű,

v

sebességű, a

+ x

irányban haladó atom, amely egy

ℏ ω_{L}

energiájú és

- ℏ q

impulzusú fotonnal ütközik. Az atomnak két belső állapota van

ℏ ω_{0}

energiakülönbséggel

Feltételezd, hogy a lézer

ω_{L}

körfrekvenciája úgy van hangolva, hogy a mozgó atom rendszeréből nézve rezonanciában van az atom belső átmenetével. Válaszolj a következő kérdésekre:

1. Elnyelés (abszorpció)
1.a. Add meg a foton elnyelésének (abszorpciójának) rezonanciafeltételét!
1.b. Add meg az atom

p_{a}

impulzusát az elnyelés után, a laboratórium rendszeréből nézve!
1.c. Add meg az atom

ε_{a}

teljes energiáját az elnyelés után, a laboratórium rendszeréből nézve!

2. Egy foton spontán kibocsátása (emissziója) a

- x

irányban
Az ütköző foton elnyelődése (abszorbciója) után valamennyi idővel az atom egy fotont bocsáthat ki (emittálhat) a

- x

irányban.
2.a. Add meg a kibocsátott foton

ε_{f}

energiáját a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.b. Add meg a kibocsátott foton

p_{f}

impulzusát a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.c. Add meg az atom

p_{a}

impulzusát a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.d. Add meg az atom

ε_{a}

teljes energiáját a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!

3. Egy foton spontán kibocsátása (emissziója) a

+ x

irányban
Az ütköző foton elnyelődése (abszorbciója) után valamennyi idővel az atom egy fotont bocsáthat ki (emittálhat) a

+ x

irányban.
3.a. Add meg a kibocsátott foton

ε_{f}

energiáját a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.b. Add meg a kibocsátott foton

p_{f}

impulzusát a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.c. Add meg az atom

p_{a}

impulzusát a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.d. Add meg az atom

ε_{a}

teljes energiáját a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!

4. Átlagos kibocsátás (emisszió) az elnyelés (abszorpció) után
A foton spontán kibocsátása egyforma valószínűséggel történhet a

- x

vagy a

+ x

irányban. Ezt figyelembe véve válaszolj a következő kérdésekre:
4.a. Add meg a kibocsátott foton

ε_{f}

átlagos energiáját az emissziós folyamat után!
4.b. Add meg a kibocsátott foton

p_{f}

átlagos impulzusát az emissziós folyamat után!
4.c. Add meg az atom

ε_{a}

átlagos teljes energiáját az emissziós folyamat után!
4.d. Add meg az atom

p_{a}

átlagos impulzusát az emissziós folyamat után!

5. Energia- és impulzusátadás
Tekints egy teljes egyfotonos elnyelési-kibocsátási (abszorpciós-emissziós) folyamatot, ahogy azt az eddigiekben tárgyaltuk. A lézersugár és az atom között egy eredő átlagos impulzus- és energiaátadás figyelhető meg.
5.a. Add meg az atom

Δ ε

átlagos energiaváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!
5.b. Add meg az atom

Δ p

átlagos impulzusváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!

6. Energia- és impulzusátadás egy

+ x

irányú lézersugárral
Tekints most egy olyan lézersugarat, amelynek

ω'_{L}

a körfrekvenciája és a

+ x

irányban halad, miközben az atom szintén a

+ x

irányban halad

v

sebességgel. Azt feltételezve, hogy az atom belső átmenete és a lézersugár között az atom rendszeréből nézve teljesül a rezonanciafeltétel, válaszolja következő kérdésekre:
6.a. Add meg az atom

Δ ε

átlagos energiaváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!
6.b. Add meg az atom

Δ p

átlagos impulzusváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!

II. rész: Disszipáció és az optikai szirup alapjai
A természetben a kvantumfolyamatokat elkerülhetetlenül bizonytalanság kíséri. Így az a tény, hogy az atom az elnyelés után véges idővel bocsát ki egy fotont, azzal a következménnyel jár, hogy a rezonanciafeltétel nem teljesül egzaktul, úgy ahogy azt eddig tárgyaltuk. Azaz a lézersugár

ω_{L}

és

ω'_{L}

körfrekvenciája bármilyen értéket felvehet, és az elnyelés (abszorpció) mégis bekövetkezhet. Az elnyelés különböző (kvantum)valószínűséggel történik, és ‐ mint ahogy azt sejteni lehet ‐ a legnagyobb valószínűséggel éppen a rezonanciafeltétel egzakt teljesülésekor. Egy foton elnyelése és kibocsátása között átlagosan eltelő időt a gerjesztett állapot élettartamának nevezzük, és így jelöljük:

Γ^{- 1}

.
Tekintsünk egy

N

atomból álló, a laboratórium koordinátarendszeréhez viszonyítva nyugalomban lévő atomhalmazt, és egy rá eső

ω_{L}

körfrekvenciájú lézersugarat. Az atomok folyamatosan fotonokat nyelnek el és bocsátanak ki, úgy, hogy átlagosan

N_{g}

atom van gerjesztett állapotban (és így

N - N_{g}

atom alapállapotban). Kvantummechanikai számítás eredményeként adódik, hogy:

\begin{matrix} N_{g} = N \frac{Ω_{R}^{2}}{{(ω_{0} - ω_{L})}^{2} + \frac{Γ^{2}}{4} + 2 Ω_{R}^{2}}, \end{matrix}

ahol

ω_{0}

az atomi átmenet rezonancia-körfrekvenciája, és

Ω_{R}

az úgynevezett Rabi-frekvencia;

Ω_{R}^{2}

arányos a lézersugár intenzitásával. Láthatod, hogy ez az érték ‐ ahogy már említettük ‐ akkor is különbözik nullától, ha

ω_{0}

nem egyezik meg a lézersugár

ω_{L}

körfrekvenciájával. Az előbbi eredményt úgy is kifejezhetjük, hogy időegységenként bekövetkező elnyelési-kibocsátási (abszorpciós-emissziós) folyamatok száma

N_{g} Γ

.
Tekintsd az 5. ábrán látható fizikai elrendezést, ahol két szemben haladó lézersugár egymással azonos, de amúgy tetszőleges

ω_{L}

körfrekvenciával ütközik az

N

atomból álló,

+ x

irányban

v

sebességgel mozgó gáznak.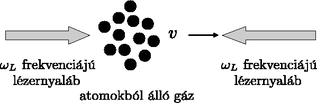

5. ábra. Két szemben haladó lézersugár egymással azonos, de amúgy tetszőleges

ω_{L}

körfrekvenciával ütközik az

N

atomból álló,

+ x

irányban

v

sebességgel mozgó gáznak

7. A lézer által az atomnyalábra kifejtett erő
7.a. Az eddigi információk alapján határozd meg azt az erőt, amit a lézersugár kifejt az atomnyalábra! Használd ki, hogy

m v ≫ ℏ q

.
8. Kissebességű határeset. Most tételezd fel, hogy az atomok sebessége elég kicsi ahhoz, hogy az erő a

v

sebesség első rendű tagjával közelíthető.
8.a. Határozd meg a 7.a. feladatban meghatározott erő kifejezését ebben a közelítésben!
Felhasználva ezt az eredményt megkeresheted annak a feltételét, hogy a lézersugár az atomnyalábot gyorsítja, lassítja, illetve nem hat rá.
8.b. Add meg annak a feltételét, hogy az erő pozitív (gyorsítja az atomokat)!
8.c. Add meg annak a feltételét, hogy az erő nulla!
8.d. Add meg annak a feltételét, hogy az erő negatív (lassítja az atomokat)!
8.e. Most tedd fel, hogy az atomok

- v

sebességgel mozognak (a

- x

irányban). Add meg annak a feltételét, hogy az erő lassítsa az atomokat!
9. Optikai szirup. Negatív erő esetében egy disszipatív súrlódó erőt kapunk. Tedd fel, hogy kezdetben, amikor

t = 0

, a gáz atomjai

v_{0}

sebességgel mozognak.
9.a. Kissebességes közelítésben határozd meg az atomok sebességét azután, hogy a lézersugarak

τ

ideje be vannak kapcsolva.
9.b. Most tételezd fel, hogy a gáz atomjai kezdetben

T_{0}

hőmérsékleten termikus egyensúlyban vannak. Határozd meg a

T

hőmérsékletet azután, hogy a lézersugarak

τ

ideje be vannak kapcsolva.
(A modell azonban nem teszi lehetővé tetszőlegesen kicsi hőmérséklet elérését.)