Kezdőlap


Feladat:	A.398	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	2006/április, 229 - 230. oldal		PDF \| MathML
Témakör(ök):	Térelemek és részeik, Algebra - Aritmetika, Nehéz feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Adott a síkon egy $k$ kör, a körön kívül fekvő $ℓ$ egyenes, továbbá a körön egy 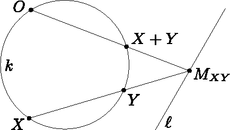$O$ pont.
Definiáljuk a $k$ kör pontjain a $+$ kétváltozós műveletet a következőképpen. A kör bármely $X$ , $Y$ pontpárjára jelöljük $M_{X Y}$ -nal $ℓ$ és az $X Y$ egyenes metszéspontját. (Ha $X = Y$ , akkor az $X Y$ egyenes az érintő. Ha a két egyenes párhuzamos, akkor $M_{X Y}$ az $ℓ$ ideális pontja.) Szerkesszük meg az $O M_{X Y}$ egyenes és a kör másik metszéspontját. (Ha $O M_{X Y}$ érinti a kört, akkor a másik metszéspont is $O$ .) Ez a pont legyen $X + Y$ .

Mutassuk meg, hogy a

+

művelet kiterjeszthető a

k

kör és az

ℓ

egyenes összes, valamint

ℓ

ideális pontjára úgy, hogy a pontok a

+

művelettel kommutatív csoportot alkossanak, amelynek egységeleme az

O

pont, azaz teljesüljenek a következő feltételek:

a)

Tetszőleges

X

Y

Z

-re

(X + Y) + Z = X + (Y + Z)

;

b)

Tetszőleges

X

Y

esetén

X + Y = Y + X

;

c)

Tetszőleges

X

-re

X + O = X

;

d)

Tetszőleges

X

-hez létezik olyan

Y

, amelyre

X + Y = O