Kezdőlap


Feladat:	2005. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2005/október, 425 - 427. oldal		PDF \| MathML
Témakör(ök):	Bolygómozgás, Kepler törvények, Mesterséges holdak, Nemzetközi Fizika Diákolimpia
Hivatkozás(ok):	Feladatok megoldásai: 2005/november: 2005. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szerencsétlenül járt műhold

A mesterséges égitestek manőverezés során leggyakrabban repülésük irányában változtatják meg sebességüket, azaz felgyorsítanak, hogy magasabb pályákra kerüljenek, vagy lefékeznek, hogy visszatérjenek a légkörbe. Ezzel szemben ebben a feladatban most kizárólag olyan pályamódosításokat vizsgálunk, melyeknek során a mesterséges égitest sugár irányú lökéssel módosítja sebességét.

A numerikus eredmények meghatározásához használd a következő értékeket: a Föld sugara

R_{T} = 6, 37 \cdot 10^{6}

m, a nehézségi gyorsulás a Föld felszínén

g = 9, 81 {m/s}^{2}

, és a sziderikus nap hosszát tekintsd

T_{0} = 24, 0

h-nak.
Tekintsünk egy

m

tömegű távközlési műholdat, mely

r_{0}

sugarú geostacionárius¹ pályán kering pontosan az Egyenlítő egy pontja fölött. A műhold manőverező hajtóművének megfelelő lökéseivel állt a pontos pályára.
Az egyes részkérdésekre kapható pontszám a feladat sorszáma után zárójelben található.
1. Kérdés.

(a)

Számold ki

r_{0}

számszerű értékét!

(b)

Add meg a műhold

v_{0}

sebességét, mint a

g

R_{T}

és

r_{0}

paraméterek függvényét, valamint határozd meg a sebesség számszerű értékét!

(c)

Határozd meg a műhold

L_{0}

perdületét (impulzusmomentumát), valamint

E_{0}

teljes mechanikai energiáját, mint a

v_{0}

m

g

és

R_{T}

paraméterek függvényét!
Amint a műhold elérte a geostacionárius pályát (lásd az F-1. ábrát), stabilizálta helyzetét, és munkára kész állapotba került, a földi irányítóközpont hibájának következtében a menőverező hajtómű rövid időre újra bekapcsolódott. A hajtómű a műholdat a Föld irányába lökte meg, és annak ellenére, hogy a földi irányítóközpont szinte azonnal reagált, és kikapcsolta a hajtóművet, a műhold sebessége egy nem kívánt

Δ v

értékkel módosult. A lökést a

β = Δ v / v_{0}

lökési paraméterrel jellemezzük. A manőver időtartama jóval rövidebb, mint a műhold keringésének bármilyen más jellemző ideje, tehát a lökés pillanatszerűnek tekinthető.

F-1. ábra

2. Kérdés. Tegyük föl, hogy

β < 1

.
2.1. Határozd meg az új pályát jellemző mennyiségeket², azaz a pálya poláris egyenletében szereplő

l

paramétert (semi-latus-rectum = ,,fél-merőleges-távolság'') és az

ε

excentricitást az

r_{0}

és

β

paraméterek függvényében!
2.2. Határozd meg az új pálya főtengelye és a véletlen pályamódosítás helyvektora közti

α

szöget! (A helyvektor kezdőpontja a Föld középpontja.)
2.3. Határozd meg a pálya földközeli, illetve földtávoli pontjának

r_{{min}_{}^{}}

, illetve

r_{{max}_{}^{}}

távolságát a Föld középpontjától, mint az

r_{0}

és

β

paraméterek függvényét, valamint add meg a kifejezések számszerű értékét

β = 1 / 4

esetén!
2.4. Határozd meg a módosult pálya

T

keringési idejét, mint a

T_{0}

és

β

paraméterek függvényét, és add meg a keringési idő számszerű értékét

β = 1 / 4

esetén!
3. Kérdés.
3.1. Határozd meg azt a legkisebb

β_{esc}

lökési paramétert, amely mellett a műhold elhagyja a Föld gravitációs terét!
3.2. Ebben az esetben határozd meg a műhold pályájának a Földet legjobban megközelítő pontjának

r'_{{min}_{}^{}}

távolságát a Föld középpontjától, mint az

r_{0}

paraméter függvényét!
4. Kérdés. Tegyük föl, hogy

β > β_{esc}

.
4.1. Határozd meg a

v_{0}

és

β

paraméterek függvényeként, hogy mekkora

v_{\infty}

sebessége marad a műholdnak, ha végtelen messzire eltávolodik a Földtől!
4.2. Határozd meg a végtelen távoli mozgást jellemző

b

,,impakt paramétert'', mint az

r_{0}

és

β

paraméter függvényét! (Lásd: F-2. ábra.)

F-2. ábra

4.3. Határozd meg a végtelen távoli mozgás irányának

ϕ

szögét, mint a

β

paraméter függvényét! (Lásd: F-2. ábra.) Add meg a szög számszerű értékét a

β = \frac{3}{2} β_{esc}

esetre!
Segítség. A távolság négyzetének reciprokával csökkenő, centrális erőtérben mozgó testek ellipszis, parabola vagy hiperbola pályán mozognak. Az

m ≪ M

közelítés mellett a centrális gravitációs teret létrehozó

M

tömeg a pálya egyik fókuszában van. A koordináta-rendszer kezdőpontját ebben a pontban felvéve, a fenti pályák általános, polárkoordinátás egyenlete (lásd: F-3. ábra)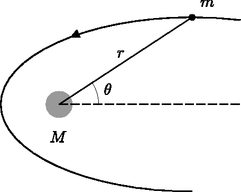

\begin{matrix} r (θ) = \frac{l}{1 - ε cos θ} \end{matrix}

alakú, ahol az

l

pozitív állandó a görbe paramétere (semi-latus-rectum = fél-merőleges-távolság),

ε

pedig a pálya excentriciása. A mozgást jellemző megmaradó mennyiségekkel kifejezve:

\begin{matrix} l = \frac{L^{2}}{G M m^{2}} és ε = {(1 + \frac{2 E L^{2}}{G^{2} M^{2} m^{3}})}^{1 / 2}, \end{matrix}

ahol

G

a gravitációs állandó,

L

a keringő test perdületének (impulzusmomentumának) nagysága a középpontra vonatkoztatva,

E

pedig a mechanikai energiája. (A potenciális energia zéruspontja a végtelenben van.)

F-3. ábra

A következő három esetet különböztethetjük meg:

i)

0 \leq ε < 1

, a görbe ellipszis (

ε = 0

esetén kör).

i i)

ε = 1

, a görbe parabola.

i i i)

ε > 1

, a görbe hiperbola.

¹A pályához tartozó keringési idő

T_{0}

²Nézd át a feladat végén található ,,segítséget''!