Cím:	Séta a havon ‐ az ezerarcú feladat 3.
Szerző(k):	Besenyei Ádám
Füzet:	2017/január, 2 - 7. oldal	PDF  |  MathML
Hivatkozás(ok):	2016/november: Séta a havon ‐ az ezerarcú feladat 1. 2016/december: Séta a havon ‐ az ezerarcú feladat 2.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   7. Egy geometriai nagyágyú Az eddigi temérdek analízis és algebra után következzen most egy geometriai okoskodás, amelynek ötlete a [10] cikkből származik és egy ‐ a versenyfeladatokon edződöttek számára vélhetően jól ismert ‐ nevezetes geometriai egyenlőtlenségre támaszkodik. (Az alábbiakban kissé pongyolán sokszög oldalának mérőszáma helyett egyszerűen az oldalról fogunk beszélni.)   7.1. tétel (Ptolemaiosz-egyenlőtlenség) A síkon bármely konvex négyszögben a szemközti oldalak szorzatának összege legalább akkora, mint az átlók szorzata. Egyenlőség csakis húrnégyszögben teljesül.   Bizonyítás. Tekintsük a 9. ábrán látható $ABCD$ konvex négyszöget, amelynek oldalai $AB=a$, $BC=b$, $CD=c$, $DA=d$, az átlói pedig $AC=e$, $BD=f$. Ekkor azt kell igazolnunk, hogy $\begin{array}{c}{\displaystyle ac+bd\ge ef\mathrm{.}}\end{array}$ Emeljünk a $BC$ oldalra a $CDA$ háromszöggel hasonló $CBE$ háromszöget úgy, hogy $ACD\sphericalangle =ECB\sphericalangle$ és $CDA\sphericalangle =CBE\sphericalangle$ (más szóval alkalmazzunk $C$ középpontú forgatva nyújtást az $ACD$ háromszögre úgy, hogy $CD$ képe $CB$ legyen). A hasonlóság aránya $CB/CD=b/c$, ezért $CE=\frac{b}{c}e$ és $BE=\frac{b}{c}d$. Vegyük észre, hogy ekkor a $CAE$ és $CDB$ háromszögek szintén hasonlók, mert $BCD\sphericalangle =ECA\sphericalangle$ és $CE/CB=CA/CD=e/c$. Következésképpen $AE/DB=e/c$, vagyis $AE=\frac{e}{c}f$. Mivel az $ABE$ háromszögben az $AB$ és $BE$ oldalak összege legalább akkora, mint $AE$, így $\begin{array}{c}{\displaystyle a+\frac{b}{c}d\ge \frac{e}{c}f\mathrm{,}}\end{array}$ amiből $c$-vel való beszorzás után éppen a bizonyítandó egyenlőtlenség adódik. Egyenlőség pontosan akkor áll fenn, ha az $ABE$ háromszög elfajuló, azaz $ABC\sphericalangle +CBE\sphericalangle ={180}^{\circ }$. Ez azt jelenti, hogy az $ABCD$ négyszögben a $B$ és $D$ csúcsoknál lévő belső szögek összege ${180}^{\circ }$, tehát $ABCD$ húrnégyszög. 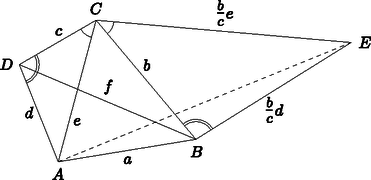 $\square$   9. ábra     7.2. történeti megjegyzés. Klaudiosz Ptolemaiosz a Kr. e. II. századi Alexandriában élt matematikus, csillagász, földrajztudós, a geocentrikus ‐ a Földet a világegyetem középpontjának tekintő ‐ világkép megalkotója. Az Almageszt című műve az ókori csillagászat legfontosabb tudományos forrása, amely a benne található trigonometriai számítások szempontjából is kiemelkedő jelentőségű. Ebben igazolta Ptolemaiosz többek között azt, hogy húrnégyszögben az átlók szorzata a szemközti oldalak szorzatainak összege.   7.3. megjegyzés. E kicsit talán hosszabb lélegzetvételűre nyúló megjegyzésben a Ptolemaiosz-egyenlőtlenség bizonyítása kapcsán hívjuk fel a figyelmet néhány észrevételre, általánosításra. Első olvasáskor nyugodtan a hómezős feladat megoldásához lehet ugrani. Az előbbi bizonyítás apró finomításával nem nehéz igazolni (lásd [5, 12.14. feladat]), hogy tetszőleges $A$, $B$, $C$, $D$ síkbeli pontnégyesre igaz $\begin{array}{c}{\displaystyle AB\cdot CD+BC\cdot DA\ge AC\cdot BD\mathrm{,}}\end{array}$ ahol egyenlőség pontosan akkor teljesül, ha a négy pont egy körön (vagy egyenesen) helyezkedik el és azon az $AC$ pontpár elválasztja a $BD$ pontpárt. Sőt, megmutatható, hogy bármely nem egy síkban fekvő pontnégyes esetén szigorú egyenlőtlenség áll fenn (erről lásd a [12] könyv 5.8. szakaszát). A Ptolemaiosz-egyenlőtlenségnek a fentitől különböző, a Simson-egyenes bizonyos tulajdonságára épülő bizonyítása olvasható a [2] könyvben. Számos feladat között böngészhetünk a [6] írásban, ahol az egyenlőtlenség egy általánosítása $-$ a Casey-tétel, amelyben a csúcsok szerepét érintő körök, az oldalakét pedig érintők veszik át $-$ ugyancsak terítékre kerül. Végül nem tudunk ellenállni a kísértésnek, hogy röviden szót ejtsünk a Ptolemaiosz-egyenlőtlenség komplex számok segítségével történő igen elegáns igazolásáról. Tekintsük az $A$, $B$, $C$, $D$ pontoknak megfelelő $\text{a}$, $\text{b}$, $\text{c}$, $\text{d}$ komplex számokat a komplex számsíkon (lásd 10. ábra), azaz például $\text{a}=a_1+a_2\text{i}$, ahol $a_1$ a valós, $a_2$ pedig a képzetes rész. 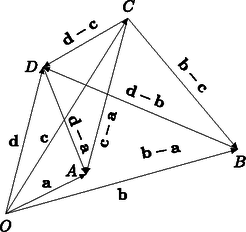  10. ábra   A komplex számok közötti szorzás a valós számok szorzásához hasonlóan viselkedik ${\text{i}}^2=-1$ figyelembevételével: $\begin{array}{c}{\displaystyle \text{a}\cdot \text{b}=\left(a_1+a_2\text{i}\right)\left(b_1+b_2\text{i}\right)=a_1{b}_1-a_2{b}_2+\left(a_1{b}_2+a_2{b}_1\right)\text{i}\mathrm{.}}\end{array}$ Induljunk ki most a könnyen ellenőrizhető $\begin{array}{c}{\displaystyle \left(\text{a}-\text{c}\right)\cdot \left(\text{b}-\text{d}\right)=\left(\text{a}-\text{d}\right)\cdot \left(\text{b}-\text{c}\right)+\left(\text{d}-\text{c}\right)\cdot \left(\text{b}-\text{a}\right)}\end{array}$ (7.1) azonosságból. Vegyük észre (ismét lásd a 10. ábrát), hogy $\text{a}-\text{c}$ és $\text{b}-\text{d}$ az $\overrightarrow{AC}$, $\overrightarrow{DB}$ átlóvektorok, továbbá $\text{a}-\text{d}$ és $\text{b}-\text{c}$, illetve $\text{d}-\text{c}$ és $\text{b}-\text{a}$ rendre a $\overrightarrow{DA}$ és $\overrightarrow{CB}$, illetve $\overrightarrow{CD}$ és $\overrightarrow{AB}$ szemközti oldalvektorok. Ekkor (7.1) mindkét oldalán abszolút értékét véve, majd alkalmazva a háromszög-egyenlőtlenséget: $\begin{array}{c}{\displaystyle |\text{a}-\text{c}|\cdot |\text{b}-\text{d}|\le |\text{a}-\text{d}|\cdot |\text{b}-\text{c}|+|\text{d}-\text{c}|\cdot |\text{b}-\text{a}|\mathrm{,}}\end{array}$ ami éppen a Ptolemaiosz-egyenlőtlenség. Az egyenlőség esetét egyáltalán nem nyilvánvaló kiolvasni a bizonyításból, ebben az úgynevezett kettősviszony segíthet, bővebben lásd például [11, 31. feladat], [12, 12.5. szakasz], ahol a komplex számok egyéb geometriai alkalmazásáról is olvashatunk.   A hómezős feladat megoldása. Ennyi előkészület után térjünk vissza a hómezős feladat megoldására, most a Ptolemaiosz-egyenlőtlenség segítségével. Tekintsük a 11. ábrát, ahol legyen $D^{*}$ a $BC$ szakasz azon pontja, amelyre $BA{D}^{*}\sphericalangle ={30}^{\circ }$ (a korábbiak fényében tudjuk, hogy ez fogja adni a minimumot). Rajzoljuk meg az $A$, $D^{*}$ és $C$ pontokon átmenő kört, amelynek középpontja legyen $O$, sugara pedig $r$, és a $D^{*}$ pontban a $BC$ szakaszra állított merőleges egyenes messe a kört az $M$ pontba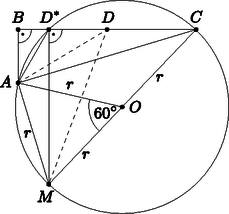n.   11. ábra   A Thalész-tétel miatt ekkor $MC$ átmérő a körben, tehát $MC=2r$. Másrészt a kerületi és középponti szögek tétele miatt $\begin{array}{c}{\displaystyle MOA\sphericalangle =2M{D}^{*}A\sphericalangle =2BA{D}^{*}\sphericalangle ={60}^{\circ }}\end{array}$ ($BA{D}^{*}\sphericalangle$ és $M{D}^{*}A\sphericalangle$ fordított állásúak), vagyis az $MOA$ egyenlő szárú háromszög szabályos, így $AM=r$. Ha $D$ a $BC$ szakasz tetszőleges pontja, akkor az $AMCD$ konvex négyszögben a Ptolemaiosz-egyenlőtlenség szerint $\begin{array}{c}{\displaystyle AD\cdot MC+AM\cdot DC\ge AC\cdot MD\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle 2r\cdot AD+r\cdot DC\ge AC\cdot MD\mathrm{.}}\end{array}$ Minthogy $M{D}^{*}$ átfogó az $MD{D}^{*}$ (esetleg elfajuló) derékszögű háromszögben, ezért $MD\ge M{D}^{*}$, így $\begin{array}{c}{\displaystyle AD+\frac{DC}{2}\ge \frac{AC\cdot M{D}^{*}}{2r}\mathrm{,}}\end{array}$ ahol a jobb oldal a $D$ pont választásától független állandó. Egyenlőség pontosan akkor van, ha $ADMC$ húrnégyszög, vagyis $D=D^{*}$. Ezzel sokadjára beláttuk, hogy az (1.2) kifejezés minimumhelyét a $D^{*}$ pont adja, tehát a gyalogosnak itt kell kimennie az országútra. Akiknek elnyerte tetszését a húrnégyszögek világa, azok a [3] könyvben indulhatnak a meghódításukra, ezenkívül pedig ajánljuk a szakaszban már korábban említett [2, 6, 11, 12] olvasnivalókat.   8. Besegít a mechanika Zárásként a hómezős feladatot mechanikai köntösbe bújtatjuk, amelynek ötlete Pólya György ‐ világhírű matematikus, a matematikai gondolkodás és problémamegoldás tudományának kiemelkedő tanár- és tudósegyénisége ‐ [9] könyvének 9. fejezetében is szerepel, ahol számos egyéb szélsőérték-feladat fizikai szemléletű megoldása olvasható élvezetes stílusban. Képzeljük el, hogy a 12. ábrán látható módon a vízszintes helyzetű $BC$ (tökéletesen merev) rúdra felfűzve szabadon (súrlódásmentesen) csúszhat a $D$ gyűrű. A gyűrűhöz egy $DAP={\ell }_1$ és egy $DCQ={\ell }_2$ (elegendő) hosszúságú (nyújthatatlan) kötelet kötünk, amelyeket rendre az $A$ és $B$ pontokban rögzített csigákon átvetünk, majd ezután a $P$, illetve $Q$ végükre egy $p$, illetve $q$ súlyú testet helyezünk, ahol a súlyok arányát később választjuk meg. (A szokásos módon a gyűrűt, a csigákat és a súlyokat is pontszerűnek tekintjük, a kötél súlyát és a súrlódást pedig elhanyagoljuk.) 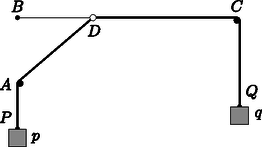  12. ábra   Magára hagyva a rendszert egy idő után beáll az egyensúlyi helyzetébe, amelyben a helyzeti energiája minimális. A $BC$ rudat véve a viszonyítási szintnek a $p$ súlyú test $\left(-BP\right)$ magasságban található, ezért a helyzeti energiája $\left(-BP\cdot p\right)$; ehhez hasonlóan a $q$ súlyú test helyzeti energiája $\left(-CQ\cdot q\right)$. A rendszer helyzeti energiája tehát a $BP\cdot p+CQ\cdot q$ kifejezés ellentettje, amely akkor lesz a lehető legkisebb, ha $BP\cdot p+CQ\cdot q$ maximális. Minthogy $BP=BA+AP$ és $AP={\ell }_1-AD$, $CQ={\ell }_2-DC$, ezért ${\displaystyle \begin{array}{cc}\hfill {\displaystyle BP\cdot p+CQ\cdot q}& {\displaystyle =BA\cdot p+\left({\ell }_1-AD\right)\cdot p+\left({\ell }_2-DC\right)\cdot q=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left({\ell }_{1}p+{\ell }_{2}q+BA\cdot p\right)-\left(AD\cdot p+DC\cdot q\right)\mathrm{.}}\hfill \end{array}}$ Itt az ${\ell }_{1}p+{\ell }_{2}q+BA\cdot p$ mennyiség állandó, így egyensúlyi helyzetben az $\begin{array}{c}{\displaystyle AD\cdot p+DC\cdot q}\end{array}$ kifejezés minimális. Ha most a súlyok arányát úgy választjuk meg, hogy $q=p/2$, akkor a $\begin{array}{c}{\displaystyle p\cdot \left(AD+\frac{DC}{2}\right)}\end{array}$ kifejezés minimumhelye adja egyensúly esetén a $D$ pont helyzetét. De ez (1.1) alapján éppen megegyezik a hómezős feladatbeli út megtételéhez szükséges idővel, ha $p=1/v$. Így tehát a mechanikai problémabeli egyensúlyi helyzet megfelel a hómezős feladat időben legrövidebb útjának. Szerencsére a mechanikai rendszer egyensúlyi helyzetét nemcsak energiákkal, hanem a gyűrűre ható erők eredőjének segítségével szintén jellemezhetjük, ezáltal a minimumhely egy másik leírását nyerjük. Tudjuk, hogy egyensúlyi helyzetben a gyűrűre ható erők kiegyenlítik egymást. Mivel a súlyok húzását a kötelek és a csigák változatlanul közvetítik, ezért a gyűrűre egy $p$ és egy $p/2$ nagyságú erő hat a két kötél irányában, lásd a 13. ábrát. A gyűrű nyugalomban van, így ezen két erő vízszintes összetevői semlegesítik egymást (függőlegesen pedig a rúd merevségéből származó erő ellensúlyozza a $p$ nagyságú erő hatását). Ha $ADB\sphericalangle =\delta$, akkor az $A$ csiga irányában ható erő vízszintes kompenense $p\text{cos}\delta$ nagyságú. A $B$ csiga irányában a vízszintes $p/2$ nagyságú erő hat, így szükségképpen $\begin{array}{c}{\displaystyle \frac{p}{2}=p\text{cos}\delta \mathrm{,}}\end{array}$ vagyis $\text{cos}\delta =1/2$, tehát $\delta ={60}^{\circ }$. Ez azt jelenti, hogy egyensúlyi helyzetben $ADB\sphericalangle ={60}^{\circ }$, és az előbb meggondoltak tükrében a hómezős feladatban szintén ez a $D$ pont szolgáltatja az időben legrövidebb utat. 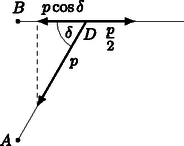  13. ábra   A fizika matematikai alkalmazásaira további meglepő példákat láthatunk a [8] könyvben, ahol a hómezős feladat optikai és mechanikai megközelítéséről is bővebben olvashatunk. Ajánljuk továbbá az [1] cikket, amely elektromos ellenállások hálózatait hívja segítségül különböző egyenlőtlenségek, köztük a számtani és harmonikus közép közötti egyenlőtlenség igazolásához.     9. Irány Kukutyin és Piripócs A cikk elején beharangozott megoldások sora véget ért, de a lehetséges okoskodások tárháza alighanem kimeríthetetlen. Érdemes tovább keresgélni és a közöttük lévő kapcsolatokat feltérképezni, valamint megvizsgálni, mi a helyzet abban az esetben, ha a gyalogos sebessége $c$-szer ($c>0$) akkora az országúton, mint a hómezőn (az országúton akár lassabban is mehet). Egy általánosítási lehetőség az érdeklődő és elszánt Olvasók számára a következő.   Feladat. Kukutyin és Piripócs egy egyenes autópálya két különböző oldalán helyezkedik el (lásd 14. ábra). Az autópálya egy $M$ pontjából leágazásokat építenek a két városhoz. Az építési költség Kukutyin felé $c$-szer akkora, mint Piripócs felé (ahol $c>0$). Hol legyen az $M$ pont, hogy az útépítés összköltsége minimális legyen? 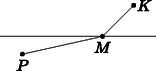  14. ábra     A $c=1$ eset megoldása nyilvánvaló, mert ekkor a $PK$ szakasz hosszban a legrövidebb, tehát a költsége minimális. Ez a feladat függvénytani álruhában a márciusi emelt szintű feladatsor 4. feladata volt (és például a 2009/2010-es tanévi Arany Dániel Matematikai Tanulóversenyen a kezdők I‐II. kategória második fordulójában is szerepelt, a megoldásában a (6.2) egyenlőtlenség ugyancsak felbukkant, lásd a feladatsort és a megoldást a [13] weboldalon). Próbáljunk meg a hómezős feladatnak a KöMaL áprilisi számában és e cikkben közölt megoldásai közül minél többet a fenti feladatra általánosítani. Ezek közül a differenciálszámítást használó okoskodás olvasható a [7] könyv 11.49. Példájában; a mechanikai érvelés a [9] könyv 9. fejezetében; a Ptolemaiosz-tételre épülő megoldás a [10] cikkben; a Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenséget alkalmazó pedig a [4] cikkben, ahol ezenfelül egy, a fény hullámtermészete által motivált, Huygenstől eredő geometriai megoldás is található. Izgalmas kalandozást kívánunk az ötletek rengetegében!   Köszönetnyilvánítás. A szerző köszönettel tartozik Kovács Balázsnak és Gnädig Péternek a kézirathoz fűzött értékes megjegyzéseikért.     Hivatkozások [1] Besenyei Ádám, A Milne-egyenlőtlenség és társai, avagy ellenállások álruhában I‐II., KöMaL, 2015/9, 514‐524. és 2016/1, 2‐10., http://abesenyei.web.elte.hu/publications/ellenallas.pdf. [2] H. S. M. Coxeter, S. L. Greitzer, Az újra felfedezett geometria, Gondolat, Budapest, 1977. [3] Gerőcs L., A húrnégyszögek meghódítása, Akadémiai Kiadó, Budapest, 2010. [4] M. Golomb, Elementary Proofs for the Equivalence of Fermat's Principle and Snell's Law, Amer. Math. Monthly, Vol. 71, No. 5 (May, 1964), 541‐543., http://www.jstor.org/stable/2312599. [5] Hraskó András, Surányi László (szerk.), Geometria, 9‐10. évfolyam, Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 2013., http://matkonyv.fazekas.hu/cache/pdf/vol_geometria_ii.pdf. [6] Kubatov Antal, Ptolemaios tétele, Casey-tétel, feladatok, http://matekold.fazekas.hu/portal/tanitasianyagok. [7] Laczkovich Miklós, T. Sós Vera, Valós Analízis I., TypoTeX, Budapest, 2012. [8] M. Levi, The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, Princeton, New Jersey, 2009. [9] Pólya György, Indukció és analógia (A matematikai gondolkodás művészete 1.), Gondolat, Budapest, 1988. [10] D. Pedoe, A Geometric Proof of the Equivalence of Fermat's Principle and Snell's Law, Amer. Math. Monthly, Vol. 71, No. 5 (May, 1964), 543‐544., http://www.jstor.org/stable/2312600. [11] Reiman István, Geometriai feladatok megoldása a komplex számsíkon, 3. kiadás, Középiskolai Szakköri Füzetek, Tankönyvkiadó, Budapest, 1972. [12] Reiman István, Geometria és határterületei, Szalay Könyvkiadó és Kereskedőház Kft., 1999. [13] http://www.eszesen2010.hu.