Cím:	Séta a havon ‐ az ezerarcú feladat 2.
Szerző(k):	Besenyei Ádám
Füzet:	2016/december, 514 - 521. oldal	PDF  |  MathML
Hivatkozás(ok):	2016/november: Séta a havon ‐ az ezerarcú feladat 1. 2017/január: Séta a havon ‐ az ezerarcú feladat 3.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   4. A gyalogosok és Huygens Térjünk most vissza a 2. szakasz eredményének elemzésére, ezáltal az időben legrövidebb út egy figyelemre méltó tulajdonságát fogjuk felfedni.   Fél szabályos háromszögek. Tanulmányozzuk először azt, hogy geometriailag milyen speciális helyzetű az időben legrövidebb út, amelyben a $D$ pontnak $\sqrt[]{3}$ km távolságra kell lennie $B$-től. A Pitagorasz-tétel szerint ekkor $AD=2\sqrt[]{3}=2BD$, így az $ADB$ háromszög éppen egy szabályos háromszög fele, vagyis $ADB\sphericalangle ={60}^{\circ }$, $BAD\sphericalangle ={30}^{\circ }$ (lásd a 3. ábrát). A gyalogosnak tehát az $AB$-vel ${30}^{\circ }$-os szöget bezáró $AD$ szakaszon kell haladnia a $BC$ országút felé. 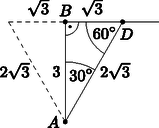  3. ábra     Gyalogosok frontja. Tüzetesebben szemügyre véve az imént kirajzolódott speciális szögeket, egy különös összefüggést fedezhetünk fel. Képzeljük el, hogy egyszerre többen szeretnének a hómezőről a leghamarabb eljutni a $C$ pontba, mégpedig a következőképpen. Az $AD$ szakaszra az $A$ pontban merőleges egyenesen az $A$ (piciny) környezetében egymás mellé felsorakoztatjuk a gyalogosokat, akik ugyanabban az időpontban indulnak el az $AD$ szakasszal párhuzamosan $v$ sebességgel az országút felé (a 4. ábrán az $A\text{'}$ és $A\text{'}\text{'}$ pontokból induló gyalogosok pályája látható). Az országút elérésekor a gyalogosok $2v$ sebességgel a $C$ pont felé haladnak tovább (egymás mellett, ha esetleg találkoznak). Azt állítjuk, hogy ekkor az összes gyalogos egyszerre érkezik a $C$ pontba (pontosabban, az országútra $C$-ben merőleges egyenesre). 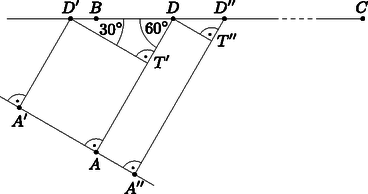  4. ábra   Vizsgáljuk például az $A$ és $A\text{'}$ pontból induló két gyalogost. A derékszögek miatt $AT\text{'}D\text{'}A\text{'}$ téglalap, ezért $AT\text{'}=A\text{'}D\text{'}$, így mikor az $A\text{'}$ pontból induló gyalogos $D\text{'}$-be ér, az $A$-ból induló a $T\text{'}$ pontba jut. Másrészt a $DD\text{'}T\text{'}$ háromszög egy szabályos háromszög fele, így $D\text{'}D=2T\text{'}D$, emiatt a $D\text{'}$-ből $2v$ sebességgel továbbhaladó gyalogos ugyanakkor ér $D$-be, mint amikor a $T\text{'}$-ből $v$ sebességgel $D$ felé haladó másik gyalogos. Az $A$ és $A\text{'}$ pontból induló két gyalogos tehát egyszerre ér $D$-be, és innen már együtt, egymás mellett mennek tovább $C$ felé. Hasonlóan látható, hogy az $A$ és $A\text{'}\text{'}$ pontokból induló gyalogosok $D\text{'}\text{'}$-be egyszerre érnek, és mennek innen tovább. Fizikai nyelven az $A$-ból induló gyalogosra tekinthetünk úgy, mint a fényre, amelyről most a Pierre de Fermat (1601‐1665) francia jogász és ,,műkedvelő'' matematikustól származó elv szerint azt feltételezzük, hogy a legrövidebb idő alatt jut el a $C$ pontba. Mint tudjuk, a fény hullámként is viselkedik, ezért egyetlen gyalogos helyett egy egész sereg gyalogosból álló, a haladás irányára merőleges front terjedésére gondolhatunk, amelyben minden gyalogos ugyanakkor érkezik a $C$ pontba. E fizikai szemléletből kiindulva a 4. ábra segítségével visszafelé okoskodva könnyedén megkapjuk, hogy a gyalogosok pályájának az országúttal ${60}^{\circ }$-os szöget kell bezárnia. Mindez természetesen nem teljes értékű megoldás, de legalábbis a végeredménynek egy igen érzékletes megsejtése.   4.1. történeti megjegyzés. Az előbbi gondolatmenet általánosítása valójában már több évszázaddal ezelőtt megfogalmazódott a holland matematikus, fizikus és csillagász, Christiaan Huygens (1629‐1695) fejében, aki egyébként különféle órák tervezésében is élen járt (az életéről a [2] könyvben olvashatunk). Az 1690-ben megjelent Traité de la lumiŠre (Értekezés a fényről) című munkájában adta közre a fény hullámtermészetéről szóló elméletét, és ‐ a 4. ábrához hasonló rajzon ‐ megmutatta (lásd [4, 33. oldal]), hogy mindebből levezethető a fénytörés Willebrord van Roijen Snellius (1580‐1626) holland csillagász és matematikus, valamint René Descartes (1596‐1650) francia filozófus és természettudós által korábban már megfogalmazott törvénye, amely szerint a beesési szög szinuszának és a törési szög szinuszának hányadosa egyenlő az egyes közegekben mért terjedési sebességek hányadosával.   5. Megoldások potyognak az égből Mielőtt a következő nevezetes egyenlőtlenségre térnénk rá, ebben a részben két további megoldást mutatunk, amelyekben felhasználjuk, hogy már megsejtettük a minimumhelyet. Az ilyesmi nem ritka a matematikában: egy fizikai érvelés vagy egy mélyebb elmélet (például differenciálszámítás) segít megsejteni a végeredményt, majd ezáltal lelünk más megoldási utakra.   Egy kis trigonometria. Az időben legrövidebb út igen speciális helyzete arra ösztönözhet, hogy megnézzük, miként fest a teljes út megtételéhez szükséges idő, ha azt például $\alpha =BAD\sphericalangle$ függvényében írjuk fel (lásd 5. ábra). Ekkor a $BAD$ háromszögben $\text{cos}\alpha =AB/AD$ és $\text{tg}\alpha =BD/AB$, így $\begin{array}{c}{\displaystyle \frac{AD}{v}+\frac{DC}{2v}=\frac{AD}{v}+\frac{BC-BD}{2v}=\frac{AB}{2v}\left(\frac{2}{\text{cos}\alpha }-\text{tg}\alpha \right)+\frac{BC}{2v}\mathrm{,}}\end{array}$ (5.1) ahol $AB=3$ és $BC=10$ adottak. A jobb oldalon a zárójelben lévő kifejezés minimumának megkeresése most sem tűnik magától értetődőnek, ám egyéb ötlet híján a differenciálszámítás elsöprő ereje bizonyára megteszi a dolgát. Ha viszont valahonnan ‐ például az előző megoldásokból ‐ már megsejtettük az $\alpha ={30}^{\circ }$ minimumhelyet, akkor elegendő a $\begin{array}{c}{\displaystyle \frac{2}{\text{cos}\alpha }-\text{tg}\alpha \ge \frac{2}{\text{cos}{30}^{\circ }}-\text{tg}{30}^{\circ }=\sqrt[]{3}}\end{array}$ egyenlőtlenséget igazolni $0\le \alpha \le BAC\sphericalangle$ esetén, ami $\text{cos}\alpha >0$ miatt egyenértékű azzal, hogy $\begin{array}{c}{\displaystyle 1\ge \frac{\sqrt[]{3}}{2}\text{cos}\alpha +\frac{1}{2}\text{sin}\alpha \mathrm{.}}\end{array}$ Mivel $\text{cos}{30}^{\circ }=\sqrt[]{3}/2$ és $\text{sin}{30}^{\circ }=1/2$, ezért az iménti egyenlőtlenség a $\begin{array}{c}{\displaystyle \text{cos}\left(\alpha -\beta \right)=\text{cos}\alpha \text{cos}\beta +\text{sin}\alpha \text{sin}\beta }\end{array}$ addíciós formula felhasználásával az $\begin{array}{c}{\displaystyle 1\ge \text{cos}\left(\alpha -{30}^{\circ }\right)}\end{array}$ nyilvánvaló alakot ölti, amelyről az egyenlőség feltétele, $\alpha ={30}^{\circ }$ is azonnal leolvasható. Ez megfelel a feladat kívánalmainak, hiszen ekkor $AB=3$ és $BC=10$ miatt $BD=\sqrt[]{3}<BC=10$. Mindez a szélsőérték-feladatunknak egy újabb, trigonometrikus megoldási módja. 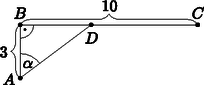  5. ábra   Vegyük észre, hogy az előbbi érvelésnek valójában az is folyománya, hogy az (5.1) kifejezés minimumhelye a $0\le \alpha \le BAC\sphericalangle$ szögtartományon $\alpha ={30}^{\circ }$ minden olyan esetben, amikor $BAC\sphericalangle \ge {30}^{\circ }$ (az $AB$ és $BC$ szakaszok konkrét hosszától függetlenül). Természetesen mindez a 2. szakaszbeli érvelésből szintén következik, ugyanis az egységek átskálázásával feltehető, hogy $AB=3$, így az (1.2) képlet csupán annyiban módosul, hogy $\begin{array}{c}{\displaystyle \frac{AD}{v}+\frac{DC}{2v}=\frac{1}{v}\left(\sqrt[]{x^2+9}+\frac{BC-x}{2}\right)=\frac{1}{v}f\left(x\right)+\frac{BC-10}{2v}\mathrm{,}}\end{array}$ ahol $0\le x\le BC$. Szóról szóra megismételve a korábbi okoskodást a minimumhelyre $x=\sqrt[]{3}$ adódik, feltéve, hogy $BC\ge \sqrt[]{3}$. Felmerül a kérdés, hogy vajon $BC<\sqrt[]{3}$ esetén a $BC$ szakasz mely pontja szolgáltatja az időben legrövidebb utat? Ebben az esetben $BD=\sqrt[]{3}$ már nem jöhet szóba, hiszen $D$ a $BC$ szakaszon kívülre esne. Ekkor például az $f$ függvény monotonitási tulajdonságai lehetnek segítségünkre.   Monotonitás elemien. Valamely ismert matematikai program segítségével kirajzolva az $f$ függvény grafikonját (6. ábra) rögtön megsejthetjük, hogy a minimumhelytől balra $f$ szigorúan monoton csökkenő, jobbra pedig szigorúan monoton növő. (Vigyázzunk, hogy egy függvény egy minimumhelytől balra és jobbra is végtelen sokszor fel-le ingadozhat ‐ oszcillálhat ‐, tehát általában nem feltétlenül kell monotonnak lennie!) Ebből következően, ha $BC<\sqrt[]{3}$, akkor az időben legrövidebb út maga a $BC$ szakasz. A monotonitási tulajdonságokat differenciálszámítás segítségével természetesen könnyedén igazolhatjuk (az áprilisi KöMaL negyedik megoldásának mintájára), de elemien sem nehéz belátni, nézzük is meg. Legyen például $x_1<x_2\le \sqrt[]{3}$, ekkor $f\left(x_1\right)>f\left(x_2\right)$ azt jelenti, hogy $\begin{array}{c}{\displaystyle \sqrt[]{x_1^2+9}+\frac{10-x_1}{2}>\sqrt[]{x_2^2+9}+\frac{10-x_2}{2}\mathrm{,}}\end{array}$ átrendezve pedig $\begin{array}{c}{\displaystyle x_2-x_1>2\left(\sqrt[]{x_2^2+9}-\sqrt[]{x_1^2+9}\right)\mathrm{.}}\end{array}$ Mindkét oldalt a pozitív $\sqrt[]{x_2^2+9}+\sqrt[]{x_1^2+9}$ kifejezéssel szorozva, valamint az $\left(a-b\right)\left(a+b\right)=a^2-b^2$ azonosságot felhasználva $\begin{array}{c}{\displaystyle \left(x_2-x_1\right)\left(\sqrt[]{x_2^2+9}+\sqrt[]{x_1^2+9}\right)>2\left(\left(x_2^2+9\right)-\left(x_1^2+9\right)\right)}\end{array}$ adódik, ahol a jobb oldal $2\left(x_2-x_1\right)\left(x_2+x_1\right)$ szorzat alakba írható át. Mivel $x_2>x_1$, így az $\left(x_2-x_1\right)$ pozitív tényezővel való ekvivalens leosztás után a $\begin{array}{c}{\displaystyle \sqrt[]{x_2^2+9}+\sqrt[]{x_1^2+9}>2\left(x_2+x_1\right)\mathrm{,}}\end{array}$ a bizonyítandó $f\left(x_1\right)>f\left(x_2\right)$ összefüggéssel egyenértékű egyenlőtlenséghez jutunk. Ez viszont $x_2\le \sqrt[]{3}$ és $x_1<\sqrt[]{3}$ miatt teljesül, hiszen ekkor $\begin{array}{c}{\displaystyle \sqrt[]{x_2^2+9}+\sqrt[]{x_1^2+9}>2\sqrt[]{12}=2\left(\sqrt[]{3}+\sqrt[]{3}\right)>2\left(x_2+x_1\right)\mathrm{.}}\end{array}$ Ezzel differenciálszámítás nélkül beláttuk $f$ szigorú monoton csökkenését $x\le \sqrt[]{3}$ esetén; az $x\ge \sqrt[]{3}$ esetén való szigorú növekedés hasonlóan igazolható (és a fentiek mintájára érdemes megpróbálkozni az (5.1) függvény monotonitási szakaszainak vizsgálatával). Ez a hómezős feladatnak ismét egy megoldása. 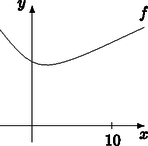  6. ábra     6. Cauchy, Bunyakovszkij és Schwarz Ebben a részben az (1.3) hozzárendeléssel értelmezett $f$ függvényben szereplő négyzetgyök kiküszöbölésének egy újabb módját mutatjuk be, amelynek ötlete a [3] cikkből származik. Fő eszközünk a következő csinos algebrai egyenlőtlenség.   6.1. állítás (Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség). Tetszőleges $a$, $b$, $c$, $d$ valós számokra $\begin{array}{c}{\displaystyle |ac+bd|\le \sqrt[]{a^2+b^2}\cdot \sqrt[]{c^2+d^2}\mathrm{.}}\end{array}$ (6.1) Egyenlőség pontosan akkor teljesül, ha $ad=bc$.   6.2. megjegyzés. Bármely $x$ valós számra $x\le |x|$ (és egyenlőség csakis $x\ge 0$ esetén van), ezért a (6.1) egyenlőtlenség igaz marad a bal oldalon szereplő abszolút érték elhagyásával. Ekkor az egyenlőség feltétele szigorúbb, $ad=bc$ mellett $ac+bd\ge 0$ is szükséges (amit sokkal elegánsabban meg lehet fogalmazni, erről nemsokára szót ejtünk a bizonyítást követő 6.5. észrevételben).   Bizonyítás. Az egyenlőtlenség mindkét oldala nemnegatív, ezért a négyzetre emelés ekvivalens átalakítás, elég tehát igazolni, hogy $\begin{array}{c}{\displaystyle {\left(ac+bd\right)}^2\le \left(a^2+b^2\right)\left(c^2+d^2\right)\mathrm{.}}\end{array}$ Innen a műveletek elvégzése után $\begin{array}{c}{\displaystyle a^2{c}^2+2acbd+b^2{d}^2\le a^2{c}^2+a^2{d}^2+b^2{c}^2+b^2{d}^2}\end{array}$ adódik, ami rendezve a $\begin{array}{c}{\displaystyle 0\le a^2{d}^2-2acbd+b^2{c}^2}\end{array}$ alakot ölti, azaz $\begin{array}{c}{\displaystyle 0\le {\left(ad-bc\right)}^2\mathrm{.}}\end{array}$ Ez nyilvánvalóan teljesül, az egyenlőség feltétele, $ad=bc$ pedig világosan leolvasható. Mivel ekvivalens átalakításokat végeztünk, sőt minden lépésben az egyenlőség esete megőrződött, ezért az eredeti egyenlőtlenség is igaz és abban ugyanakkor áll fenn egyenlőség.  $\square$   6.3. megjegyzés. Az egyenlőtlenség egy másik hagyományos bizonyítása, hogy felírjuk a nemnegatív és $a^2+b^2\ne 0$ esetén másodfokú $\begin{array}{c}{\displaystyle {\left(ax-c\right)}^2+{\left(bx-d\right)}^2=\left(a^2+b^2\right)x^2-2\left(ac+bd\right)x+c^2+d^2}\end{array}$ kifejezés diszkriminánsát, amely szükségképpen nempozitív. Ezt az Olvasóra bízzuk, az egyenlőség esetének vizsgálatával együtt.   6.4. történeti megjegyzés. A (6.1) egyenlőtlenség (abszolút érték nélküli változatának) valós szám $n$-esekre vonatkozó általánosítása a következő: $\begin{array}{c}{\displaystyle a_1{b}_1+a_2{b}_2+\text{...}+a_n{b}_n\le \sqrt[]{a_1^2+a_2^2+\text{...}+a_n^2}\cdot \sqrt[]{b_1^2+b_2^2+\text{...}+b_n^2}\mathrm{.}}\end{array}$ Ezt Augustin-Louis Cauchy (1789‐1857) francia matematikus ‐ a 6.3. megjegyzésben vázolt ötletet követve ‐ igazolta 1821-ben a híres École Polytechniqe műszaki egyetemen tartott analízis kurzusához írt könyvében. A mű a modern analízis kialakulásának fontos mérföldköve, amelyben Cauchy számos mai fogalom, köztük például a határérték, folytonosság alapjait fektette le (Cauchy összegyűjtött munkái 27 kötetet tesznek ki, amelyek a [7] weboldalon elektronikus formában megtalálhatók több más hasonlóan kiemelkedő matematikus összes műveivel együtt). Később, 1859-ben Viktor Jakovlevics Bunyakovszkij (1804‐1889) orosz matematikus az egyenlőtlenségnek integrálható függvényekre vonatkozó változatát írta fel: $\begin{array}{c}{\displaystyle {\left(\underset{a}{\overset{b}{\int }}g\left(x\right)h\left(x\right)dx\right)}^2\le \underset{a}{\overset{b}{\int }}{g}^2\left(x\right)dx\cdot \underset{a}{\overset{b}{\int }}{h}^2\left(x\right)dx\mathrm{.}}\end{array}$ Bunyakovszkij cikke kevéssé vált ismertté az akkori Nyugat-Európában, így nem tudván az eredményről Karl Hermann Amandus Schwarz (1843‐1921) német matematikus 1885-ben hasonló egyenlőtlenséget igazolt felszíni integrálokkal kapcsolatos munkájában. Ezek alapján szokás a (6.1) egyenlőtlenséget és általánosításait Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség néven emlegetni ‐ ám nyelvterületenként és matematikai iskolánként is roppant változatos, hogy a három névből álló halmaz nemüres részhalmazai közül melyikkel illetik az egyenlőtlenséget (a nevek sorrendjéről nem is beszélve).   A hómezős feladatra való alkalmazás előtt célszerű még egy észrevételt tennünk az egyenlőtlenség szemléletes jelentéséről. Akiket a megoldás jobban izgat, azok első olvasáskor továbbugorhatnak.   6.5. észrevétel. A ránézésre algebrainak tűnő (6.1) egyenlőtlenségnek valójában geometriai jelentés tulajdonítható. Vegyük észre ugyanis (lásd 7. ábra), hogy $\sqrt[]{a^2+b^2}$, $\sqrt[]{c^2+d^2}$ rendre az $\text{u}=\left(a\mathrm{,}b\right)$ és $\text{v}=\left(c\mathrm{,}d\right)$ síkbeli vektorok hossza (abszolút értéke), az $ac+bd$ kifejezés pedig a két vektor skaláris szorzata derékszögű koordinátarendszerbeli koordináták segítségével felírva (vektorok skaláris szorzatáról és geometriai alkalmazásairól bővebben lásd Reiman István (1927‐2012) ‐ a magyar matematikai tehetséggondozás legendás alakja, a diákolimpiai szakkör évtizedeken keresztüli vezetője ‐ kitűnő [5] könyvét). Ismert, hogy két vektor skaláris szorzata a hosszaik és a hajlásszögük koszinuszának szorzata. Ha most $\left(\text{u}\mathrm{,}\text{v}\right)$ jelöli $\text{u}$ és $\text{v}$ skaláris szorzatát, akkor a (6.1) egyenlőtlenség így írható: $\begin{array}{c}{\displaystyle |\left(\text{u}\mathrm{,}\text{v}\right)|=|\text{u}|\cdot |\text{v}|\cdot |\text{cos}\phi |\le |\text{u}|\cdot |\text{v}|\mathrm{.}}\end{array}$ (Vigyázzunk, itt kétféle abszolút érték is szerepel, számoké és vektoroké egyaránt.) Egyenlőség pontosan akkor áll fenn, ha $|\text{cos}\phi |=1$, vagyis az $\text{u}$, $\text{v}$ vektorok egyállásúak ‐ ellenőrizzük le, hogy ez egyenértékű a korábban kapott $ad=bc$ feltétellel. Az is világosan látszik, hogy a bal oldali abszolút érték nélküli $\left(\text{u}\mathrm{,}\text{v}\right)=|\text{u}|\cdot |\text{v}|$ egyenlőség feltétele $\text{cos}\phi =1$, tehát $\text{u}$ és $\text{v}$ azonos irányúak. Ebben a formában sokkal szemléletesebb (és könnyebben megjegyezhető) a (6.1) egyenlőtlenség, vigyázzunk azonban, hogy bár a bizonyítás ránézésre pofon egyszerű, de el van benne rejtve a skaláris szorzat koordinátákkal felírt alakja. 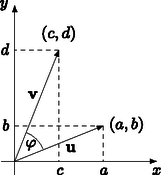  7. ábra   Figyelemre méltó még az előbbieken kívül, hogy a (6.1) egyenlőtlenségnek következménye a síkvektorokra vonatkozó háromszög-egyenlőtlenség: $\begin{array}{c}{\displaystyle |\text{u}+\text{v}|\le |\text{u}|+|\text{v}|\mathrm{.}}\end{array}$ Ez persze geometriailag világos, hiszen az $\text{u}$, $\text{v}$, $\text{u}+\text{v}$ vektorok alkotta háromszög bármely két oldalhosszának összege legalább akkora, mint a harmadik oldal hossza (lásd 8. ábra). A néha becsapós szemléletet viszont könnyedén kikerülhetjük, ugyanis koordinátákkal kifejezve arról van szó, hogy $\begin{array}{c}{\displaystyle \sqrt[]{{\left(a+c\right)}^2+{\left(b+d\right)}^2}\le \sqrt[]{a^2+b^2}+\sqrt[]{c^2+d^2}\mathrm{,}}\end{array}$ (6.2) ami ‐ négyzetre emeléssel és rendezéssel láthatóan ‐ a (6.1) egyenlőtlenség abszolút érték nélküli változatával ekvivalens. 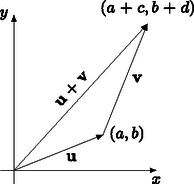  8. ábra     A hómezős feladat megoldása. Kanyarodjunk most vissza az (1.3) függvény minimumának megkereséséhez. A $\sqrt[]{x^2+9}$ kifejezés éppen az $\left(x\mathrm{,3}\right)$ vektor hossza, ami azt sugallhatja számunkra, hogy a Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenséggel próbálkozzunk. Az alkalmazásához azonban szükségünk lenne még egy vektorra, ám szerencsére ott van, csak ,,elrejtőzött'': $\begin{array}{c}{\displaystyle \sqrt[]{x^2+9}=\sqrt[]{x^2+9}\cdot 1=\sqrt[]{x^2+9}\cdot \sqrt[]{\text{cos}{}^2\beta +\text{sin}{}^2\beta }\mathrm{.}}\end{array}$ (6.3) (Amennyiben nem szeretnénk trigonometrikus függvényekkel dolgozni, akkor $\left(\text{cos}\beta \mathrm{,}\text{sin}\beta \right)$ helyett gondoljunk egyszerűen egy $\left(v_1\mathrm{,}{v}_2\right)$ egység hosszú vektorra, azaz $v_1^2+v_2^2=1$.) A $\beta$ szög számunkra megfelelő értékét egyelőre nem tudjuk, de tüstént ki fog derülni. Alkalmazzuk most a Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség abszolút érték nélküli változatát (6.3) alapján: $\begin{array}{c}{\displaystyle \sqrt[]{x^2+9}=\sqrt[]{x^2+9}\cdot \sqrt[]{\text{cos}{}^2\beta +\text{sin}{}^2\beta }\ge x\text{cos}\beta +3\text{sin}\beta \mathrm{.}}\end{array}$ (6.4) Ezzel az $f$ függvény egy alsó becslését nyerjük: $\begin{array}{c}{\displaystyle f\left(x\right)\ge x\text{cos}\beta +3\text{sin}\beta +\frac{10-x}{2}=x\left(\text{cos}\beta -\frac{1}{2}\right)+3\text{sin}\beta +5.}\end{array}$ Immár jól látszik, hogy $\text{cos}\beta =1/2$ esetén $f$-nek $x$-től független alsó becslése adódik. Legyen tehát $\beta ={60}^{\circ }$, ekkor $\text{cos}\beta =1/2$, $\text{sin}\beta =\sqrt[]{3}/2$ miatt $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{x^2+9}+\frac{10-x}{2}\ge 3\text{sin}\beta +5=\frac{3\sqrt[]{3}}{2}+5.}\end{array}$ A 6.2. megjegyzés figyelembevételével egyenlőség csakis akkor áll fenn, ha $x\cdot \frac{\sqrt[]{3}}{2}=3\cdot \frac{1}{2}$, azaz $x=\sqrt[]{3}$ (a 6.5. észrevételben foglaltak szerint úgy is fogalmazhatunk, hogy az $\left(x\mathrm{,3}\right)$ és $\left(\frac{1}{2}\mathrm{,}\frac{\sqrt[]{3}}{2}\right)$ vektoroknak azonos állásúaknak kell lenniük). Mivel $0<\sqrt[]{3}<10$, ezzel a korábbi megoldásokhoz hasonlóan megkaptuk, hogy az $f$ függvény minimumhelye a $\left[\mathrm{0,10}\right]$ intervallumon $x=\sqrt[]{3}$.   6.6. megjegyzés. A kíváncsi Olvasó eltöprenghet azon, hogy az előbbi okoskodásban felbukkanó $\beta$ szög és maga a (6.4) egyenlőtlenség az 1. ábrán vajon hogyan jeleníthető meg ‐ ehhez érdemes használni azt, hogy egy vektornak egy adott egységvektorral képzett skaláris szorzata a vektornak az egységvektor irányára vetett előjeles vetülete (lásd [5]). Az [1] könyvecskében a Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség mellett további nevezetes egyenlőtlenségekhez kapcsolódó feladatok közül válogathatunk, ezenkívül a [6] angol nyelvű könyv igazi csemege azok számára, akik az egyenlőtlenségek művészetében szeretnének kalandozni.   Hivatkozások [1] Ábrahám Gábor, Nevezetes egyenlőtlenségek, Mozaik Oktatási Stúdió, Szeged, 1995. [2] Sz. G. Gingyikin, Történetek fizikusokról és matematikusokról, Harmadik kiadás, Typotex, Budapest, 2012. [3] M. Golomb, Elementary Proofs for the Equivalence of Fermat's Principle and Snell's Law, Amer. Math. Monthly, Vol. 71, No. 5 (May, 1964), 541‐543., http://www.jstor.org/stable/2312599. [4] Ch. Huygens, Traité de la lumiŠre, Chez Pierre van der Aa, Leiden, 1690., https://archive.org/stream/traitdelalvmie00huyg. [5] Reiman István, Geometria és határterületei, Szalay Könyvkiadó és Kereskedőház Kft., 1999. [6] J. M. Steele, The Cauchy‐Schwarz Master Class (An Introduction to the Art of Mathematical Inequalities), Cambridge Univ. Press, NY, 2004. [7] Gallica-Math, http://sites.mathdoc.fr/OEUVRES.