Kezdőlap


Cím:	Séta a havon ‐ az ezerarcú feladat 1.
Szerző(k):	Besenyei Ádám
Füzet:	2016/november, 455 - 461. oldal	PDF \| MathML
Hivatkozás(ok):	2016/december: Séta a havon ‐ az ezerarcú feladat 2. 2017/január: Séta a havon ‐ az ezerarcú feladat 3.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A változatosság gyönyörködtet ‐ tartja a mondás. Egy matematikai probléma szépségét például gyakorta a megoldáshoz vezető utak sokszínűsége és egymásba fonódása adja. A különféle nézőpontok szerepet játszhatnak a mélyebb megértésben és egymástól távolinak tűnő területek összekapcsolásában, amint ennek a KöMaL hasábjain sűrűn szemtanúi lehetünk. Írásunkban is éppen a megoldások roppant gazdagságának érzékeltetését tűzzük ki célul, méghozzá a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium matematika munkaközössége által összeállított és a 2016. márciusi számban megjelent, az emelt szintű matematika érettségire való gyakorlást szolgáló feladatsor egy szélsőérték-feladata kapcsán.

Feladat. Egy gyalogos a hóval borított mező

A

pontjában van,

3

kilométernyire a

B C

egyenes úttól (az 1. ábrán

A B = 3

km,

B C = 10

km). Az országúton a gyalogos kétszer akkora sebességgel halad, mint a hómezőn. Mely

D

pontban kell kimennie a gyalogosnak az útra, hogy a legrövidebb idő alatt jusson el

C

-be?

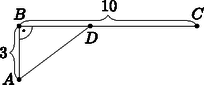1. ábra

Az áprilisi számban a kitűzők igazán tetszetős módon négy különböző megoldását mutatták be az iménti feladatnak: egy algebrai, egy függvénytani és egy elemi geometriai utat, valamint az optika Snellius‐Descartes-féle fénytörési törvényén alapuló fizikai szemléletű megközelítést. Célunk, hogy mindezt megtoldjuk további megoldásokkal, segítségül hívva nevezetes egyenlőtlenségeket és a mechanikát. Felbukkan a számtani és mértani közép közötti egyenlőtlenség, a Cauchy‐Bunyakovszkij‐Schwarz-egyenlőtlenség, valamint a húrnégyszögek Ptolemaiosz-egyenlőtlensége. Szó esik ezenkívül még az Euler-féle helyettesítésekről, négyzetszámok táblázatairól, hullámfrontokról, erők eredőjéről és mindemellett a matematikatörténeti érdekességek sem maradnak el. Közben pedig számos töprengési lehetőséget és bőséges olvasnivalót kínálunk az érdeklődő Olvasó számára. Javasoljuk, hogy a továbbhaladás előtt próbálkozzon meg minél többféle megoldás önálló kigondolásával, majd ezután az áprilisi szám megfelelő oldalaira ugyancsak érdemes visszalapoznia. A megoldások színes és szerteágazó sokaságán keresztül remélhetőleg feltárulnak a feladat rejtett kincsei és alkalom nyílik a gyönyörködésre.

1. Kezdeti lépések a havon

Jóllehet a feladat szövege és az 1. ábra is azt sugallja, hogy a

D

pontnak a

B C

szakaszon kell lennie, mindenesetre nem árt meggondolnunk, hogy az időben legrövidebb út szempontjából a

B C

egyenes többi pontját kizárhatjuk. Valóban, ha a 2. ábrán látható módon a

D_{1}

pont a

B C

egyenesen

B

-től balra van, akkor nyilván

B C < D_{1} C

, továbbá az

A B D_{1}

derékszögű háromszögben

A D_{1}

átfogó, ezért

A B < A D_{1}

. Következésképpen az

A B C

töröttvonal mindkét szakasza rövidebb az

A D_{1} C

töröttvonal megfelelő szakaszainál, így a megtételükhöz is kevesebb idő kell, tehát van az

A D_{1} C

töröttvonalnál időben rövidebb út. Amennyiben egy, a

C

-től jobbra eső

D_{2}

pontot tekintünk, akkor

D_{2} C A ∢

tompaszög (miért?), emiatt a

D_{2} C A

háromszögben

A D_{2}

a leghosszabb oldal, így már önmagában az

A D_{2}

út megtétele több időbe telik, mint egyszerűen az

A C

szakaszon végigmenni.

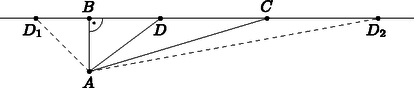2. ábra

Ezek után legyen a gyalogos sebessége a hómezőn

v

, az országúton pedig

2 v

(ahol

v > 0

), ekkor az

A D C

töröttvonal út megtételéhez szükséges idő:

\begin{matrix} \frac{A D}{v} + \frac{D C}{2 v} = \frac{1}{v} (A D + \frac{D C}{2}) . \end{matrix}

(1.1)

Világos, hogy a minimum helyének szempontjából

v

nem játszik szerepet, ezért elég csupán a zárójelben lévő kifejezést vizsgálni (más szóval feltehető

v = 1

), amelyet írjunk fel a

D

pont

B

-től (km-ben) mért távolságának függvényében a KöMaL áprilisi számában közölt első megoldáshoz hasonlóan.
Ha

B D = x

, ahol

0 \leq x \leq 10

, akkor

D C = 10 - x

, továbbá az

A D B

derékszögű háromszögben a Pitagorasz-tétel alapján

A D = \sqrt[]{x^{2} + 9}

, így

\begin{matrix} A D + \frac{D C}{2} = \sqrt[]{x^{2} + 9} + \frac{10 - x}{2} . \end{matrix}

(1.2)

Elegendő tehát az

\begin{matrix} f (x) : = \sqrt[]{x^{2} + 9} + \frac{10 - x}{2} \end{matrix}

(1.3)

függvény minimumának helyét megkeresni

0 \leq x \leq 10

esetén. Az áprilisi szám 204‐206. oldalain erre két okoskodást olvashattunk: az egyik egy másodfokú paraméteres egyenlet diszkriminánsának vizsgálatára vezeti vissza a kérdést, a másik pedig differenciálszámítás segítségével adja meg a szélsőértékhelyet. Most az (1.3) hozzárendelési szabályban szereplő négyzetgyök kiküszöbölésére először egy rafinált helyettesítést mutatunk.

2. Egy ravasz gondolat

A szakasz gondolatmenete a ,,hómezős'' feladattal együtt megtalálható Hódi Endre (1923‐2003) ‐ aki sok éven át a matematikai diákolimpiai csapat kísérője és a tehetséggondozás aktív szereplője volt ‐ szélsőérték-feladatok elemi megoldásáról szóló remek könyvecskéjében (lásd [2, 109‐112. feladat]). A megoldásnak erre az ötletére e sorok írójának figyelmét Németh József, a szegedi Bolyai Intézet kitűnő oktatója hívta fel, aki a mindennapi életben előforduló szélsőérték-problémákról tartott előadásában a hómezős feladat olajvezeték építési költségének minimalizálására átfogalmazott változatát (lásd [5, 8. feladat]) oldotta meg az egykori mesterétől, ‐ a nemzetközileg kiemelkedő matematikus és tanáregyéniség ‐ Kalmár Lászlótól (1905‐1976) tanult elemi módszerrel. Lássuk az ötletet!
Célunk, hogy az (1.3) kifejezésben szereplő négyzetgyök használatát egy ügyes helyettesítéssel elkerüljük. Ehhez induljunk ki a jól ismert

\begin{matrix} {(u + v)}^{2} - {(u - v)}^{2} = 4 u v \end{matrix}

(2.1)

algebrai azonosságból. Ha most

v = \frac{1}{4 u}

, akkor ebből átrendezés után

\begin{matrix} {(u - \frac{1}{4 u})}^{2} + 1 = {(u + \frac{1}{4 u})}^{2} \end{matrix}

adódik. Még praktikusabb, ha az iménti összefüggés

9

-szeresét tekintjük:

\begin{matrix} {[3 (u - \frac{1}{4 u})]}^{2} + 9 = {[3 (u + \frac{1}{4 u})]}^{2}, \end{matrix}

(2.2)

hiszen ez nyomban az

x = 3 (u - \frac{1}{4 u})

vagy

x = - 3 (u - \frac{1}{4 u})

helyettesítést sugallja. Ekkor ugyanis

u > 0

feltételezésével (2.2) alapján

\begin{matrix} \sqrt[]{x^{2} + 9} = 3 (u + \frac{1}{4 u}) . \end{matrix}

(2.3)

Ha például az

\begin{matrix} x = 3 (u - \frac{1}{4 u}) \end{matrix}

(2.4)

helyettesítést választjuk, akkor

\begin{matrix} \sqrt[]{x^{2} + 9} + \frac{10 - x}{2} = 3 (\frac{u}{2} + \frac{3}{8 u}) + 5. \end{matrix}

(2.5)

Ezáltal a minimalizálandó kifejezésünk egy csapásra olyan alakot öltött, amely tálcán kínálja a számtani és mértani közép közötti egyenlőtlenség alkalmazását: tetszőleges

u

pozitív számra

\begin{matrix} 3 (\frac{u}{2} + \frac{3}{8 u}) + 5 \geq 3 \cdot 2 \cdot \sqrt[]{\frac{u}{2} \cdot \frac{3}{8 u}} + 5 = \frac{3 \sqrt[]{3}}{2} + 5. \end{matrix}

(2.6)

Egyenlőség pontosan akkor áll fenn, ha

u / 2 = 3 / (8 u)

, ahonnan

u > 0

folytán

u = \sqrt[]{3} / 2

következik, és ekkor a (2.4) helyettesítés értelmében

x = \sqrt[]{3}

. Mivel ez megfelel a

0 \leq x \leq 10

kívánalomnak, így a (2.5) és (2.6) összefüggések figyelembevételével azt kapjuk, hogy az

f

függvény a

[0,10]

intervallumon a minimumát az

x = \sqrt[]{3}

pontban veszi fel (és a minimum értéke

3 \sqrt[]{3} / 2 + 5

).
Álljunk csak itt meg egy pillanatra, biztosan nem felejtettünk el semmit az előbbi gondolatmenetben? Hogyan is okoskodtunk? Meghatároztuk a (2.5) azonosság jobb oldalának minimumhelyét a pozitív

u

számok halmazán és ebből a bal oldali kifejezés

0 \leq x \leq 10

esetén vett minimumának helyére következtettünk. De milyen

x

értékekre érvényes egyáltalán a szóban forgó (2.5) azonosság? Olyan

x

valós számokra, amelyek előállnak (2.4) alakban valamilyen

u > 0

esetén. Vajon előáll minden

x \in [0,10]

szám ilyen módon? Nem fordulhat elő, hogy ,,bizonyos''

x \in [0,10]

számok esetleg nem írhatók fel (2.4) alakban és ráadásul ezekre az

x

-ekre

f

kisebb értéket vesz fel, mint a

\sqrt[]{3}

pontban? Szerencsére a (2.4) összefüggés

u

-ra nézve valójában egy másodfokú egyenletre vezet, így gond nélkül megoldhatjuk:

\begin{matrix} u_{1} = \frac{1}{6} (x + \sqrt[]{x^{2} + 9}) és u_{2} = \frac{1}{6} (x - \sqrt[]{x^{2} + 9}) . \end{matrix}

Minthogy tetszőleges

x \in R

esetén

\sqrt[]{x^{2} + 9} > \sqrt[]{x^{2}} = | x | = {max}_{}^{} {x, - x}

(egy

x

szám abszolút értéke

x

és

(- x)

közül a nemnegatív, vagyis a nem kisebbik), ezért

u_{1} > 0

u_{2} < 0

. Ez azt jelenti, hogy bármely

x

valós számhoz egyértelműen létezik olyan

u

pozitív szám (és ezenfelül egy negatív is), amellyel

x

előáll (2.4) alakban, mégpedig

\begin{matrix} u = \frac{1}{6} (x + \sqrt[]{x^{2} + 9}), \end{matrix}

(2.7)

következésképpen a (2.4) helyettesítés egy kölcsönösen egyértelmű megfeleltetést ‐ más szóval bijekciót ‐ ad meg a valós és a pozitív valós számok halmaza között (és emellett a valós és a negatív valós számok között is). A szemfülesebbek minderre természetesen a (2.3) és (2.4) összefüggések tükrében egyenletmegoldás nélkül is következtethetnek, az analízisben jártasak pedig akár elvégezhetik az

u \mapsto u - \frac{1}{4 u}

függvény teljes vizsgálatát.
Összefoglalva, a (2.5) azonosság érvényes minden

0 \leq x \leq 10

esetén valamely

u > 0

számmal, ezért csakugyan helyesen következtettünk a bal oldal minimumának helyére a jobb oldal pozitív számokon vett minimumhelyéből, így az

f

függvény a

[0,10]

intervallumon a legkisebb értékét az

x = \sqrt[]{3}

pontban veszi fel. A gyalogosnak tehát a

B

-től

\sqrt[]{3}

km-re lévő

D

pontban kell kimennie az országútra, hogy a legrövidebb idő alatt érjen a

C

pontba.

2.1. megjegyzés. Ha (2.4) helyett

x = - 3 (u - \frac{1}{4 u})

, akkor

u > 0

folytán

\begin{matrix} u = \frac{1}{6} (\sqrt[]{x^{2} + 9} - x), \end{matrix}

(2.8)

és ennek segítségével az előzőekhez hasonlóan vizsgálhatjuk az

f

függvényt. Sőt, a (2.1) azonosságban

v = \frac{1}{4 u}

helyett választhatunk más

u

v

párokat, a lényeg csupán, hogy a

4 u v = 1

összefüggés fennálljon ‐ a különféle esetek mélyrehatóbb vizsgálatát az Olvasóra bízzuk.
A (2.7) vagy (2.8) helyettesítésekre rábukkanhatunk úgy is, ha a számtani és mértani közép közötti egyenlőtlenség lebeg a szemünk előtt. A megfelelő alsó becslés érdekében ekkor olyan mennyiségeket célszerű felfedeznünk az

f

függvény (1.3) alakjában, amelyek szorzata állandó. És lám:

\begin{matrix} (\sqrt[]{x^{2} + 9} + x) \cdot (\sqrt[]{x^{2} + 9} - x) = {(\sqrt[]{x^{2} + 9})}^{2} - x^{2} = 9. \end{matrix}

Mindezek a helyettesítések valójában már nagyon régen felbukkantak a matematikában, erről a következő szakaszban mesélünk.

3. Pihenő: négyzettáblázatok, Euler-helyettesítések

Ebben a részben egy csöppet még elidőzünk a (2.1) azonosság, valamint a (2.7), (2.8) helyettesítésekkel kapcsolatban felmerülő érdekességek és történeti háttér mentén. Mindez nem feltétlenül tartozik szorosan a megoldások folyamába, ezért első olvasásra nyugodtan a következő szakaszra lehet ugrani.

Szorzás és négyzetre emelés. Kezdjük először a (2.1) azonossággal, amelyet úgy is írhatunk, hogy

\begin{matrix} {(\frac{u + v}{2})}^{2} - {(\frac{u - v}{2})}^{2} = u v . \end{matrix}

(3.1)

Ez azt fejezi ki, hogy két szám szorzatának kiszámítása megfelelő értelemben visszavezethető négyzetre emelésekre. Első ránézésre a formula összetettnek tűnik, ám nagy számok esetén hatékonyabb módszert adhat a szorzás közvetlen elvégzésénél. Ezt a 19. század elejétől kezdve többen felismerték és készítettek az egész számok négyzeteihez kapcsolódó táblázatokat. Jakob Philipp Kulik (1793‐1863) osztrák matematikus 1851-ben például az 1-től 29 999-ig terjedő egész számok négyzeteinek

1 / 4

-szeresét foglalta táblázatba. Erről bővebben olvashatunk a [6] cikkben, ezenkívül a [7] weboldalon számos, az 1500-as évektől kezdődően készült, a kézi számolást segítő táblázatot tanulmányozhatunk. Természetesen a modern számítógépek elterjedésével ezek a táblázatok ‐ ahogyan a középiskolai négyjegyű függvénytáblázat különböző számtáblázatai ‐ fokozatosan jelentőségüket vesztették.
A szorzás négyzetre emelésre való visszavezetése nemcsak a konkrét számolásokat teheti könnyebbé, hanem elméleti okoskodásokban szintén hasznunkra válhat. Ha összeadás, kivonás, számmal való szorzás, valamint négyzetre emelés során megőrződik valamely tulajdonság ‐ ezt sok esetben könnyű igazolni ‐, akkor ezt a tulajdonságot általában a szorzás ugyancsak megtartja. Ily módon is igazolható például, hogy két konvergens sorozat szorzatának határértéke a két sorozat határértékének szorzata, vagy bizonyítható a differenciálható függvények szorzatának deriválására vonatkozó Leibniz-formula, vagy éppen két Riemann-integrálható függvény szorzatának integrálhatósága ‐ többek között Kalmár László szintén így szerette tanítani, lásd a [3] tankönyvének megfelelő részeit. Illusztrációképpen álljon itt a szorzat deriválási szabályának a (2.1) azonosságra támaszkodó szellemes bizonyítása: ha már tudjuk, hogy tetszőleges

f, g : R \to R

differenciálható függvényekre és

λ

valós számra

(f + g)' = f' + g'

(λ f)' = λ f'

, valamint

(f^{2})' = 2 f f'

, akkor

\begin{matrix} (f g)' & = ({(\frac{f + g}{2})}^{2} - {(\frac{f - g}{2})}^{2})' = \\ = 2 \cdot \frac{f + g}{2} \cdot \frac{f' + g'}{2} - 2 \cdot \frac{f - g}{2} \cdot \frac{f' - g'}{2} = f' g + f g' . \end{matrix}

Megemlítjük, hogy Gottfried Wilhelm Leibniz (1646‐1716) német filozófus és matematikus ‐ a differenciál- és integrálszámítás felfedezője Newton mellett ‐ 1675. november 11-ei kéziratában még tévesen úgy vélte, hogy szorzat deriváltja a tényezők deriváltjainak szorzata, ám tíz napra rá már tudta a helyes összefüggést (Leibnizről bővebben lásd az [1] könyv megfelelő fejezetét).

Euler és a helyettesítések. A (2.7) vagy (2.8) helyettesítésekre visszakanyarodva érdemes kiemelnünk, hogy ezeket Leonhard Euler (1707‐1783) svájci matematikus ‐ a matematikatörténet egyik legsokoldalúbb és legtermékenyebb géniusza ‐ részletesen tárgyalta 1748-ban kiadott Introductio in analysin infinitorum (Bevezetés a végtelenek analízisébe) című kétkötetes művében, amelyben összefoglalta mindazt, ami szerinte az elenyészően kis mennyiségek analíziséhez szükséges. Az első kötet 3. fejezetében Euler többek között az

y (x) = \sqrt[]{a x^{2} + b x + c}

alakú négyzetgyökös kifejezések racionális törtfüggvénnyé (azaz két polinom hányadosává) való alakításához adott meg helyettesítéseket. Ha a

p (x) = a x^{2} + b x + c

másodfokú polinom mindenhol pozitív értékű, akkor szükségképpen

a > 0

és

c = p (0) > 0

, és ekkor az

\begin{matrix} u = \sqrt[]{a x^{2} + b x + c} - \sqrt[]{a} x vagy u = \frac{\sqrt[]{a x^{2} + b x + c} - \sqrt[]{c}}{x} \end{matrix}

(3.2)

új változókat vezette be Euler, amelyekre napjainkban Euler-féle helyettesítésekként szokás hivatkozni. Valójában mindkét képletben különbség helyett összeg is vehető, és így az elsőből lényegében megkapjuk a (2.7), (2.8) helyettesítéseket. Az Olvasó számára javasoljuk annak ellenőrzését, hogy ezekkel a helyettesítésekkel

y

u

változónak valóban racionális törtfüggvényévé válik (voltaképpen mindezt végigcsináltuk a 2. szakaszban

y

helyett az

f

függvénnyel). Azon szintén érdemes eltűnődni, hogy vajon milyen helyettesítést javasolt Euler abban az esetben, amikor az

a x^{2} + b x + c

polinomnak két valós gyöke van. Ezután ugyancsak megéri Euler eredeti művébe belepillantani, amely mai szemmel is kiválóan érthető (az összes művei különféle fordításokban olvashatók a [8] weboldalon). Módszerei és meglátásai közül ‐ amint a fenti példa jól mutatja ‐ számtalan mindörökre beépült a matematikai gondolkodásba (Eulerről bővebben olvashatunk az [1] könyvben).
A (3.2) helyettesítések talán ismerősek lehetnek az integrálszámításban jártasak számára, hiszen ott gyakran van szükség négyzetgyökös, a

\sqrt[]{x^{2} + 1}

kifejezést tartalmazó integrálok kiszámítására. Persze, az

\begin{matrix} u = \sqrt[]{x^{2} + 1} - x, azaz x = \frac{u - \frac{1}{u}}{2} \end{matrix}

új változó bevezetésénél túlnyomórészt a sokkal kényelmesebb úgynevezett hiperbolikus függvényeket használjuk, vagyis

\begin{matrix} x = \frac{e^{t} - e^{- t}}{2} = sh t, \end{matrix}

ahol

sh

a szinusz hiperbolikusz függvény. A

\sqrt[]{x^{2} - 1}

alakú kifejezés pedig

\begin{matrix} x = \frac{u + \frac{1}{u}}{2} vagy x = \frac{e^{t} + e^{- t}}{2} = ch t \end{matrix}

helyettesítésekkel ,,racionalizálható'', ahol

ch

a koszinusz hiperbolikusz függvény, amelynek grafikonját láncgörbének szokás hívni, ugyanis ahhoz hasonló alakot vesz fel a két végén felfüggesztett lánc. (A szinusz és koszinusz hiperbolikusz függvényekről annyit máris tudunk, hogy

ch^{2} t - sh^{2} t = 1

, ami nem más, mint a (3.1) összefüggés egy újabb megnyilvánulási formája.) Végül pedig a

\sqrt[]{1 - x^{2}}

alakú kifejezés esetén a trigonometrikus

x = sin t

vagy

x = cos t

helyettesítés lehet a leginkább célravezető. Mindezekről (beleértve a láncgörbét) a [4] tankönyvben teljes részletességgel olvashatunk.

Hivatkozások

[1]	Sz. G. Gingyikin, Történetek fizikusokról és matematikusokról, Harmadik kiadás, Typotex, Budapest, 2012.

[2]	Hódi Endre, Szélsőérték-feladatok elemi megoldása, 3. kiadás, Typotex, Budapest, 1998.

[3]	Kalmár László, Bevezetés a matematikai analízisbe I‐II., Tankönyvkiadó, Budapest, 1982.

[4]	Laczkovich Miklós, T. Sós Vera, Valós Analízis I., TypoTeX, Budapest, 2012.

[5]	Németh József, Szélsőérték-problémák a mindennapi életben, http://www.math.u-szeged.hu/~nemethj/orosh13.pdf.

[6]	D. Roegel, A reconstruction of Kulik's table of multiplication (1851), http://locomat.loria.fr/kulik1851/kulik1851doc.pdf.

[7]	Loria Collection of Mathematical Tables, http://locomat.loria.fr.

[8]	Euler Archive, http://eulerarchive.maa.org.