Cím:	A 43. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Sarló Ferenc ,  Vankó Péter ,  Vigh Máté
Füzet:	2012/november, 489 - 501. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Elméleti feladatok   1. feladat. Ragadd meg a lényeget! A rész. Hajítás. i. Ha a golyót függőlegesen felfelé dobjuk, akkor ‐ a mechanikai energia megmaradása alapján ‐ eléri az $x=0$, $z=\frac{v_0^2}{2g}$ pontot. Ezt összehasonlítva a $z\le z_0-k{x}^2$ egyenlőtlenséggel $\begin{array}{c}{\displaystyle z_0=\frac{v_0^2}{2g}}\end{array}$ adódik. A $k$ állandó meghatározásához vizsgáljuk a $z\to -\infty$ határesetet! Ebben a határesetben a golyó akkor jut (adott $z$ érték esetén) vízszintes irányban a legmesszebbre, ha a parabolapálya a leglaposabb, azaz ha a golyót vízszintesen hajítjuk el. Ekkor $\begin{array}{c}{\displaystyle z=-\frac{g}{2v_0^2}{x}^2\mathrm{.}}\end{array}$ Ezt beírva a megadott, most $x\to \infty$ határesetben vizsgált egyenlőtlenségbe $\begin{array}{c}{\displaystyle -\frac{g}{2v_0^2}{x}^2\le z_0-k{x}^2\mathrm{,}\text{azaz}k-\frac{g}{2v_0^2}\le \frac{z_0}{x^2}\to 0.}\end{array}$ Innen $k\le \frac{g}{2v_0^2}$. Ha $k<\frac{g}{2v_0^2}$ teljesülne, akkor (nagy $x$-re) a golyó által elérhető tartomány és a megadott egyenlőtlenség által meghatározott tartomány között egy ,,rés'' lenne, ezt a lehetőséget tehát kizárhatjuk. Eszerint a kérdezett paraméter: $\begin{array}{c}{\displaystyle k=\frac{g}{2v_0^2}\mathrm{.}}\end{array}$   ii. A golyó pályája megfordítható, így az eredeti kérdés helyett vizsgálhatjuk ezt is: legalább mekkora sebességgel kell az épület tetejéről eldobni a golyót, hogy valahol földet érjen (anélkül, hogy az épületnek ütközne). Könnyen belátható, hogy a golyó pályája vagy az 1. ábrán látható, az épületet érintő parabola, vagy pedig egy olyan vízszintes hajítás, ahol a parabola görbülete a csúcspontjában megegyezik a gömb sugarával. (Ha a golyó sehol nem érinti a parabolát, akkor csökkenthető a sebessége, egész addig, amíg valahol érinteni fogja.)   1. ábra   Vizsgáljuk meg a vízszintes hajítást! Ha változatlan sebességgel, de a vízszinteshez képest kis szöggel felfelé dobnánk a golyót, akkor sehol sem érintené az épületet ‐ így viszont kezdeti sebessége csökkenthető lenne! Ebből következik, hogy a vízszintes hajítás nem lehet ideális, így a helyes megoldás az 1. ábrán látható pálya.   iii. Vegyük észre, hogy az egész épületnek benne kell lenni abban a tartományban, amit az épület tetejéről induló, minimális sebességű hajításokkal el tudnánk találni. (Hiszen ha az optimálishoz képest csökkentjük az eldobás vízszintessel bezárt szögét, akkor a golyó nem érinti, hanem eltalálja az épületet.) Ugyanakkor a dobással elérhető tartomány határának érinteni kell az épületet. (Ellenkező esetben az optimális sebességgel lehetne úgy hajítani, hogy az nem érinti az épületet.) Tehát a minimális sebességgel eldobott golyóval elérhető tartomány határa és az épület felszíne érinti egymást (a szimmetria miatt két pontban). Ha a minimális indítási sebesség a gömb tetejéről $v_0$, akkor a következő egyenletrendszert kapjuk: $\begin{array}{c}{\displaystyle x^2+z^2+2zR=\mathrm{0,}z=\frac{v_0^2}{2g}-\frac{g{x}^2}{2v_0^2}\mathrm{.}}\end{array}$ $z$ kiküszöbölésével $x^2$-re a következő másodfokú egyenlet adódik: $\begin{array}{c}{\displaystyle {\left(\frac{g}{2v_0^2}\right)}^2{x}^4+\left(\frac{1}{2}-\frac{gR}{v_0^2}\right)x^2+\left(\frac{v_0^2}{4g}+R\right)\frac{v_0^2}{g}=0.}\end{array}$ A két görbe akkor érinti egymást, amikor az egyenlet diszkriminánsa éppen 0. Ebből $\begin{array}{c}{\displaystyle {\left(\frac{1}{2}-\frac{gR}{v_0^2}\right)}^2=\frac{1}{4}+\frac{gR}{v_0^2}\mathrm{,}\text{azaz}{v}_0^2=\frac{gR}{2}\mathrm{.}}\end{array}$ A mechanikai energia megmaradása alapján a keresett minimális indítási sebesség $\begin{array}{c}{\displaystyle v_{\underset{}{\overset{}{\text{min}}}}=\sqrt[]{v_0^2+4gR}=3\sqrt[]{\frac{gR}{2}}\mathrm{.}}\end{array}$   B rész. Légáramlás a szárny körül. i. A szárnyhoz rögzített vonatkoztatási rendszerben a kontinuitási törvény miatt két áramvonal között (egy áramlási vonal mentén) állandó a levegő térfogatárama (az időegységenként átáramló levegő mennyisége). A térfogatáram a sebesség és a keresztmetszet szorzata. A keresztmetszet viszont esetünkben ‐ a kétdimenziós geometria miatt ‐ arányos az áramvonalak távolságával, ami a 2. ábráról leolvasható. Mivel nincsen szél, a nyugalomban lévő levegő sebessége a szárnyhoz viszonyítva éppen $v_0$. Az ábrán megmérve $a=10$ egység és $b=13$ egység. Ez alapján a levegő sebessége a $P$ pontban a szárnyhoz képest $u=v_0\frac{a}{b}$, a földhöz képest pedig 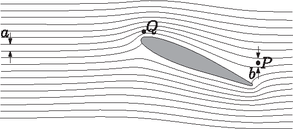$\begin{array}{c}{\displaystyle v_P=v_0-u=v_0\left(1-\frac{a}{b}\right)=23\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$   2. ábra     ii. Bár az $\frac{1}{2}\rho v^2$ dinamikus nyomás aránylag kicsi, változása bizonyos mértékű adiabatikus összenyomódást vagy kitágulást eredményez. Ott, ahol a levegő kitágul, a hőmérséklete lecsökken, és ha a hőmérséklet eléri a harmatpontot, akkor a vízgőz kicsapódik, apró vízcseppek jelennek meg. A kicsapódás ott kezdődik meg, ahol a kitágulás maximális, azaz ahol a levegő (statikus) nyomása minimális. A Bernoulli-törvény szerint $p+\frac{1}{2}\varrho v^2=$ állandó, így $p$ ott lesz a legkisebb, ahol $v$ (a levegő szárnyhoz viszonyított sebessége) a legnagyobb, azaz ahol az áramvonalak a legközelebb vannak egymáshoz. Ez a 2. ábrán $Q$-val jelölt pont.   iii. Először meg kell határoznunk a harmatpontot. A vízgőz nyomása $p_{\text{w}}=p_{\text{sa}}r=\mathrm{2,08}\text{kPa}$. A kis változások miatt a gőznyomás hőmérséklet-függését tekinthetjük közelítőleg lineárisnak: $\begin{array}{c}{\displaystyle \frac{p_{\text{sa}}-p_{\text{w}}}{T_a-T}=\frac{p_{\text{sa}}-p_{sb}}{T_a-T_b}\mathrm{,}}\end{array}$ amiből $T\approx 291\mathrm{,}5\text{K}$ adódik. Ezután meg kell határozni a levegő sebessége és hőmérséklete közti kapcsolatot. A Bernoulli-törvényhez hasonlóan egy energiamérleget írhatunk fel, de figyelembe kell vennünk a levegő összenyomásával/kitágulásával kapcsolatos munkát is. Mivel a levegő rossz hővezető, és az áramlás során gyorsak a változások, a folyamat adiabatikus. Egy áramlási cső (például két közeli áramvonal közötti térrész) két pontjára (1 és 2) felírva a munkatételt egy mol levegőre az $\begin{array}{c}{\displaystyle \frac{1}{2}M{v}_1^2+c_{V}M{T}_1+p_1{V}_1=\frac{1}{2}M{v}_2^2+c_{V}M{T}_2+p_2{V}_2}\end{array}$ összefüggést kapjuk, ahol $M$ a levegő moláris tömege, $c_V$ pedig az állandó térfogaton mért fajhő. (Az első tag a gáz mozgási energiája, a második a belső energiája, a harmadik pedig a gáz benyomásakor végzett munka.) Felhasználva, hogy egy mol gázra $pV=RT$, és $c_{V}M+R=c_{p}M$, azt kapjuk, hogy $\frac{1}{2}{v}^2+c_{p}T=$ állandó. Ebből $\begin{array}{c}{\displaystyle c_p\Delta T=-\Delta \frac{v^2}{2}=\frac{1}{2}{v}_{\text{krit.}}^2\left(1-\frac{a^2}{c^2}\right)\mathrm{,}}\end{array}$ ahol $c$ az áramvonalak távolsága a $Q$ pontban. Felhasználva, hogy $c\approx 4\mathrm{,}5$ egység és $\Delta T=-1\mathrm{,}5\text{K}$, $\begin{array}{c}{\displaystyle v_{\text{krit.}}=c\sqrt[]{\frac{2c_p\Delta T}{c^2-a^2}}\approx 23\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$   Megjegyzés: A valóságban ennél valamivel nagyobb sebesség szükséges, mert a levegő hirtelen kicsapódása csak jelentős túltelítés hatására indul meg.   C rész. Mágneses csövek. i. A cső szupravezető falán nem mehetnek át indukcióvonalak, így a csőben állandó a fluxus. A cső belsejében örvénymentes a tér, a két feltételből együtt pedig adódik, hogy homogén is, azaz az indukcióvonalak párhuzamosak, és egyenlő távolságra vannak egymástól.   Megjegyzés: A csövön kívül a tér hasonlít a vékony, hosszú tekercs (szolenoid) mágneses teréhez, azzal a fontos különbséggel, hogy a szolinoid végeinek közelében a tekercs oldalán is lépnek ki indukcióvonalak, a szupravezető csőnél ez nem lehetséges. A másik különbség: a szolenoid árama (egyenletes tekercselés esetén) hosszegységenként mindenhol ugyanakkora, a szupravezető cső falában folyó áram pedig a végek közelében nem egyenletes.   A szupravezető cső indukcióvonalait vázlatosan a 3. ábra mutatja.   3. ábra     ii. Nyújtsuk meg gondolatban egy kicsiny $\Delta \ell$ értékkel a csövet, és vizsgáljuk meg, hogy ehhez mennyi munkára van szükség! A cső fluxusa nem változhat (mert a fluxusváltozás a szupravezetőben végtelen nagy áramokat indukálna), így a mágneses indukció is állandó: $B=\frac{\Phi }{\pi r^2}$. A mágneses tér energiasűrűsége $\frac{1}{2{\mu }_0}{B}^2$, amiből a cső megnyújtásához szükséges munka $\begin{array}{c}{\displaystyle \Delta W=\frac{1}{2{\mu }_0}{B}^2\Delta V=\frac{1}{2{\mu }_0}\frac{{\Phi }^2}{{\pi }^2{r}^4}\pi r^2\Delta \ell =\frac{{\Phi }^2}{2{\mu }_0\pi r^2}\Delta \ell \mathrm{.}}\end{array}$ Ezt a munkát a húzóerő végzi: $\Delta W=T\Delta \ell$, amiből a keresett erő $\begin{array}{c}{\displaystyle T=\frac{{\Phi }^2}{2{\mu }_0\pi r^2}\mathrm{.}}\end{array}$   iii. A csövek között fellépő erő iránya ‐ az elrendezés szimmetriája miatt ‐ nyilván merőleges a csövek tengelyére. Az erő nagyságát egy elektrosztatikus analógia alapján fogjuk meghatározni. Vizsgáljuk meg, hogyan változik a rendszer mágneses energiája, ha az egyik csövet egy kicsit elmozdítjuk, eltávolítjuk a másiktól! A csövek belsejében semmi se változik, mert a csövek fluxusa állandó, csak a külső tér változik. A csöveken kívül a mágneses indukció örvénymentes (mert nincsenek áramok), a csövek végpontjai $\pm \Phi$ erősségű források, ezeken kívül viszont mindenhol forrásmentes a tér. Ezek a csöveken kívül pontosan olyan feltételek, mint amilyenek négy $\pm Q$ nagyságú elektromos töltés elektromos terét jellemzik. (A csöveken belül természetesen különböző a két tér, és a csövek falai is az elektromos esettől különböző határfelületet jelentenek, de három dimenzióban a vékony csövek elhanyagolható módon torzítják a csöveken kívüli teret.) Ezek szerint a csövek végpontjait úgy tekinthetjük, mintha mágneses ponttöltések lennének. Keressük meg az elektromos és a mágneses jelenségek közötti megfeleltetést! Két $Q$ nagyságú, egymástól $a$ távolságra elhelyezett elektromos töltés között $F=\frac{1}{4\pi {\epsilon }_0}\frac{Q^2}{a^2}$ erő hat. Az egyik töltés terének energiasűrűsége a másik töltés helyén $\begin{array}{c}{\displaystyle w=\frac{{\epsilon }_0}{2}{E}^2=\frac{1}{32{\pi }^2{\epsilon }_0}\frac{Q^2}{a^4}\mathrm{.}}\end{array}$ Ezek szerint az erőt írhatjuk $F=8\pi w{a}^2$ alakban is. Ez a kifejezés bármely esetben használható két ellentétes előjelű, azonos nagyságú ponttöltés között fellépő erő meghatározására, így használhatjuk a mágneses ponttöltésekre is. A Gauss-törvény alapján egy $\Phi$ fluxusú mágneses ponttöltés által $a$ távolságra létrehozott indukció $B=\frac{\Phi }{4\pi a^2}$. Az energiasűrűség a ponttöltéstől $a$ távolságra $\begin{array}{c}{\displaystyle w=\frac{1}{2{\mu }_0}{B}^2=\frac{1}{32{\pi }^2{\mu }_0}\frac{{\Phi }^2}{a^4}\mathrm{,}}\end{array}$ amiből az $a$ távolságra lévő $\Phi$ fluxusú mágneses ponttöltések között fellépő erő $\begin{array}{c}{\displaystyle F=8\pi w{a}^2=\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{a^2}\mathrm{.}}\end{array}$ A négy ponttöltés közül az ellentétesek vonzzák egymást, a köztük fellépő erő $F_1=\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{{\ell }^2}$. Az átlósan elhelyezkedő azonos előjelű töltések közti taszítóerő normális komponense $\begin{array}{c}{\displaystyle F_2=\frac{\sqrt[]{2}}{2}\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{2{\ell }^2}\mathrm{.}}\end{array}$ Az eredő vonzó erő ezek alapján $\begin{array}{c}{\displaystyle F=2\left(F_1-F_2\right)=\frac{4-\sqrt[]{2}}{8\pi {\mu }_0}\frac{{\Phi }^2}{{\ell }^2}\mathrm{.}}\end{array}$   2. feladat. Kelvin csepegtetős gépe A rész. Egyetlen cső. i. A feladat szövege szerint a víz lassan csöpög ki a csőből: ez időben állandósult vízhozamra utal, ezért a csőben lévő vízoszlopra ható erők eredője (a cső falánál és a folyadékban fellépő belső súrlódás miatt) zérus. A vízcseppben uralkodó nyomás a külső légnyomásnál a felületi feszültség miatt $\Delta p=2\sigma /r$ értékkel nagyobb (itt $r$ a vízcsepp sugara). A cső végén függő, lassan hízó vízcseppre a következő négy erő hat: függőlegesen lefelé a $\frac{4}{3}\pi r^3\rho g$ nehézségi erő, a cső szája és a víz érintkezési vonalán a felületi feszültségből származó $2\pi r\sigma$ nagyságú, felfelé mutató erő, a $p_0$ külső légnyomásból származó (felfelé irányuló) erő és a vízcsepp csőhöz csatlakozó részén egy kis $d$ átmérőjű körlapon ható $p_0+\Delta p$ nyomásból származó, lefelé mutató erő. Könnyen belátható, hogy utóbbi két erő eredője $\frac{\pi }{4}{d}^2\Delta p$, ezt a $d$-ben másodrendűen kicsiny hatást $d\ll r$ miatt elhanyagolhatjuk. Közvetlenül a leválás előtt a vízcsepp jelentősen deformálódik: a csepp felső része és a cső között kicsiny, $d$ átmérőjű, hengeres nyak képződik. Ebben a pillanatban a ,,nyak'' által függőlegesen felfelé kifejtett $\pi d\sigma$ kapilláris erő éppen ellensúlyozza a vízcsepp súlyát, azaz $\begin{array}{c}{\displaystyle \pi d\sigma =\frac{4}{3}\pi r_{\underset{}{\overset{}{\text{max}}}}^3\rho g\mathrm{,}}\end{array}$ innen a csepp maximális sugara: $\begin{array}{c}{\displaystyle r_{\underset{}{\overset{}{\text{max}}}}=\sqrt[3]{\frac{3\sigma d}{4\rho g}}\mathrm{.}}\end{array}$   ii. A vízcsepp töltéseloszlása ($d\ll r$ miatt) jó közelítéssel egyenletes, így a csepp $\phi$ potenciálja egy $Q$ töltésű gömb potenciáljaként számolható: $\begin{array}{c}{\displaystyle \phi =\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r}\mathrm{,}}\end{array}$ ebből $Q=4\pi {\epsilon }_0\phi r$.   iii. A feltöltött gömbön kívül, felületének közelében $E=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}$ nagyságú térerősség uralkodik, a gömbön belül pedig zérus az elektromos térerősség. A gömb felületén lévő, $\Delta A$ felszínű kicsiny darabka töltése az egyenletes töltéseloszlás miatt $\Delta Q=\frac{\Delta A}{4\pi r^2}Q$, a rá ható erő pedig $\begin{array}{c}{\displaystyle \Delta F=\frac{1}{2}E\Delta Q=\frac{Q^2}{32{\pi }^2{\epsilon }_0{r}^4}\Delta A=\frac{{\epsilon }_0{\phi }^2}{2r^2}\Delta A\mathrm{.}}\end{array}$ (Az $\frac{1}{2}$-es szorzótényező ‐ kissé pongyolán fogalmazva ‐ onnan származik, hogy a térerősség csak a darabka külső oldalán $E$, a belső oldalon zérus, így átlagosan $E/2$ a darabka helyén a térerősség. Ugyanez a faktor jelenik meg egy síkkondenzátor lemezei között ható erő kifejezésében is.) A vízcseppet a felületi feszültség igyekszik összehúzni, a felületén lévő, egymást taszító töltések pedig igyekeznek kitágítani. Az elektromos taszításból származó erő $\frac{\Delta F}{\Delta A}$ értékkel csökkenti a csepp belsejében uralkodó nyomást. A csepp akkor szakad szét, ha ez a ,,negatív'' nyomás éppen megegyezik a görbületi nyomással: $\begin{array}{c}{\displaystyle \frac{{\epsilon }_0{\phi }_{\underset{}{\overset{}{\text{max}}}}^2}{2r^2}=\frac{2\sigma }{r}\mathrm{,}}\end{array}$ ebből a maximálisan alkalmazható potenciál ${\phi }_{\underset{}{\overset{}{\text{max}}}}=2\sqrt[]{\sigma r/{\epsilon }_0}$.   B rész. Két cső. i. Bár a cseppek potenciálja a földelés miatt nulla, a környező, hengeres elektródák hatása miatt mégis feltöltődnek. Vizsgáljuk meg a potenciál változását a következő, a bal oldali csepptől a jobb oldali cseppig vezető útvonalon: a bal oldali csepptől a bal oldali hengeres elektródáig $U$ a potenciálkülönbség, a bal oldali és a jobb oldali elektróda között $q/C$ a feszültség (hiszen a kondenzátoron át kell haladnunk), végül a jobb oldali elektróda és a jobb oldali csepp között (a szimmetria miatt és a töltések előjele miatt) ismét $U$ a feszültség. Útvonalunk kezdő- és végpontja egyaránt zérus potenciálú, tehát a feszültségek összegének is nullának kell lennie: $\begin{array}{c}{\displaystyle U+q/C+U=\mathrm{0,}}\end{array}$ azaz az azonos oldalon elhelyezkedő hengeres elektróda és csepp között $\begin{array}{c}{\displaystyle U=\pm q/\left(2C\right)}\end{array}$ a feszültség (az előjel attól függ, hogy a jobb vagy bal oldalt vizsgáljuk). Az A/ii. rész eredményét felhasználva, a $\phi =q/\left(2C\right)$ és $r=r_{\underset{}{\overset{}{\text{max}}}}$ helyettesítéssel megkapjuk az éppen leeső cseppek töltését: $\begin{array}{c}{\displaystyle Q=2\pi {\epsilon }_{0}q{r}_{\underset{}{\overset{}{\text{max}}}}/C\mathrm{.}}\end{array}$ ii. Az egységnyi idő alatt lecseppenő cseppek száma $n$, így a hengeres elektródák (vagyis a kondenzátor) töltése $\text{d}t$ idő alatt $\text{d}q=Qn\text{d}t$ értékkel növekszik. Az előző alkérdés eredményét felhasználva ez tovább alakítható: $\begin{array}{c}{\displaystyle \frac{\text{d}q}{\text{d}t}=\frac{2\pi {\epsilon }_0{r}_{\underset{}{\overset{}{\text{max}}}}n}{C}q\mathrm{,}}\end{array}$ ami egy előjeltől eltekintve a radioaktív bomlás differenciálegyenletére hasonlít. A jobb oldalon eltérő előjel azt eredményezi, hogy a kondenzátor töltése a radioaktív atommagok számával ellentétben nem exponenciálisan csökken, hanem exponenciálian növekszik az idővel: $\begin{array}{c}{\displaystyle q\left(t\right)=q_0{e}^{\gamma t}\mathrm{,}\text{ahol}\gamma =\frac{2\pi {\epsilon }_0{r}_{\underset{}{\overset{}{\text{max}}}}n}{C}=\frac{\pi {\epsilon }_{0}n}{C}\sqrt[3]{\frac{6\sigma d}{\rho g}}\mathrm{.}}\end{array}$   iii. A leeső cseppek akkor érhetik el az alattuk elhelyezkedő edényeket, ha az $mgH$ gravitációs helyzeti energiájuk elég nagy az elektrosztatikus taszítás legyőzéséhez. Közvetlenül a leszakadás után a $Q$ töltésű csepp a hengeres elektróda által létrehozott $q/\left(2C\right)$ potenciált érzi, amikor pedig az alatta lévő, vízzel telt edénybe érkezik, $-q/\left(2C\right)$ potenciálú helyre kerül. Az edény elérésének feltétele tehát: $\begin{array}{c}{\displaystyle \frac{q}{C}Q\le mgH\mathrm{,}\text{ahol}Q=\frac{2\pi {\epsilon }_{0}q{r}_{\underset{}{\overset{}{\text{max}}}}}{C}\mathrm{.}}\end{array}$ Ebből a kondenzátor $U_C=q/C$ feszültségének legnagyobb értéke: $\begin{array}{c}{\displaystyle U_C^{\underset{}{\overset{}{\text{max}}}}=\sqrt[]{\frac{mgH}{2\pi {\epsilon }_0{r}_{\underset{}{\overset{}{\text{max}}}}}}\mathrm{.}}\end{array}$ Az A/i. rész eredményét felhasználva a végeredmény: $\begin{array}{c}{\displaystyle U_C^{\underset{}{\overset{}{\text{max}}}}=\sqrt[6]{\frac{{\sigma }^2{d}^2{H}^3\rho g}{6{\epsilon }_0}}\mathrm{.}}\end{array}$   3. feladat. Csillagkezdemény kialakulása i. A kezdeti szakaszban a hőmérséklet nem változik. Így a Boyle‐Mariotte-törvény alapján: $\begin{array}{c}{\displaystyle \frac{p_1}{p_0}=\frac{V_0}{V_1}={\left(\frac{r_0}{r_1}\right)}^3=8.}\end{array}$   ii. A folyamat kezdetén a gáz nyomásából származó erők elhanyagolhatók a gravitációs erőhöz képest. Tekintsünk egy kicsiny gáztérfogatot a gázfelhő szélén. Ismert, hogy egy gömbszimmetrikus tömegeloszlás gravitációs tere a gömbön kívül (és annak felületén) megegyezik a gömb középpontjába helyezet (azonos tömegű) tömegpont gravitációs terével. Így a gáztérfogatunk kezdeti gyorsulása $g\approx Gm/r_0^2$. Mivel a gravitációs erő nem változik lényegesen, a gyorsulást közelíthetjük ezzel az állandó értékkel. Ebben a közelítésben egyenletesen gyorsuló mozgásról beszélhetünk. A négyzetes úttörvényből az idő könnyen kifejezhető: $\begin{array}{c}{\displaystyle t_2\approx \sqrt[]{\frac{2\left(r_0-r_2\right)}{g}}=\sqrt[]{\frac{2r_0^2\left(r_0-r_2\right)}{Gm}}=\sqrt[]{\frac{0\mathrm{,}1r_0^3}{Gm}}\mathrm{.}}\end{array}$   Megjegyzés. Érdemes észrevenni, hogy ez az idő csak a gázfelhő sűrűségétől függ. Ez azt jelenti, hogy a gázfelhő belsejében kiszemelt kicsiny gáztérfogatra is igaz, hogy $t_2$ idő alatt csökken a középponttól mért távolsága 5%-kal. Hasonló okoskodással belátható, hogy ez a későbbi (nem nulla kezdősebességű) mozgásszakaszokra is érvényes, és emiatt a kezdetben homogén anyageloszlású gázfelhő mindaddig homogén marad, amíg a gáz nyomása elhanyagolható.   iii. Továbbra is feltételezzük, hogy a kicsiny gáztérfogatunk mozgásában a gravitáción kívüli hatásokat elhanyagolhatjuk. A feladat szövege azt sugallja, hogy az esési pályát egy elfajult ellipszispályának tekintsük, melynek fél nagytengelye $r_0/2$ (lásd a 4. ábrát). 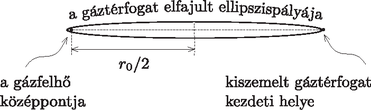  4. ábra   Kepler III. törvényéből következik, hogy a pálya periódusideje megegyezik egy $r_0/2$ sugarú körpálya $T$ periódusidejével, amit az egyenletes körmozgás mozgásegyenletéből könnyen ki lehet számítani: $\begin{array}{c}{\displaystyle {\left(\frac{2\pi }{T}\right)}^2\frac{r_0}{2}=\frac{Gm}{{\left(r_0/2\right)}^2}\mathrm{,}\text{ahonnan}T=2\pi \sqrt[]{\frac{r_0^3}{8Gm}}\mathrm{.}}\end{array}$ A feladat szövegéből kitűnik, hogy a végső sugár sokkal kisebb, mint a kezdeti, ezért az összeomlás idejét közelíthetjük a kiszámolt periódusidő felével: $\begin{array}{c}{\displaystyle t=\frac{T}{2}=\pi \sqrt[]{\frac{r_0^3}{8Gm}}\mathrm{.}}\end{array}$   Megjegyzés. A gázfelhő gravitációs összeroskadásának idejét úgy is megkaphatjuk, hogy az energiamegmaradás törvényét használva kiszámítjuk a sebesség helyfüggését: $\begin{array}{c}{\displaystyle \frac{v^2}{2}-\frac{Gm}{r}=E\left(=-\frac{Gm}{r_0}\right)\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle -\frac{\text{d}r}{\text{d}t}=v\left(r\right)=\sqrt[]{2E+\frac{2Gm}{r}}\mathrm{,}}\end{array}$ majd a sebesség reciprokát integráljuk a teljes pályára: $\begin{array}{c}{\displaystyle t=\underset{0}{\overset{r_0}{\int }}\frac{\text{d}r}{\sqrt[]{2E+\frac{2Gm}{r}}}\mathrm{.}}\end{array}$ Az integrál (melynek kiszámítása a verseny korlátozott ideje alatt nyilván nem várható el) ugyanazt az eredményt adja, mint a Kepler-törvényekre hivatkozó megoldás.   iv. Mivel a gáz hőmérséklete nem változik, azért a gáz által kisugárzott hő a gázon végzett munkával egyenlő. A gáz izoterm állapotváltozása során a végzett munka: $\begin{array}{c}{\displaystyle W=-\underset{V_0}{\overset{V_3}{\int }}p\left(V\right)\text{d}V\mathrm{,}}\end{array}$ ahol a nyomás a $pV=\frac{m}{\mu }R{T}_0$ gáztörvényből számolható. A kisugárzott hő eszerint $\begin{array}{c}{\displaystyle Q=W=-nR{T}_0\underset{V_0}{\overset{V_3}{\int }}\frac{1}{V}\text{d}V=R{T}_0\frac{m}{\mu }\text{ln}\frac{V_0}{V_3}=3R{T}_0\frac{m}{\mu }\text{ln}\frac{r_0}{r_3}\mathrm{.}}\end{array}$   Megjegyzések. 1. A felhasznált munkaképlet arra az esetre vonatkozik, amikor a gáz egyensúlyi állapotokon keresztül jut el egyik állapotból a másikba. Ez a jelen esetben nem teljesül, de ennél jobb becslést nem lehet adni. 2. Sokan ott hibáztak, hogy a gravitációs energia teljes változásával tették egyenlővé a kisugárzott hőt. Ez csak akkor lenne igaz, ha a nyomás a gravitációval azonos nagyságú lenne, itt viszont elhanyagolható. A feladat szövegében megadott $Gm\mu /r_0\gg R{T}_0$ egyenlőtlenséggel könnyű belátni, hogy a kisugárzott hő elhanyagolható a gravitációs energiaváltozáshoz képest.   v. Az összeroskadás ebben a szakaszban adiabatikus. Az adiabatikus állapotváltozásra igaz, hogy $p{V}^{\gamma }=$ állandó. Ebből és a gáztörvényből következik, hogy $T{V}^{\gamma -1}=$ állandó. Ezt felhasználva: $\begin{array}{c}{\displaystyle T=T_0{\left(\frac{V_3}{V}\right)}^{\gamma -1}=T_0{\left(\frac{r_3}{r}\right)}^{3\gamma -3}\mathrm{.}}\end{array}$   vi. Az összeroskadás $r_3\to r_4$ szakaszában a gravitációs energia és a meglévő mozgási energia alakul át a gáz belső energiájává. A mozgási energia megegyezik az $r_0\to r_3$ szakaszon történő gravitációs energiaváltozás nagyságával. A gravitációs energiaváltozást a következő formulával becsülhetjük: $\begin{array}{c}{\displaystyle \Delta E_{\text{g}}=-G\frac{m^2}{r_4}-\left(-G\frac{m^2}{r_0}\right)\approx -G\frac{m^2}{r_4}\mathrm{.}}\end{array}$ (A pontosabb, integrálással meghatározható energiaváltozás ettől a becsléstől egy $\frac{3}{5}$-ös szorzótényezőben különbözik.) A belső energia megváltozása: $\begin{array}{c}{\displaystyle \Delta E_{\text{b}}=\frac{f}{2}nR{T}_4-\frac{f}{2}nR{T}_0\approx \frac{f}{2}nR{T}_4\approx nR{T}_4\mathrm{.}}\end{array}$ A fenti közelítéseknél kihasználtuk, hogy $r_4\ll r_0$ és $T_4\gg T_0$; az $f/2$ tényező helyébe pedig azért írtunk 1-et, mert csupán nagyságrendi becslésre törekszünk; az egységnyi nagyságú szorzótényezőket nem vesszük számításba.) A két energiaváltozás nagyságát egyenlővé téve ‐ és a hőmérsékletet a felhő sugarával kifejezve ‐ kapjuk: $\begin{array}{c}{\displaystyle G\frac{m^2}{r_4}\approx \frac{m}{\mu }R{T}_0{\left(\frac{r_3}{r_4}\right)}^{3\gamma -3}\mathrm{.}}\end{array}$ Innen a keresett méret és hőmérséklet kifejezhető: $\begin{array}{c}{\displaystyle r_4\approx r_3{\left(\frac{R{T}_0{r}_3}{\mu mG}\right)}^{\frac{1}{3\gamma -4}}\mathrm{,}{T}_4\approx T_0{\left(\frac{R{T}_0{r}_3}{\mu mG}\right)}^{\frac{3\gamma -3}{4-3\gamma }}\mathrm{.}}\end{array}$   Megjegyzések. 1. Az egyensúlyba került gázfelhő közepén kialakuló nyomást (közelítően, de nagyságrendileg helyesen) kétféleképpen is kiszámíthatjuk: egyrészt a ($\varrho$ sűrűségű) gáz hidrosztatikai nyomásaként: $\begin{array}{c}{\displaystyle p\approx \varrho r_4\cdot \frac{Gm}{r_4^2}\mathrm{,}}\end{array}$ másrészt a gáztörvény felhasználásával: $\begin{array}{c}{\displaystyle p\approx \frac{\varrho }{\mu }R{T}_4\mathrm{.}}\end{array}$ A két kifejezés jobb oldalát egyenlővé téve (valamint $T_4$ és $r_4$ korábban kiszámított kapcsolatát is felhasználva) megkapjuk $T_4$ és $r_4$ fentebb levezetett kifejezéseit. 2. Sok versenyző (a magyar diákok közül is többen) a virtuális munka elvét használták. Eszerint egy test akkor van egyensúlyi helyzetben, ha egy kicsiny elképzelt (virtuális) kitérítés esetén a testen végzett munkák összege nulla. A jelen esetre alkalmazva ez azt jelenti, hogy kicsi sugárváltozás esetén a felszabaduló gravitációs energia éppen fedezi a gáz belső energia növekedését. Az így számolt képletek egy konstans szorzózényezőben térnek el a fenti eredményektől. Az eltérés okát egy egyszerű mechanikai példával szemléltethetjük. Ha egy nyújtatlan rugóra egy testet akasztunk, és felírjuk az energia-megmaradás törvényét, akkor a rezgőmozgás alsó és felső maximális kitérési helyét kapjuk meg, a virtuális munka elvével pedig az egyensúlyi helyzetet találjuk meg.   Kísérleti feladatok   1. feladat. A víz mágneses permeabilitása A sztatikus mágneses mező hatása a legtöbb anyagra (a ferromágneses anyagokon kívül) igen gyenge. Ez alól a víz sem kivétel: még ha egy erős neodímium mágnest is helyezünk a vízfelszín közelébe, annak alakváltozása szabad szemmel alig észrevehető. Ebben a mérési feladatban a víz mágneses permeabilitását kellett meghatározni egy tálkában lévő erős mágnest éppen ellepő víz felületének megfigyelésével. A víz felületének letapogatása precíziós mérési összeállítást kívánt. Egy asztalon helyezkedett el a tálca, benne az alacsony, henger alakú erős mágnessel és a vízzel. A vízfelszín kb. 1 mm-rel állt magasabban a mágnes tetejénél. A felszín alakját egy ferdén beállított, vízszintesen tolómérővel mozgatható lézerceruzából érkező nyalábbal lehetett letapogatni. A visszaverődés után a lézerfolt egy függőlegesen rögzített milliméterpapíron (ernyőn) vált észlelhetővé. A versenyzők a lézerceruza pozíciójának függvényében mérték a fényfolt helyzetét az ernyőn; ezekből az adatokból és a szükséges geometriai méretek leméréséből ‐ némi gondolkodás és számolás után ‐ a vízfelszín pontos alakja meghatározható. Az eredményekből kiderült, hogy a mágnes fölötti részen a víz (körülbelül 100 $\mu$m-es mértékben) behorpadt. 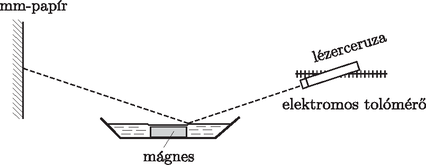  5. ábra   A vízfelszín $h$ behorpadásának mért értékéből és a henger alakú mágnes által a körlapon létrehozott indukció (a feladatban megadott) $B$ nagyságából következtetni kellett a víz relatív permeabilitására. Ehhez többféle gondolatmenettel is eljuthatunk, egy lehetséges út a következő. A felszín besüllyedése a mágnes fölött a víznek egy $A$ területű részén történik. Képzeljük el, hogy a felület behorpadását $h$-ról $h+\Delta h$ értékre növeljük! Ekkor a mágnes fölött $A\Delta h$ térfogatú térrészben az addig jelenlévő $\mu$ relatív permeabilitású víz helyére 1 relatív permeabilitású levegő kerül, így a mágneses mező energiaváltozása: $\begin{array}{c}{\displaystyle \Delta E{}_{\text{mágn.}}=-\left(\frac{B^2}{2\mu {\mu }_0}-\frac{B^2}{2{\mu }_0}\right)A\Delta h\approx -\frac{B^2}{2{\mu }_0}\left(1-\mu \right)A\Delta h}\end{array}$ (itt kihasználtuk, hogy $1-\mu \ll 1$). Másrészt a gondolatkísérletünk során a tálkában lévő víz gravitációs helyzeti energiája megnőtt, amit úgy számolhatunk, mintha $A\Delta h$ térfogatú víz a felszín mágnestől távoli részére, azaz $h$-val magasabbra került volna: $\begin{array}{c}{\displaystyle \Delta E_{\text{pot.}}=\varrho ghA\Delta h\mathrm{,}}\end{array}$ itt $\varrho$ a víz sűrűsége. Egyensúly esetén a virtuális munkák összege zérus, azaz $\Delta E_{\text{mágn.}}+\Delta E_{\text{pot.}}=0$, amiből: $\begin{array}{c}{\displaystyle 1-\mu =\frac{2{\mu }_0\varrho gh}{B^2}\mathrm{.}}\end{array}$ A feladatban megadott $B$ és a mért $h$ adat felhasználásával $1-\mu$-re $1\cdot {10}^{-5}$ körüli érték adódott, ami összhangban van az irodalmi érték nagyságrendjével. A víz relatív permeabilitása tehát kicsit kisebb 1-nél, az ilyen anyagokat diamágneseknek nevezzük. Ebben a mérési feladatban a legnagyobb nehézséget a megfelelő pontosságú és számú adat felvétele, valamint a precíz kiértékelés jelentette. Kihívás volt a relatív permeabilitás meghatározására vonatkozó összefüggés felírása is. Összességében ez a feladat (a 2-es számú méréssel ellentétben) inkább a kísérletező készséget, gyakorlottságot mérte, megoldása nagy ötleteket nem igényelt.   2. feladat. Nemlineáris fekete doboz Ebben a mérésben a 6. ábrán látható nemlineáris elemet is tartalmazó elektromos fekete dobozt vizsgálták a versenyzők. 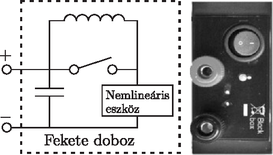  6. ábra   A fekete dobozban egy ismeretlen, nemlineáris karakterisztikájú áramköri elem, egy elektrolitkondenzátor és egy ‐ kapcsolóval rövidre zárható ‐ $10\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>μ</mi></math>H}$ induktivitású tekercs található. A méréshez egy áramforrás, egy ,,intelligens'' (adatgyűjtő funkciókkal rendelkező) multiméter és összekötő vezetékek állnak még rendelkezésre.   7. ábra     8. ábra   A multiméter ‐ két különböző bemeneten ‐ egyszerre tud feszültséget és áramerősséget mérni. Ezekkel együtt kiírja és elmenti a feszültség és az áramerősség változási sebességét (idő szerinti deriváltját), a $P=UI$ teljesítményt, az $R=\frac{U}{I}$ ellenállást és a mérés időpontját. Ezzel nagyon meggyorsítja és megkönnyíti a feladat elvégzéséhez szükséges adatok összegyűjtését.   A rész. Induktivitás nélküli áramkör. Ebben a részben a tekerccsel párhuzamosan kötött kapcsolót be kell kapcsolni, így a tekercs rövidre van zárva (mintha ott se lenne). Az elektrolitkondenzátor kapacitása kb. $2\text{F}$ ‐ ezt méréssel igazolni kell. Ezután ‐ először a kondenzátor kapacitását feszültségfüggetlennek feltételezve ‐ fel kell venni és ábrázolni kell az ismeretlen nemlineáris áramköri elem áram‐feszültség karakterisztikáját. Az eredmény a 9. ábrán látható (folytonos vonal). Megfigyelhető, hogy az $I\left(U\right)$ karakterisztika egy szakaszon csökken, tehát itt az áramköri elem differenciális ellenállása (amit a $\frac{\text{d}U}{\text{d}I}$ deriválttal értelmezünk) negatív. Ez az áramkörben instabilitásokat okozhat, ahogy az majd a következő részben látható is lesz. 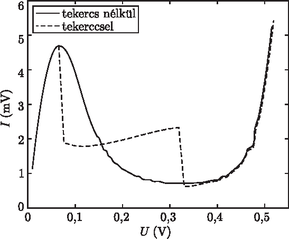  9. ábra   Ennek a résznek a végén ki kell mérni a kondenzátor kapacitásának (kismértékű) feszültségfüggését. Itt az a buktató, hogy ehhez ‐ természetesen ‐ nem lehet felhasználni olyan eredményeket, amelyeket a kapacitás állandóságát feltételezve kaptunk. A trükk az, hogy a kondenzátor feltöltése és kisütése közben is kell méréseket végezni. (Részletek az olimpia honlapján: http://www.ipho2012.ee/solutions/.)   B rész. Áramkör induktivitással. A kapcsoló kinyitásával a tekercs sorba kötődik a nemlineáris áramköri elemmel. Most ismét a nemlineáris elem $I\left(U\right)$ karakterisztikáját kell felvenni és értelmezni. Az előző ábrán látható, hogy a görbe (szaggatott vonal) a pozitív differenciális ellenállású tartományokban hibahatáron belül megegyezik az előző részben mért görbével. A negatív differenciális ellenállású tartományban azonban lényegesen eltérő: ugrásszerű változás után közel állandó értékű lesz, majd ismét ugrásszerűen tér vissza az eredeti görbéhez. Mi ennek az oka? A nemlineáris elemnek kicsiny ($\approx 1\text{nF}$) kapacitása is van (ez szerepelt a feladat szövegében), így a tekerccsel egy néhány MHz-es frekvenciájú soros rezgőkört alkotnak. A negatív differenciális ellenállás miatt ez a rezgés nem csillapodik, hanem folyamatosan erősödik, amplitúdójának csak a tápfeszültség szab határt. Az egyenáramú mérőműszer azonban ennek a rezgésnek csak az átlagértékét méri ‐ ez látszik a grafikonon.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Sarlós Ferenc, Vankó Péter, Vigh Máté</span>}}\hfill \end{array}}$ 1Az elméleti feladatok szövegét a múlt havi számunkban közöltük.