Cím:	Megoldásvázlatok a 2007/2. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2007/március, 140 - 144. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

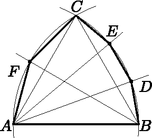
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Az $ABC$ szabályos háromszögben az $A$ középpontú, $AB$ sugarú kör kisebbik $BC$ ívének $B$-hez közelebbi harmadolópontja $D$, $C$-hez közelebbi harmadolópontja pedig $E$. A $B$ középpontú $AB$ sugarú kör kisebbik $AC$ ívének felezőpontja $F$. Mekkorák az $ABDECF$ hatszög belső szögei?  (11 pont)   Megoldás. Az $ABC$ szabályos háromszög minden szöge ${60}^{\circ }$-os. Az $AFB$ és az $FBC$ egyenlőszárú háromszögnek $B$-nél ${30}^{\circ }$-os szárszöge van, ezért az alapokon fekvő szögeik ${75}^{\circ }$-osak. A $CAE$, az $EAD$ és a $DAB$ egyenlőszárú háromszögeknek $A$-nál ${20}^{\circ }$-os szárszögük van, ezért az alapokon fekvő szögeik ${80}^{\circ }$-osak. Ezek alapján a szögek a következők:     $A$-nál ${75}^{\circ }$, $B$-nél ${80}^{\circ }$, $D$-nél és $E$-nél $2\cdot {80}^{\circ }$, azaz ${160}^{\circ }$, $C$-nél ${80}^{\circ }+{75}^{\circ }-{60}^{\circ }={95}^{\circ }$, $F$-nél $2\cdot {75}^{\circ }$, azaz ${150}^{\circ }$.   2. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \sqrt[]{x^2-2x-15}\cdot \text{lg}\left(5-x\right)\cdot \text{sin}\left(x-\frac{\pi }{3}\right)=0.}\end{array}$ (12 pont)   Megoldás. A négyzetgyök értelmezése miatt: $x^2-2x-15\ge 0$, azaz $x\in \left]-\infty ;-3\right]\cup \left[5;\infty \right[$, a logaritmus definíciója miatt: $x\in \left]-\infty ;5\right[$. Vagyis a feladat értelmezési tartománya: $x\in \left]-\infty ;-3\right]$. A három tényező zérushelyeit külön-külön megvizsgáljuk. Az első tényező zérushelyei a $-3$ és az 5, de a feladat értelmezési tartományának csak a $-3$ felel meg. A második tényező zérushelye a 4, de ez nincs benne az értelmezési tartományban. A harmadik tényező zérushelyei: $x=\frac{\pi }{3}+k\pi$, ahol $k$ egész szám. A feladat értelmezési tartománya miatt azonban $k<-1$. A megoldás: $x_1=-3$, $x_2=\frac{\pi }{3}+k\pi$, ahol $k<-1$ egész szám.   3. Egy vihar után tizenkét telefonvonal közül négy nem működik. Ekkor négy vonalon megpróbálunk telefonálni. Mennyi annak a valószínűsége, hogy a négy hívásból pontosan kettő lesz sikeres?  (14 pont)   Megoldás. Kiszámítjuk az összes lehetőséget. A 12 vonal közül négyen próbálunk telefonálni, így a 12-ből 4-et kell kiválasztani (a sorrend nem számít). Ezt $\left(\genfrac{}{}{0ex}{}{12}{4}\right)=495$-féleképpen tehetjük meg. Most a vizsgált esemény szempontjából kedvező eseteket számoljuk össze. A két sikeres hívás a nyolc jó vezetéken, a két sikertelen hívás a négy rossz vezetéken történik (a sorrend itt sem számít). Ez $\left(\genfrac{}{}{0ex}{}{8}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)=28\cdot 6=168$-féleképpen történhet. A keresett valószínűség: $p=\frac{168}{495}\approx 0\mathrm{,}34$.   4. Mutassuk meg, hogy az $\left\{a_n\right\}$ számtani sorozatban: $\begin{array}{c}{\displaystyle \left(x-y\right)a_z+\left(y-z\right)a_x=\left(x-z\right)a_y\mathrm{,}}\end{array}$ ahol $x$, $y$ és $z$ természetes számok.  (14 pont)   Megoldás. Fejezzük ki az első tag és a különbség segítségével a feladatban szereplő tagokat: $\begin{array}{c}{\displaystyle a_x=a_1+\left(x-1\right)d\mathrm{,}{a}_y=a_1+\left(y-1\right)d\mathrm{,}{a}_z=a_1+\left(z-1\right)d\mathrm{.}}\end{array}$ Írjuk fel a páronkénti különbségüket: $\begin{array}{c}{\displaystyle a_x-a_y=\left(x-y\right)d\mathrm{,}{a}_y-a_z=\left(y-z\right)d\mathrm{,}{a}_x-a_z=\left(x-z\right)d\mathrm{.}}\end{array}$ Ha $d\ne 0$, akkor ezeket a következő alakban is írhatjuk: $\begin{array}{c}{\displaystyle \frac{a_x-a_y}{d}{a}_z=\left(x-y\right)a_z\mathrm{,}\frac{a_y-a_z}{d}{a}_x=\left(y-z\right)a_x\mathrm{,}\frac{a_x-a_z}{d}{a}_y=\left(x-z\right)a_y\mathrm{.}}\end{array}$ Mivel az első kettő összege a harmadikat adja, azért a bizonyítandó állítást kaptuk. Ha $d=0$, akkor $a_x=a_y=a_z$, az állítás ekkor is igaz.   II. 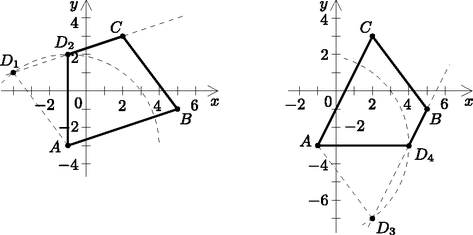rész   5. Egy húrtrapéz három csúcsának koordinátája a következő: $\left(-1;-3\right)$; $\left(5;-1\right)$; $\left(2;3\right)$. Határozzuk meg a negyedik csúcs koordinátáit, ha az ismeretlen pont két koordinátájának szorzata negatív.  (16 pont)   Megoldás. A feladat feltételei szerint a negyedik pontnak a II. vagy a IV. negyedben kell lennie. Legyen $A\left(-1;-3\right)$; $B\left(5;-1\right)$; $C\left(2;3\right)$. 1. eset: $AB$ a szár. Belátható, hogy ekkor a $D$ csúcs a III. negyedben van. 2. eset: $AB$ a hosszabb alap, $BC$ a szár, aminek hossza 5. A $C$ pontra illeszkedő $AB$-vel párhuzamos egyenes egyenlete: $x-3y=-7$. Ez az egyenes az $A$ középpontú 5 sugarú körből (amelynek egyenlete: ${\left(x+1\right)}^2+{\left(y+3\right)}^2=25$) kimetszi a $D$ pontot. Két metszéspontot kapunk. A $D_1\left(-4;1\right)$ nem jó, mert ekkor a négyszög olyan paralelogramma, ami nem húrtrapéz. A $D_2\left(-1;2\right)$ minden feltételnek megfelel.     3. eset: $AC$ a hosszabb alap, $BC$ a szár, aminek hossza 5. A $B$ pontra illeszkedő $AC$-vel párhuzamos egyenes egyenlete: $2x-y=11$. Ez az egyenes az $A$ középpontú 5 sugarú körből kimetszi a $D$ pontot. Két metszéspontot kapunk. A $D_3\left(2;-7\right)$ nem jó, mert ekkor a négyszög olyan paralelogramma, ami nem húrtrapéz. A $D_4\left(4;-3\right)$ minden feltételnek megfelel. Vagyis a $\left(-1;2\right)$, illetve a $\left(4;-3\right)$ koordinátájú pont lehet a húrtrapéz negyedik csúcsa.   6. Egy iskola két párhuzamos osztálya közös dolgozatot írt, az elérhető legmagasabb pontszám $120$ pont volt. Az $A$ osztályban $74$ pont, a $B$ osztályban $84$ pont lett az átlag. Az $A$ osztályos lányok átlaga $71$ pont, a $B$ osztályos lányok pedig $81$ pontot értek el átlagosan. Az összes lány átlaga $79$ pont lett. A fiúk átlaga az $A$ osztályban $76$ pont, a $B$ osztályban pedig $90$ pont. Mennyi a két osztályban az összes fiú átlagpontszáma?  (16 pont)   Megoldás. Készítsünk egy táblázatot a rendelkezésünkre álló adatok alapján. A két osztályban az összes fiú átlagpontszáma legyen $x$. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccc}{\displaystyle }\hfill & \hfill {\displaystyle \text{lányok}}\hfill & \hfill {\displaystyle \text{fiúk}}\hfill & \hfill {\displaystyle \text{osztály}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{71}}\hfill & \hfill {\displaystyle \text{76}}\hfill & \hfill {\displaystyle \text{74}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{81}}\hfill & \hfill {\displaystyle \text{90}}\hfill & \hfill {\displaystyle \text{84}}\hfill \\ {\displaystyle \text{ összes}}\hfill & \hfill {\displaystyle \text{79}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill \end{array}}}\end{array}$ Legyen az $A$ osztályban $a$ lány, a $B$ osztályban $b$ lány, az $A$ osztályban $c$ fiú, a $B$ osztályban $d$ fiú. Ekkor a táblázat első sora alapján: $\begin{array}{c}{\displaystyle 71a+76c=74\left(a+c\right)\mathrm{.}}\end{array}$ (1) A táblázat második sora alapján: $\begin{array}{c}{\displaystyle 81b+90d=84\left(b+d\right)\mathrm{.}}\end{array}$ (2) A táblázat első oszlopa alapján: $\begin{array}{c}{\displaystyle 71a+81b=79\left(a+b\right)\mathrm{.}}\end{array}$ (3) A táblázat második oszlopa alapján: $\begin{array}{c}{\displaystyle 76c+90d=x\left(c+d\right)\mathrm{,}\text{ vagyis: }x=\frac{76c+90d}{c+d}\mathrm{.}}\end{array}$ (4) ${\displaystyle \begin{array}{cccc}{\displaystyle \text{ Az (1), (2) és (3) egyenleteket rendezzük:}}\hfill & {\displaystyle \text{(1)-ből:}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">=</mo><mn>1</mn><mn>,</mn><mn>5</mn><mi>a</mi></math>;}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{(2)-ből:}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math>}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">=</mo><mn>0</mn><mn>,</mn><mn>5</mn><mi>b</mi></math>;}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{(3)-ból:}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">=</mo><mn>4</mn><mi>a</mi></math>.}}\hfill \end{array}}$ Vagyis $d=0\mathrm{,}5\cdot 4a=2a$. Alkalmazzuk (4)-ben a $c=1\mathrm{,}5a$ és a $d=2a$ helyettesítéseket: $\begin{array}{c}{\displaystyle x=\frac{76c+90d}{c+d}=\frac{76\cdot 1\mathrm{,}5a+90\cdot 2a}{1\mathrm{,}5a+2a}=\frac{294a}{3\mathrm{,}5a}=84.}\end{array}$ A két osztályban az összes fiú átlagpontszáma 84.   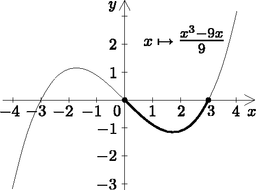7. Egy kis patak vízmélységét a folyás irányára merőlegesen az $f:\left[0;3\right]\to \text{R}$, $x\mapsto \frac{x^3-9x}{9}$ függvény adja meg (ahol az egységek métert jelentenek). $a)$ A patak szélétől hány méterre a legmélyebb a víz? $b)$ Mekkora a legnagyobb vízmélység? $c)$ Mekkora a patak percenkénti vízhozama, ha a folyási sebességét $0\mathrm{,}5\frac{\text{m}}{\text{s}}$-nak vehetjük?   Megoldás. $a)$ A függvény minimumhelyét keressük. Vegyük a függvény deriváltját: $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=\frac{1}{9}\left(3x^2-9\right)=\frac{1}{3}\left(x^2-3\right)\mathrm{.}}\end{array}$ A $\left[0;3\right]$ intervallumon egyetlen zérushelye van: $x=\sqrt[]{3}$. Itt a derivált előjelet vált, negatívból pozitív lesz, ezért a függvénynek az $x=\sqrt[]{3}$ a minimumhelye. Vagyis a patak egyik szélétől $\sqrt[]{3}$, a másik szélétől $3-\sqrt[]{3}$ méterre a legmélyebb a víz.     $b)$ A legnagyobb vízmélységet akkor kapjuk, ha a függvény minimumértékét kiszámítjuk. $\begin{array}{c}{\displaystyle f\left(\sqrt[]{3}\right)=\frac{{\left(\sqrt[]{3}\right)}^3-9\sqrt[]{3}}{9}=\frac{3\sqrt[]{3}-9\sqrt[]{3}}{9}=-\frac{2}{3}\sqrt[]{3}\approx -1\mathrm{,}15.}\end{array}$ Vagyis kb. 1,15 méter a legnagyobb vízmélység. $c)$ A patak keresztmetszetének területét a következő integrál adja: $\begin{array}{c}{\displaystyle \underset{0}{\overset{3}{\int }}\frac{9x-x^3}{9}dx=\frac{1}{9}{\left[\frac{9x^2}{2}-\frac{x^4}{4}\right]}_0^3=\frac{1}{9}\left(\frac{81}{2}-\frac{81}{4}\right)=2\mathrm{,}25.}\end{array}$ Vagyis 2,25 m${}^2$ a keresztmetszete a vizsgált helyen a pataknak, így a percenkénti vízhozam $0\mathrm{,}5\cdot 60\cdot 2\mathrm{,}25{\text{m}}^3=67\mathrm{,}5{\text{m}}^3$.   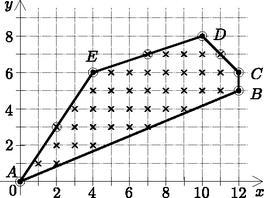8. Egy ötszög csúcsainak koordinátája: $A\left(0;0\right)$, $B\left(12;5\right)$, $C\left(12;6\right)$, $D\left(10;8\right)$, $E\left(4;6\right)$. $a)$ Hány rácspont található az ötszög határvonalán? $b)$ Hány rácspont található az ötszög belsejében? $c)$ A rácspontokra rajzolt sokszögek területét meghatározhatjuk a következő képlettel: $t=\frac{h+2b-2}{2}$, ahol $h$ a határvonalon, $b$ a belsejében lévő rácspontok számát jelöli. Mennyi ezen képlet szerint a feladatban szereplő ötszög területe? $d)$ Határozzuk meg a fenti képlet ismerete nélkül az ötszög területét.  (16 pont)   Megoldás. $a)$ Az $AB$ és a $BC$ szakaszokon nincs rácspont, a $CD$, a $DE$ és a $AE$ szakaszokon pedig 1‐1 db van. A csúcspontokkal együtt összesen 8 db van. (Ahol bizonytalanok vagyunk a döntésben, hogy a rácspont illeszkedik-e a szakaszra, ott a két pontra illeszkedő egyenes egyenletével gyorsan lehet dönteni.)     $b)$ Az egyenesek ismeretében az 1, 2, 3, 4, 5, 6, 7 ordinátákhoz rendre 2, 3, 5, 7, 8, 7, 3 pont tartozik. Vagyis összesen 35 rácspont van az ötszög belsejében. $c)$ Számításaink szerint: $h=8$, $b=35$. Ezeket a megadott képletbe behelyettesítve: $\begin{array}{c}{\displaystyle t=\frac{h+2b-2}{2}=\frac{8+2\cdot 35-2}{2}=38.}\end{array}$ $d)$ Az ötszög befoglalható egy 12-szer 8-as téglalapba. A téglalapból négy derékszögű háromszöget és egy kis téglalapot kell levágnunk, hogy az $ABCDE$ ötszöget kapjuk. Vagyis: $t=96-30-2-6-12-8=38$.   9. Oldjuk meg a következő egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \text{log}{}_3\text{log}{}_2\left(4x^2\right)+\text{log}{}_{\frac{1}{3}}\text{log}{}_{\frac{1}{2}}\frac{1}{x}=1.}\end{array}$ (16 pont)   Megoldás. A feladat értelmezési tartománya: $x>0$. Végezzük el a következő átalakításokat: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_3\text{log}{}_2\left(4x^2\right)-\text{log}{}_3\text{log}{}_{\frac{1}{2}}{\left(x\right)}^{-1}}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle \text{log}{}_3\text{log}{}_2\left(4x^2\right)-\text{log}{}_3\text{log}{}_{2}x}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle \text{log}{}_3\frac{\text{log}{}_2\left(4x^2\right)}{\text{log}{}_{2}x}}& {\displaystyle =1=\text{log}{}_{3}3.}\hfill \end{array}}$ A logaritmus függvény kölcsönös egyértelműsége miatt: $\begin{array}{c}{\displaystyle \frac{\text{log}{}_2\left(4x^2\right)}{\text{log}{}_{2}x}=\mathrm{3,}\text{ vagyis }\text{log}{}_2\left(4x^2\right)=3\text{log}{}_{2}x\mathrm{.}}\end{array}$ Ezt így is írhatjuk: $\text{log}{}_2\left(4x^2\right)=\text{log}{}_2{x}^3$, azaz $4x^2=x^3$. Vagyis az egyenlet egyedüli megoldása az értelmezési tartományon: $x=4$.