Cím:	Csavarási inga: forgási rezgése
Füzet:	1967/szeptember, 34 - 37. oldal	PDF  |  MathML
Témakör(ök):	Ábrázoló geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Csavarási inga: forgási rezgések   A forgási rezgések létrejötte 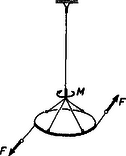  Ha egy testre ható erők eredője $0$, akkor a test haladó mozgás vonatkozásában egyensúlyban van. Ha ezenkívül az erők közös támadáspontban hatnak (vagy ha hatásvonalaik közös ponton mennek keresztül és ez a közös pont nem a végtelen távoli pont, azaz az erők nem párhuzamosak), akkor a test forgómozgás szempontjából is egyensúlyban van, tehát szögsebessége vagy $0$ vagy állandó. Két egyenlő nagyságú párhuzamos, ellentétes irányú erő esetén, vagy ha több erőt két olyan eredőben tudunk a vektori összegezés szabályai szerint egyesíteni, hogy a két eredő erőpárt alkot, akkor gyorsuló forgómozgás jön létre az ismert $M=I\beta$ alapösszefüggés szerint.       1. ábra   Ha a kísérletileg könnyen megvalósítható 1. ábra szerinti elrendezésre egyre növekvő nyomatékú erőpárral hatunk, a közvetlen tapasztalat azt mutatja, hogy a szögelfordulás arányos a forgatónyomatékkal és a szögelfordulás előjele megegyezik a forgatónyomaték előjelével; $\begin{array}{c}{\displaystyle M_1=D\phi \mathrm{,}}\end{array}$ ahol $M_1$ az alkalmazott forgatónyomaték, $\phi$ az elfordulás szöge, $D$ a direkciós nyomaték, mely az egyensúlyi helyzetből $\phi$ szöggel elforgatott testre ható $M_1$ forgatónyomaték nagyságának és $\phi$-nek a hányadosa. Dimenziója erő $\cdot$hosszúság, szám szerint azzal a forgatónyomatékkal egyezik meg, mely az illető elrendezésen $1$ radián szögelfordulást hoz létre. A $D$-nek MKS egysége N$\cdot$m. A külső forgatónyomaték meghatározott értéke mellett a korong egyensúlyi helyzetet foglal el. Mivel erőpárt csak erőpárral lehet kiegyensúlyozni, ezért az a forgatónyomaték, melyet a torziószál a felfüggesztett testre kifejt, a külső forgatónyomatékkal egyenlő nagyságú, de ellentétes előjelű: $M=-M_1$. Az előző összefüggés felhasználásával $\begin{array}{c}{\displaystyle M=-D\phi \mathrm{.}}\end{array}$ Ha a külső $M_1$ forgatónyomatékot megszüntetjük, ez a rugalmas elcsavarodásból származó $M$ nyomaték a testen forgómozgást hoz létre. Az így létrejövő mozgást forgási rezgésnek, a berendezést csavarási ingának nevezzük. A haladó és forgómozgás közötti formális analógia alapján is látszik, hogy a lineáris nyomatéki törvénynek akár az $M_1$, akár az $M$ nyomatékra felírt alakja kísértetiesen hasonlít a lineáris erőtörvény $F_1=Dx$ és $F=-Dx$ alakjához, ahol $F_1$ az alakváltoztató erő, melyet a rugóra helyezett testeknek az egyensúlyi helyzetből való $x$ kitérése esetén kell kifejtenünk, $F$ az $x$ kitérés esetén a rugótól a testre ható rugalmas visszatérítő erő, $D$ pedig jelenleg a direkciós erő (nem szerencsés a direkciós nyomatékkal való azonos jelölés, ezért az irodalomban a direkciós nyomatékot $D^{*}$-gal szokás jelölni), melynek dimenziója $\frac{\text{<span style="font-style: italic;">erő</span>}}{\text{<span style="font-style: italic;">hosszúság</span>}}$, MKS egysége $\frac{\text{N}}{\text{m}}$. A direkciós erő reciproka a $k$ rugóállandó, dimenziója $\frac{\text{<span style="font-style: italic;">hosszúság</span>}}{\text{<span style="font-style: italic;">erő</span>}}$, egysége $\frac{\text{m}}{\text{N}}$. A rugóra helyezett testet egyensúlyi helyzetéből kitérítve $F_1=-F$, és az $F_1$ megszüntetése után (a testet elengedve) $F$ által létrehozott mozgás a harmonikus rezgőmozgás.   Csavarási munka és a torziószál energiája   Forgómozgás során, ha a forgatónyomaték állandó, a végzett munkát $W=M\cdot \phi$ alapon számítjuk. Ha a nyomaték nem állandó, akkor a munkát $\begin{array}{c}{\displaystyle W=M_{\text{átl}}\cdot \phi }\end{array}$ összefüggés adja meg. Mivel a nyomaték a szögelfordulással arányos, mint lineárisan változó mennyiség átlagát, ebben az összefüggésben is az átlagnyomatékot a kezdő- és végérték számtani közepe adja: $\begin{array}{c}{\displaystyle W=M_{\text{átl}}\phi =\frac{M_{\text{max}}+M_{\text{min}}}{2}\left({\phi }_{\text{max}}-{\phi }_{\text{min}}\right)=\frac{D}{2}\left({\phi }_{\text{max}}+{\phi }_{\text{min}}\right)\left({\phi }_{\text{max}}-{\phi }_{\text{min}}\right)\mathrm{.}}\end{array}$ A szorzás elvégzése után $\begin{array}{c}{\displaystyle W=\frac{1}{2}D{\phi }_{\text{max}}^2-\frac{1}{2}D{\phi }_{\text{min}}^2\mathrm{.}}\end{array}$ Ha a csavarást az egyensúlyi helyzettől kezdjük, akkor $\begin{array}{c}{\displaystyle W=\frac{1}{2}D{\phi }_0^2\mathrm{,}}\end{array}$ ahol ${\phi }_0$ a maximális szögelfordulás. Az $M_0=D{\phi }_0$ összefüggés felhasználásával a munkára még a következő két kifejezést nyerjük: $\begin{array}{c}{\displaystyle W=\frac{M_0^2}{2D}=\frac{M_0{\phi }_0}{2}\mathrm{.}}\end{array}$ A munkának ezen három utóbbi képlete a torziószál energiáját is megadja az energiatétel értelmében.   A forgási rezgések jellemzése 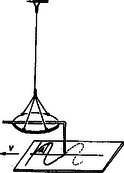      2. ábra   A közvetlen tapasztalat azt mutatja, hogy a létrejövő mozgás időben periodikus. Az ingára a 2. ábra szerint ecsetet helyezve, az egyenletesen mozgatott papírlapon kis szögelfordulás esetén szinuszos jel marad. Legyen a periódus $T$, az amplitúdó $A$. A kitérés időfüggvénye $y=A\text{sin}cT$. Kis szögek esetén $y$ arányos $\phi$-vel: $y=b\cdot \phi$, ahol $b$ az ecsetnek a forgástengelytől való távolsága. Ugyanígy $A=b\cdot {\phi }_0$, ahol ${\phi }_0$ a maximális kitérés szöge. Ezeknek az adatoknak a behelyettesítésével a szögelfordulás időtől való függése: $\begin{array}{c}{\displaystyle \phi ={\phi }_0\text{sin}ct\mathrm{.}}\end{array}$ A $c$ konstans meghatározása érdekében vegyük figyelembe azt, hogy $t=\frac{T}{4}$ idő elteltével $\phi ={\phi }_0\mathrm{.}$ Ez az értékpár tehát ki kell, hogy elégítse az alábbi egyenletet: $\begin{array}{c}{\displaystyle {\phi }_0={\phi }_0\text{sin}c\cdot \frac{T}{4}\mathrm{.}}\end{array}$ Ebből azonnal következik, hogy $c=\frac{2\pi }{T}=2\pi \cdot n$. Ez a mennyiség a körfrekvencia, jelentése a $2\pi$ idő alatt történő forgási rezgések száma. A későbbiekben a körfrekvenciát $\Omega$-val jelöljük. Ezzel a szögelfordulás időfüggvénye: $\begin{array}{c}{\displaystyle \phi ={\phi }_0\text{sin}\Omega t\mathrm{.}}\end{array}$ A $\Delta t$ időintervallumra vett átlagos szögsebességet $\frac{\Delta \phi }{\Delta t}$ adja. Mivel a szögelfordulás a mozgás kezdetétől számított $t+\Delta t$ időpillanatban ${\phi }_0\text{sin}\Omega \left(t+\Delta t\right)$, a $t$ időpillanatban ${\phi }_0\text{sin}\Omega t$, ezért az átlagos szögsebesség $\begin{array}{c}{\displaystyle \overline{\omega }=\frac{{\phi }_0\text{sin}\Omega \left(t+\Delta t\right)-{\phi }_0\text{sin}\Omega t}{\Delta t}}\end{array}$ Az összegezési tétel értelmében $\begin{array}{c}{\displaystyle \omega ={\phi }_0\frac{\text{sin}\Omega t\cdot \text{cos}\Omega \Delta t+\text{cos}\Omega t\text{sin}\Omega \Delta t-\text{sin}\Omega t}{\Delta t}\mathrm{.}}\end{array}$ Ez az átlagos szögsebesség annál jobban megközelíti a pillanatnyi szögsebességet, minél kisebb a $\Delta t$ időintervallum. De ekkor az $\Omega \Delta t$ szög is egyre kisebb lesz. Kis szögek esetén ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \text{cos}\Omega \Delta t\approx \mathrm{1,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \text{sin}\Omega \Delta t\approx \Omega \Delta t\mathrm{.}}\hfill \end{array}}$ Tehát az átlagos szögsebesség tetszőleges pontossággal megközelíti az $\begin{array}{c}{\displaystyle \omega ={\phi }_0\frac{\text{sin}\Omega t+\Omega \Delta t\text{cos}\Omega t-\text{sin}\Omega t}{\Delta t}={\phi }_0\Omega \text{cos}\Omega t}\end{array}$ értéket, hacsak $\Delta t$ elég kicsi, vagyis a pillanatnyi szögsebesség: $\begin{array}{c}{\displaystyle \omega ={\phi }_0\Omega \text{cos}\Omega t\mathrm{.}}\end{array}$ Ez az összefüggés minden forgási rezgésre igaz, e leírásból semmit nem tudunk meg a rezgések periódusáról. A közvetlen tapasztalat azt mutatja, hogy a rezgésidő a torziószál direkciós nyomatékától, valamint a rendszer tehetetlenségi nyomatékától függ. Ezeket az adatokat úgy tudjuk például az összefüggéseinkbe behozni, hogy energetikai megfontolásokat végzünk. A rendszerre érvényes az energiamegmaradás elve (külső nyomaték csupán a torziószál befogásánál hat, de ott a szögelfordulás $0$). A maximális szögelfordulásnál csak a torziószálnak van rugalmas energiája, egy tetszőleges helyzetben pedig a torziószálnak rugalmas és a testnek forgási energiája van: $\begin{array}{c}{\displaystyle \frac{1}{2}D{\phi }_0^2=\frac{1}{2}D{\phi }^2+\frac{1}{2}I{\omega }^2\mathrm{.}}\end{array}$ Ebből $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{D}{I}\left({\phi }_0^2-{\phi }^2\right)}\mathrm{.}}\end{array}$ A $\phi ={\phi }_0\text{sin}\Omega t$ helyettesítéssel $\begin{array}{c}{\displaystyle \omega ={\phi }_0\sqrt[]{\frac{D}{I}}\text{cos}\Omega t\mathrm{.}}\end{array}$ A szögsebességre kapott két összefüggés összevetéséből $\begin{array}{c}{\displaystyle \Omega =\sqrt[]{\frac{D}{I}}\mathrm{.}}\end{array}$ Ebből $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{I}{D}}\mathrm{.}}\end{array}$ Ha a pillanatnyi szöggyorsulást $\beta =\frac{\Delta \omega }{\Delta t}$ összefüggés alapján a $\Delta t$ időintervallumon belüli átlagos szöggyorsulásból az előbbiekhez hasonló módon számítjuk, akkor a $\begin{array}{c}{\displaystyle \beta =-{\phi }_0{\Omega }^2\text{sin}\Omega t}\end{array}$ összefüggéshez jutunk. Másrészt a forgómozgás alapegyenletéből $\begin{array}{c}{\displaystyle I\beta =-D{\phi }_0\text{sin}\Omega t\mathrm{,}}\end{array}$ ebből $\begin{array}{c}{\displaystyle \beta =-{\phi }_0\frac{D}{I}\text{sin}\Omega t\mathrm{.}}\end{array}$ A gyorsulásra kapott két kifejezés összevetéséből szintén a már megismert rezgésidő képlet adódik.   A fizikai inga 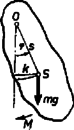  A fizikai inga olyan lengő rendszer, melynek minden pontja körpályán mozog. Legyen az inga tömege $m$, tehetetlenségi nyomatéka a $0$ ponton átmenő tengelyre $I$, súlypontjának a forgástengelytől mért távolsága $s$ (3. ábra).     3. ábra   Az ingát egyensúlyi helyzetéből $\phi$ szöggel kitérítve a visszatérítő nyomaték $\begin{array}{c}{\displaystyle M=-m\cdot g\cdot s\cdot \text{sin}\phi \mathrm{.}}\end{array}$ Ha $\phi$ kicsiny, akkor $\text{sin}\phi \approx \phi$, és figyelembe véve $\phi$ és $M$ ellentétes előjelét, lineáris nyomatéki törvényt kapunk: $\begin{array}{c}{\displaystyle M=-m\cdot g\cdot s\cdot \phi \mathrm{.}}\end{array}$ A létrejövő mozgás tehát forgási lengés $D=m\cdot g\cdot s$ direkciós nyomatékkal. A rezgésidő képletébe helyettesítve a fizikai inga lengésideje: $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{I}{mgs}}\mathrm{.}}\end{array}$ A fonálinga 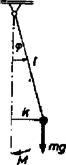    4. ábra   Fonálinga esetén (4. ábra) a nyomaték $M=-m\cdot g\cdot l\cdot \text{sin}\phi$. Az előbbi közelítéssel $M=-m\cdot g\cdot l\cdot \phi \mathrm{.}$ A $D=m\cdot g\cdot l$ és $I=m\cdot l^2$ összefüggésekkel a rezgésidőre $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{l}{g}}\text{<span style="font-weight: normal;font-style: normal;">adódik</span>}\mathrm{.}}\end{array}$ A csavarási inga egyik elterjedt alkalmazása az órákban az úgynevezett spirálrugós inga. Ezenkívül közismertek mind a fizika történetében, mind a modern technikában a torziószálas mérési berendezések.    Nagy László