Cím:	Megoldásvázlatok a 2009/2. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Darnai István
Füzet:	2009/március, 143 - 148. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Egy focicsapat $20$ fős keretében $3$ kapus, $6$ hátvéd, $7$ középpályás és $4$ csatár van. Az egyik mérkőzésen $1$ kapus, $4$ hátvéd, $3$ középpályás és $3$ csatár fog szerepelni. $a)$ Hányféleképpen állíthatja ki az edző a kezdőcsapatot?  (6 pont) $b)$ Az edző legalább $40$ pontot szeretne elérni az első $15$ összecsapáson. Hányféleképpen történhet ez meg, ha nem számít a megszerzett pontok sorrendje? (A győzelemért $3$, a döntetlenért $1$, a vereségért $0$ pont jár.)  (5 pont)   Megoldás. $a)$ 3 kapusból 1-et $\left(\genfrac{}{}{0ex}{}{3}{1}\right)=3$-féleképpen, 6 hátvédből 4-et $\left(\genfrac{}{}{0ex}{}{6}{4}\right)=15$-féleképpen, 7 középpályásból 3-at $\left(\genfrac{}{}{0ex}{}{7}{3}\right)=35$-féleképpen, 4 csatárból 3-at $\left(\genfrac{}{}{0ex}{}{4}{3}\right)=4$-féleképpen választhatunk. Összesen $3\cdot 15\cdot 35\cdot 4=6300$-féleképpen választhatjuk ki a csapatot. $b)$ A lehetséges eredményeket (győzelmek, döntetlenek, vereségek) és a pontszámok összegét a következő táblázatban látjuk:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle \text{győzelmek}}\hfill & \hfill {\displaystyle \text{döntetlenek}}\hfill & \hfill {\displaystyle \text{vereségek}}\hfill & \hfill {\displaystyle \text{pontszámok}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{összeg}}\hfill \\ \hfill {\displaystyle \text{15}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{45}}\hfill \\ \hfill {\displaystyle \text{14}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{43}}\hfill \\ \hfill {\displaystyle \text{14}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{42}}\hfill \\ \hfill {\displaystyle \text{13}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{41}}\hfill \\ \hfill {\displaystyle \text{13}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{40}}\hfill \\ \hline\end{array}}$   13 győzelem és 2 vereség 39 pontot ér, 13-nál kevesebb győzelem estén az elérhető maximális pontszám 39 (12 győzelem, 3 döntetlen, 0 vereség). Összesen 5-féleképpen lehet legalább 40 pontot elérni.   2. Egy osztály félévi matematikajegyei a következőképpen alakultak:   ${\displaystyle \begin{array}{|cccccc|}\hline {\displaystyle \text{osztályzat}}\hfill & \hfill {\displaystyle \text{1}}& \hfill {\displaystyle \text{2}}& \hfill {\displaystyle \text{3}}& \hfill {\displaystyle \text{4}}& \hfill {\displaystyle \text{5}}\\ {\displaystyle \text{gyakoriság}}\hfill & \hfill {\displaystyle \text{3}}& \hfill {\displaystyle \text{10}}& \hfill {\displaystyle \text{7}}& \hfill {\displaystyle \text{8}}& \hfill {\displaystyle }\\ \hline\end{array}}$   $a)$ Hányan kaptak jelest, ha tudjuk, hogy az osztályátlag 3,2 és 3,3 közé esik és az osztálylétszám páros?  (9 pont) $b)$ Határozzuk meg az osztályzatok móduszát és mediánját.  (4 pont)   Megoldás. Jelöljük az 5-ösök számát $x$-szel. Ekkor az átlag: $\begin{array}{c}{\displaystyle \overline{x}=\frac{3\cdot 1+10\cdot 2+7\cdot 3+8\cdot 4+x\cdot 5}{3+10+7+8+x}=\frac{76+5x}{28+x}\mathrm{.}}\end{array}$ A feladat szövege szerint: $3\mathrm{,}2<\overline{x}<3\mathrm{,}3$. ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 3\mathrm{,}2<\frac{76+5x}{28+x}\mathrm{,}}& {\displaystyle \text{amiből}}\hfill & {\displaystyle 7\mathrm{,}56<x\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{76+5x}{28+x}<3\mathrm{,}\mathrm{3,}}& {\displaystyle \text{amiből}}\hfill & {\displaystyle x<9\mathrm{,}65.}\hfill \end{array}}$ A kettő összevetésével: $7\mathrm{,}56<x<9\mathrm{,}65$. Mivel $x$ egész szám, ezért a lehetséges értékek: 8, 9, és tudjuk, hogy az osztálylétszám páros, így csak az $x=8$, lehet, és ekkor az osztálylétszám 36. Vagyis 8 tanuló kapott jeles osztályzatot. (Ekkor az átlag: $\overline{x}=\frac{116}{36}\approx 3\mathrm{,}22$.) $b)$ A módusz a leggyakrabban előforduló elem, azaz $m=2$. A medián a nagyság szerinti sorrend 18. és a 19. elemének számtani közepe, azaz $M=3$.   3. 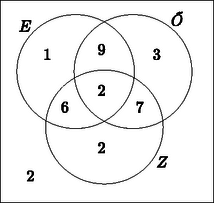Egy $36$ fős osztály ötéves érettségi találkozóján $32$-en jelentek meg. Az elmondottakból kiderült, hogy a három leggyakoribb nyári úti cél Erdély, a Zemplén és az Őrség volt. Erdélyben $18$-an nyaraltak, az Őrségben $21$-en, míg a Zemplént $17$-en választották. $11$-en voltak Erdélyben és az Őrségben, $9$-en az Őrségben és a Zemplénben, míg $8$-an Erdélyben és a Zemplénben. Ugyanannyian vannak azok, akik mindhárom helyen nyaraltak már, mint azok, akik a felsoroltak egyikén sem jártak. $a)$ Készítsünk Venn-diagrammot.  (9 pont) $b)$ Mekkora a valószínűsége, hogy egy tanulót véletlenszerűen kiválasztva legalább két helyen nyaralt már a felsoroltak közül?  (4 pont)   Megoldás. $a)$ Jelölje $E$ az Erdélyben, Ő az Őrségben, $Z$ a Zemplénben járt emberek halmazát. Ekkor: $\begin{array}{c}{\displaystyle |E|+|\text{<span style="font-style: italic;">Ő</span>}|+|Z|-|E\cap \text{<span style="font-style: italic;">Ő</span>}|-|E\cap Z|-|\text{<span style="font-style: italic;">Ő</span>}\cap Z|+|E\cap \text{<span style="font-style: italic;">Ő</span>}\cap Z|+|\overline{E\cup \text{<span style="font-style: italic;">Ő</span>}\cup Z}|=32.}\end{array}$ $18+21+17-11-8-9+x+x=32$, amiből $x=2$. Most már a Venn-diagramm elkészíthető.     $b)$ A legalább két helyen megfordulók száma: $\begin{array}{c}{\displaystyle 9+6+7+2=24.}\end{array}$ A keresett valószínűség: $\begin{array}{c}{\displaystyle P=\frac{24}{32}=\frac{3}{4}\mathrm{.}}\end{array}$   4. 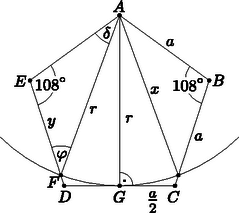Adott az $ABCDE$ 10 cm oldalhosszúságú szabályos ötszög, és az $A$ középpontú $k$ kör, amely érinti a $CD$ oldalt. Legyen a kör és $DE$ metszéspontja $F$. Mekkora az $EF$ távolság?  (14 pont)   Megoldás. Készítsünk ábrát. A koszinusztételből következik, hogy $x^2=a^2+a^2-2a^2\text{cos}{108}^{\circ }$, azaz $x^2=100+100-200\cdot \text{cos}{108}^{\circ }$, amiből $\begin{array}{c}{\displaystyle x\approx 16\mathrm{,}18.}\end{array}$     A Pitagorasz-tételből adódik, hogy $\begin{array}{c}{\displaystyle r^2=x^2-{\left(\frac{a}{2}\right)}^2\mathrm{,}}\end{array}$ amiből $r\approx 15\mathrm{,}39$. A szinusztétel alapján: $\begin{array}{c}{\displaystyle \frac{\text{sin}\phi }{a}=\frac{\text{sin}{108}^{\circ }}{r}\mathrm{,}\text{amiből}\text{sin}\phi =\frac{10\cdot \text{sin}{108}^{\circ }}{15\mathrm{,}39}\approx 0\mathrm{,}\mathrm{6180,}\text{azaz}\phi \approx 38\mathrm{,}{17}^{\circ }\mathrm{.}}\end{array}$ Ekkor $\delta ={180}^{\circ }-{108}^{\circ }-38\mathrm{,}{17}^{\circ }=33\mathrm{,}{83}^{\circ }$. Ismét a szinusztételt alkalmazzuk: $\begin{array}{c}{\displaystyle \frac{y}{\text{sin}\delta }=\frac{a}{\text{sin}\phi }\mathrm{,}\text{amiből}y=\frac{10\cdot \text{sin}33\mathrm{,}{83}^{\circ }}{\text{sin}38\mathrm{,}{17}^{\circ }}\approx 9\mathrm{,}01}\end{array}$ adódik. A keresett szakasz hossza kb. 9,01 cm.   II. 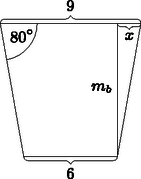rész   5. Agyagból szeretnénk csonkakúp alakú bögrét készíteni. Az alapkör belső átmérője 6 cm, a fedőköré 9 cm, a bögre oldala a vízszintessel ${80}^{\circ }$-os szöget zár be. $a)$ Hány deciliter folyadék fér a bögrébe?  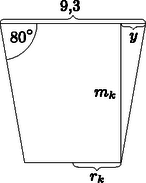(6 pont) A fedőkör külső átmérője 9,3 cm, a bögre fala mindenütt azonos vastagságú, az alja 4 mm vastag, a fülét 1,5 cm átmérőjű 15 cm magas egyenes körhengerből készítik. Az agyag sűrűsége ${\text{2,3 g/cm}}^3$. $b)$ Mennyi $10000$ bögre össztömege? (A tömeget kg-ban adjuk meg.)  (10 pont)   Megoldás. Készítsünk vázlatrajzot.     Mivel a bögre alapköreinek belső sugarai: $R_b=4\mathrm{,}5$, $r_b=3$, ezért $x=R_b-r_b=1\mathrm{,}5$. Felírható: $\begin{array}{c}{\displaystyle \text{tg}{80}^{\circ }=\frac{m_b}{x}=\frac{m_b}{1\mathrm{,}5}\mathrm{,}}\end{array}$ amiből a bögre belső magassága: $m_b=1\mathrm{,}5\cdot \text{tg}{80}^{\circ }\approx 8\mathrm{,}51$. Ekkor a bögre térfogata: $\begin{array}{c}{\displaystyle V_b=\frac{\left(R_b^2+R_b\cdot r_b+r_b^2\right)\cdot m_b\pi }{3}=\frac{\left(4\mathrm{,}{5}^2+4\mathrm{,}5\cdot 3+3^2\right)\cdot 8\mathrm{,}51\pi }{3}\approx 381.}\end{array}$ A bögre térfogata: kb. 381 cm${}^3\approx 0\mathrm{,}381$ dm${}^3=3\mathrm{,}81$ dl. $b)$ A külső adatokkal is elkészítjük az ábrát. A bögre nagyobb alapkörének külső sugara: $R_{\text{k}}=4\mathrm{,}65$.     Tudjuk, hogy $m_{\text{k}}=m_{\text{b}}+0\mathrm{,}4=8\mathrm{,}91$. Ekkor: $\begin{array}{c}{\displaystyle \text{tg}{80}^{\circ }=\frac{m_k}{y}=\frac{8\mathrm{,}91}{y}\mathrm{,}\text{amiből:}y=\frac{8\mathrm{,}91}{\text{tg}{80}^{\circ }}\approx 1\mathrm{,}57.}\end{array}$ Vagyis ${\displaystyle \begin{array}{c}\hfill {\displaystyle r_{\text{k}}=\frac{9\mathrm{,}3}{2}-1\mathrm{,}57=3\mathrm{,}08.}\hfill \\ \hfill {\displaystyle V_k=\frac{\left(R_k^2+R_k\cdot r_k+r_k^2\right)\cdot m_k\pi }{3}=\frac{\left(4\mathrm{,}{65}^2+4\mathrm{,}65\cdot 3\mathrm{,}08+3\mathrm{,}{08}^2\right)\cdot 8\mathrm{,}91\pi }{3}\approx 423\mathrm{,}9.}\hfill \end{array}}$ A fül térfogata: $V_{\text{fül}}=0\mathrm{,}{75}^2\cdot \pi \cdot 15\approx 26\mathrm{,}5$. A keresett térfogat: $V=V_{\text{k}}-V_{\text{b}}+V_{\text{fül}}=423\mathrm{,}9-381+26\mathrm{,}5=69\mathrm{,}4$. Az összes bögre térfogata: $10000\cdot 69\mathrm{,}4=694000$. Az összes bögre tömege: $m=694000\cdot 2\mathrm{,}3=1596200$. Vagyis a bögrék tömege kb. 1 596 200 g, ami kb. 1596 kg.   6. $a)$ Határozzuk meg $p$ értékét úgy, hogy a $9x^2+\left(p+16\right)x+2\mathrm{,}4p+1$ kifejezés teljes négyzet legyen.  (9 pont) $b)$ Számoljuk ki a $\begin{array}{c}{\displaystyle \underset{3}{\overset{5}{\int }}\left(9x^2+66x+121\right)dx}\end{array}$ kifejezés értékét.  (7 pont)   Megoldás. $a)$ A kifejezés pontosan akkor teljes négyzet, ha a két zérushely egyenlő, azaz a diszkrimináns 0. ${\displaystyle \begin{array}{c}\hfill {\displaystyle D=b^2-4ac={\left(p+16\right)}^2-4\cdot 9\cdot \left(2\mathrm{,}4p+1\right)=\mathrm{0,}\text{amiből}{p}^2-54\mathrm{,}4p+220=0.}\hfill \\ \hfill {\displaystyle p_{\mathrm{1,2}}=\frac{54\mathrm{,}4\pm \sqrt[]{2959\mathrm{,}36-880}}{2}=\frac{54\mathrm{,}4\pm 45\mathrm{,}6}{2}\mathrm{.}}\hfill \end{array}}$ A kifejezés teljes négyzet lesz, ha $p_1=50$, $p_2=4\mathrm{,}4$. $b)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle {\int }_3^{5}9x^2+66x+121dx={\left[3x^3+33x^2+121x\right]}_3^5=}\hfill \\ \hfill {\displaystyle }\end{array}}$ =3⋅53+33⋅52+121⋅5-(3⋅33+33⋅32+121⋅3)==1805-741=1064.   7. Egy $15$ millió lakosú országban egy cég vizsgálja a televízióműsorok nézettségét. $1500$ háztartás tévékészülékeit szerelték fel egy olyan berendezéssel, amely mindig rögzíti, hogy ki, mikor, melyik csatorna adását nézte. Az így figyelt $3200$ emberből ‐ akik nem- és korbeli összetétele a valóságot tükrözi ‐ tudják kiszámítani a nézettségi adatokat. A mintában szereplő $3200$ fő kor és nem szerinti eloszlását az alábbi táblázat mutatja.   ${\displaystyle \begin{array}{|ccccccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{0‐17}}\hfill & \hfill {\displaystyle \text{18‐27}}\hfill & \hfill {\displaystyle \text{28‐38}}\hfill & \hfill {\displaystyle \text{39‐49}}\hfill & \hfill {\displaystyle \text{50‐65}}\hfill & \hfill {\displaystyle \text{66‐}}\hfill \\ {\displaystyle \text{nők}}\hfill & \hfill {\displaystyle \text{540}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{240}}\hfill & \hfill {\displaystyle \text{220}}\hfill & \hfill {\displaystyle \text{290}}\hfill & \hfill {\displaystyle \text{110}}\hfill \\ {\displaystyle \text{férfiak}}\hfill & \hfill {\displaystyle \text{520}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{230}}\hfill & \hfill {\displaystyle \text{210}}\hfill & \hfill {\displaystyle \text{270}}\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$   $a)$ Töltsük ki a táblázat hiányzó adatait, ha tudjuk, hogy a $65$ évnél idősebb férfiak száma $375000$, és a vizsgált személyek között $100$-zal több a nő, mint a férfi.  (6 pont) $b)$ A szombat délelőtti gyerekműsort a minta $70$ tagja nézte. Hány nézőt jelent ez országosan?  (2 pont) $c)$ Ha ebben az időben 1,7 millióan tévéztek, akkor az éppen tévézők hány százaléka nézte a gyerekműsort?  (2 pont) $d)$ Egy műsor nézettsége jó, ha az éppen akkor tévézők legalább $25\%$-a azt nézi. Egy péntek esti vetélkedőműsort $504$-en néztek meg a mintából. Jó-e a műsor nézettsége, ha a lakosság $60\%$-a tévézett ekkor?  (6 pont)   Megoldás. $a)$ $\frac{375000}{15000000}\cdot 3200=80$, vagyis a mintában szereplő 65 évnél idősebb férfiak száma 80. Tudjuk, hogy $x+\left(x+100\right)=3200$, azaz $x=1550$. Vagyis 1550 férfi és 1650 nő van a mintában. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 1550-520-230-210-270-80}& {\displaystyle =\mathrm{240,}}\hfill \\ \hfill {\displaystyle 1650-540-240-220-290-110}& {\displaystyle =250.}\hfill \end{array}}$ Így megkaptuk a táblázat hiányzó adatait:   ${\displaystyle \begin{array}{|ccccccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{0‐17}}\hfill & \hfill {\displaystyle \text{18‐27}}\hfill & \hfill {\displaystyle \text{28‐38}}\hfill & \hfill {\displaystyle \text{39‐49}}\hfill & \hfill {\displaystyle \text{50‐65}}\hfill & \hfill {\displaystyle \text{66‐ }}\hfill \\ {\displaystyle \text{nők}}\hfill & \hfill {\displaystyle \text{540}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">250</span>}}\hfill & \hfill {\displaystyle \text{ 240}}\hfill & \hfill {\displaystyle \text{ 220}}\hfill & \hfill {\displaystyle \text{ 290}}\hfill & \hfill {\displaystyle \text{110 }}\hfill \\ {\displaystyle \text{férfiak}}\hfill & \hfill {\displaystyle \text{520}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">240</span>}}\hfill & \hfill {\displaystyle \text{ 230}}\hfill & \hfill {\displaystyle \text{ 210}}\hfill & \hfill {\displaystyle \text{ 270}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">80</span> }}\hfill \\ \hline\end{array}}$   $b)$ $\frac{70}{3200}\cdot 15000000=328125$. Vagyis ez országosan 328 125 nézőt jelent. $c)$ $\frac{328125}{1700000}\approx 0\mathrm{,}193=19\mathrm{,}3\%$. A tévézők kb. 19,3%-a nézte a gyerekműsort. $d)$ $\frac{504}{3200}\cdot 15000000=2362500$, és $15000000\cdot 0\mathrm{,}6=9000000$, továbbá $\begin{array}{c}{\displaystyle \frac{2362500}{9000000}=0\mathrm{,}2625=26\mathrm{,}25\%\mathrm{.}}\end{array}$ Vagyis a vizsgált műsornak jó a nézettsége.   8. Legyen $A$ halmaz a $\left]-\frac{9\pi }{4};2\pi \right]$, $B$ halmaz pedig a $\left[\frac{\pi }{6};\frac{11\pi }{2}\right[$ intervallum. Adjuk meg a $\begin{array}{c}{\displaystyle {\left(7\text{sin}x-2\right)}^2={\left(5\text{sin}x-6\right)}^2-4\left(\text{sin}x+2\right)}\end{array}$ egyenlet megoldásait az $A\backslash B$ és az $A\cap B$ halmazokon.  (16 pont)   Megoldás. A műveletek elvégzése és a $\text{sin}x=y$ helyettesítés után kapjuk: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 49y^2-28y+4=25y^2-60y+36-4y-\mathrm{8,}}\hfill \\ \hfill {\displaystyle 2y^2+3y-2=\mathrm{0,}}\hfill \\ \hfill {\displaystyle y_1=\frac{1}{2}\mathrm{,}{y}_2=-2.}\hfill \end{array}}$ $y_2$ nem megoldás, mert ($-1\le \text{sin}x\le 1$). Vagyis $\text{sin}x=\frac{1}{2}$, azaz $x_1=\frac{\pi }{6}+2k_1\pi$, $x_2=\frac{5\pi }{6}+2k_2\pi$, $k_1\mathrm{,}{k}_2\in \text{Z}$. ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle A\setminus B}& {\displaystyle =\left]-\frac{9\pi }{4};\frac{\pi }{6}\right]\mathrm{,}}\hfill & {\displaystyle \text{az intervallumba eső gyökök: }}\hfill & \hfill {\displaystyle -\frac{11\pi }{6}\text{ és }-\frac{7\pi }{6}\mathrm{.}}\\ \hfill {\displaystyle A\cap B}& {\displaystyle =\left[\frac{\pi }{6};2\pi \right]\mathrm{,}}\hfill & {\displaystyle \text{az intervallumba eső gyökök: }}\hfill & \hfill {\displaystyle \frac{\pi }{6}\text{ és }\frac{5\pi }{6}\mathrm{.}}\end{array}}$   9. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle x+\text{log}{}_{21}\left(3^x+1\right)=x\cdot \text{log}{}_{21}7+\text{log}{}_{21}756.}\end{array}$ (16 pont)   Megoldás. A logaritmus azonosságai alapján: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_{21}{21}^x+\text{log}{}_{21}\left(3^x+1\right)}& {\displaystyle =\text{log}{}_{21}{7}^x+\text{log}{}_{21}\mathrm{756,}}\hfill \\ \hfill {\displaystyle \text{log}{}_{21}{21}^x\left(3^x+1\right)}& {\displaystyle =\text{log}{}_{21}\left(7^x\cdot 756\right)\mathrm{.}}\hfill \end{array}}$ A logaritmusfüggvény szigorú monotonitása miatt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {21}^x\left(3^x+1\right)}& {\displaystyle =7^x\cdot \mathrm{756,}}\hfill \\ \hfill {\displaystyle 7^x{3}^x\left(3^x+1\right)}& {\displaystyle =7^x\cdot 756.}\hfill \end{array}}$ Mivel $7^x\ne 0$, ezért oszthatunk vele: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 3^x\left(3^x+1\right)=\mathrm{756,}}\hfill \\ \hfill {\displaystyle {\left(3^x\right)}^2+3^x-756=\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(3^x\right)}_{\mathrm{1,2}}=\frac{-1\pm \sqrt[]{1+4\cdot 756}}{2}=\frac{-1\pm 55}{2}\mathrm{.}}\hfill \\ \hfill {\displaystyle y_1=\mathrm{27,}{y}_2=-28.}\hfill \end{array}}$ A $-28$ nem megoldás, mert $3^x>0$. Vagyis $3^x=3^3$, azaz: $x=3$. Ez minden feltételnek megfelel, így valóban megoldása az egyenletnek.