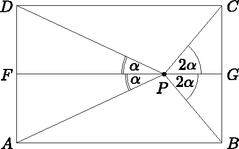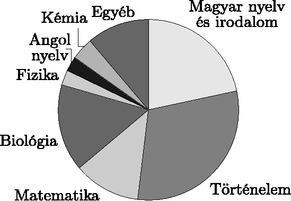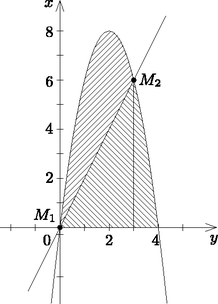Cím:	Megoldásvázlatok a 2006/9. sz. emelt szintű gyakorló feladatokhoz
Szerző(k):	Juhászné Kunstár Mária ,  Marczis György ,  Mihály Mária ,  Székely András ,  Tóth István
Füzet:	2007/január, 6 - 11. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. $a)$ Egy $1600$ kötetes iskolai könyvtár magyar és angol nyelvű könyvekből áll. Magyar nyelvű a könyvek $p\%$-a. Ezen könyvek $p\%$-a angol fordításban is megtalálható a könyvtárban. Az eredetileg angol nyelven írt könyvek száma $64$. Határozza meg a magyar és az angol nyelvű könyvek arányát. $b)$ Év végén a beszerzéseket követő felújítás során az összes könyvet egyforma dobozokba pakoljuk. Ha dobozonként $25$ könyvet teszünk, akkor $17$ könyv kimarad, ha $27$ könyvet csomagolunk, akkor négy doboz üresen marad és az utolsónak megrakott dobozba is fér még $5$ könyv. Hány dobozunk volt a pakoláshoz? Hány könyvvel gyarapodott a könyvtár állománya az év végére?   Megoldás. $a)$ Magyar nyelvű könyv $1600\cdot \frac{p}{100}$, abból angolra fordított $1600\cdot \frac{p^2}{10000}$. Ha ehhez hozzávesszük az eredetileg angol nyelven írottakat, akkor a teljes angol nyelvű állományt kapjuk, ami $\left(100-p\right)\%$-nak felel meg. Így az egyenlet: $\begin{array}{c}{\displaystyle 1600\cdot \frac{p^2}{10000}+64=1600\cdot \frac{100-p}{100}\mathrm{,}}\end{array}$ amiből adódik, hogy $p^2+100p-9600=0$. Ennek egyetlen pozitív megoldása a $p=60$. Magyar nyelvű könyv 960, angol nyelvű 640 db van, így az arányuk $3:2$. $b)$ A dobozok számát $d$-vel jelölve, a könyvek számát felírhatjuk $25d+17$, illetve $27\left(d-5\right)+22$ alakban. A megfelelő egyenlőség felírásából $d=65$ adódik. Visszahelyettesítve 1642 könyvet kapunk, vagyis 42 könyvvel gyarapodott az állomány.   2. Az $x^2+y^2=25$ egyenletű körhöz a $3$ abszcisszájú pontjaiban érintőket rajzolunk. $a)$ Írjuk fel az érintők egyenletét. $b)$ Határozzuk meg az érintők hajlásszögét.   Megoldás. $a)$ Az érintési pontok koordinátái: $P_1\left(3;4\right)$, $P_2\left(3;-4\right)$. A kör középpontja az origó. A 3 abszcisszájú pontokban rajzolt érintők normálvektorai: $\left(3;4\right)$, $\left(3;-4\right)$. Az érintők egyenlete: $3x+4y=25$, $3x-4y=25$. $b)$ A hajlásszög megegyezik a normálvektorok hajlásszögével, tompaszög esetén a kiegészítőszögével: $|\overrightarrow{n_e}|=|\overrightarrow{n_f}|=5$. A vektorok skaláris szorzata: $\begin{array}{c}{\displaystyle \overrightarrow{n_e}\cdot \overrightarrow{n_f}=3\cdot 3+4\cdot \left(-4\right)=9-16=-\mathrm{7,}\overrightarrow{n_e}\cdot \overrightarrow{n_f}=|\overrightarrow{n_e}|\cdot |\overrightarrow{n_f}|\cdot \text{cos}\alpha \mathrm{,}\text{cos}\alpha =-\frac{7}{25}\mathrm{.}}\end{array}$ (Az $\alpha$ az egyenesek iránytangensének ismeretében is meghatározható.) $\alpha \approx 106\mathrm{,}{26}^{\circ }\approx 1\mathrm{,}85$ radián. Mivel ez tompaszög, azért az egyenesek hajlásszöge ${\alpha }_{e\mathrm{,}f}\approx 73\mathrm{,}{74}^{\circ }\approx 1\mathrm{,}29$ radián.   3. Mely valós számok teljesítik a $\begin{array}{c}{\displaystyle \text{log}{}_{4-5x}\left(4x^2+1-4x\right)+\text{log}{}_{2x-1}\left(13x-4-10x^2\right)=4}\end{array}$ egyenlőséget?   Megoldás. Figyelembe véve, hogy $4x^2+1-4x={\left(2x-1\right)}^2$ és $13x-4-10x^2=\left(4-5x\right)\left(2x-1\right)$, az értelmezési tartomány a következőképpen alakul: $4-5x>$0 és $4-5x\ne 1$ és $2x-1>$0 és $2x-1\ne 1$, amiből $\frac{1}{2}<x<\frac{4}{5}$ és $x\ne \frac{3}{5}$. A logaritmus azonosságainak felhasználásával, új változó, az $y=\text{log}{}_{4-5x}\left(2x-1\right)$ bevezetésével és felismerve, hogy $\text{log}{}_{4-5x}\left(2x-1\right)=\frac{1}{\text{log}{}_{2x-1}\left(4-5x\right)}$ kapjuk a következő, másodfokúra vezethető egyenletet: $2y+\frac{1}{y}=3$. Megoldásai: $y_1=1$ és $y_2=\frac{1}{2}$. Az elsőből: $\text{log}{}_{4-5x}\left(2x-1\right)=1$, azaz $2x-1=4-5x$, amiből $x_1=\frac{5}{7}$ adódik, és ez megoldás. A másodikból $\text{log}{}_{4-5x}\left(2x-1\right)=\frac{1}{2}$, azaz $2x-1=\sqrt[]{4-5x}$, amiből: $x_2=\frac{3}{4}$ és $x_3=-1$. Ez utóbbi nem megoldása sem a fenti, sem az eredeti egyenletnek. Összegezve: az egyenlőséget két valós szám teljesíti. A megoldások: $\frac{3}{4}$ és $\frac{5}{7}$.   4. Egy öttagú családban a szülők életkorának összege $80$ év, közülük az apa az idősebb. Három fiuk életkora prímszám differenciájú számtani sorozat három egymást követő eleme, összegük $30$. Hány évesek a család tagjai, ha az apa két évvel ezelőtt háromszor annyi idős volt, mint a legidősebb fiú, akinek a születésekor az anya $20$ évesnél idősebb volt?   Megoldás. Legyen az apa életkora $x$ év. Az anya életkora így $80-x$. Mivel a férj idősebb a feleségnél, $x\ge 41$. A feltétel alapján a fiúk életkora $10-p$, 10, $10+p$, ahol $p$ prímszám. Két évvel ezelőtt az apa $x-2$, legidősebb fia $8+p$ éves volt. Így $x-2=3\left(8+p\right)$, vagyis $x=26+3p$, azaz $26+3p\ge 41$. Ebből $p\ge 5$. Az anya és legidősebb fia életkorának különbsége: $\left(80-x\right)-\left(10+p\right)>20$, amiből $x<50-p$. Mivel $x=26+3p$, azért $26+3p<50-p$, azaz $p<6$. Ezek alapján $5\le p<6$, vagyis $p=5$. Az apa 41, az anya 39 éves, a fiaik életkora: 5; 10; 15.   II. rész   5. Egy dobozban nyolc, tapintásra teljesen egyforma golyó van. Egyikükre a $3$, másik kettőre a $2$, ötre pedig az $1$ számot írták. Valaki a golyók közül hármat kivesz, majd összeadja a golyókról leolvasott számokat. $a)$ Milyen eredményeket kaphat így? $b)$ Mennyi az egyes eredmények valószínűsége?   Megoldás. $a)$ A lehetséges összegek: $3=1+1+1$;  $4=1+1+2$;  $5=1+1+3=1+2+2$;  $6=1+2+3$;  $7=2+2+3$. $b)$ Az összes golyóhármas száma $C_8^3=\left(\genfrac{}{}{0ex}{}{8}{3}\right)=56$ (8 golyó közül 3-at kell sorrend nélkül kiválasztani). A 3 összeg kedvező eseteinek száma $C_5^3=\left(\genfrac{}{}{0ex}{}{5}{3}\right)=10$ (az 5 db 1-gyel jelölt golyó közül 3-at kell sorrend nélkül kiválasztani), így ennek a valószínűsége $P_3=\frac{C_5^3}{C_8^3}=\frac{10}{56}\approx 0\mathrm{,}1786$. A 4 összeghez 2 db 1-gyel jelölt mellé 1 db 2-vel jelöltet kell választani, a kedvező esetek száma $C_5^2\cdot C_2^1=\left(\genfrac{}{}{0ex}{}{5}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{2}{1}\right)=10\cdot 2=20$, ezért $P_4=\frac{20}{56}\approx 0\mathrm{,}3571$. Az 5 összeget két különböző módon is megkaphatjuk, ezt láthattuk az $a)$ kérdésre adott válasznál, ezért a kedvező esetek száma: $C{}_5^2\cdot C{}_1^1+C{}_5^1\cdot C{}_2^2=10\cdot 1+5\cdot 1=15$, vagyis $P_5=\frac{15}{56}\approx 0\mathrm{,}2679$. A 6 összegre: $C_5^1\cdot C_2^1\cdot C_1^1=5\cdot 2\cdot 1=10$, vagyis $P_6=\frac{10}{56}\approx 0\mathrm{,}1786$. A 7 összegre: $C_2^2\cdot C_1^1=1\cdot 1=1$, vagyis $P_7=\frac{1}{56}\approx 0\mathrm{,}0179$.   6. Egy téglalap két oldala $6\text{cm}$ és $4\text{cm}$ hosszú. Hol helyezkedik el a hosszabbik középvonalon az a $P$ pont, amelyből az egyik $4\text{cm}$ hosszú oldal kétszer akkora szögben látszik, mint a másik $4\text{cm}$-es oldal?   Megoldás. A középvonal egyenese szimmetriatengely, ezért az ábrán az azonosan jelölt szögek egyenlők. Legyen $FP=x$, ekkor $PG=6-x$.     Az $AFP$ derékszögű háromszögben $\text{tg}\alpha =\frac{2}{x}$, a $BGP$ derékszögű háromszögben $\text{tg}2\alpha =\frac{2}{6-x}$. A $\text{tg}2\alpha =\frac{2\text{tg}\alpha }{1-{\text{tg}}^2\alpha }$ azonosságba helyettesítsük be az előbbieket, és rendezzük az egyenletet: $\begin{array}{c}{\displaystyle \frac{2}{6-x}=\frac{2\cdot \frac{2}{x}}{1-{\left(\frac{2}{x}\right)}^2}\mathrm{,}\text{ahonnan}3x^2-12x-4=\mathrm{0,}{x}_1=2+\frac{4\sqrt[]{3}}{3}\approx 4\mathrm{,}309;x_2<0.}\end{array}$ Két adott tulajdonságú pont van a hosszabbik középvonalon, a középpontra szimmetrikusan, attól $\frac{4\sqrt[]{3}}{3}-1\approx 1\mathrm{,}309$ egységnyire.   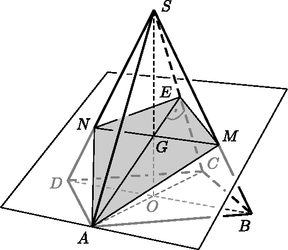7. Egy négyoldalú egyenes gúla alaplapja $a$ oldalú négyzet és minden oldaléle ${30}^{\circ }$-os szöget zár be a gúla magasságával. Mekkora területű síkidomban metszi a gúlát egy olyan sík, amelyik átmegy a gúla alaplapjának egyik csúcsán és merőleges a szemközti oldalélre?     Megoldás. Tekintsük az $SABCD$ gúla $A$ csúcsára illeszkedő, $SC$-re merőleges síkot. Ez $SC$-t $E$ pontban, $SB$-t $M$-ben, $SD$-t $N$-ben, a gúla $SO$ magasságát pedig $G$ pontban metszi.     A sík merőlegessége miatt $AE\perp SC$, a gúla szimmetrikus voltából $NM\parallel DB$ következik. $ASO\sphericalangle =CSO\sphericalangle ={30}^{\circ }$, $CSO\sphericalangle =EAC\sphericalangle$, mert merőleges szárú szögek, így $2AO=AS=SC=a\sqrt[]{2}$, az $ACS$ háromszög szabályos, magassága az $AE$, és így $AE=a\sqrt[]{2}\frac{\sqrt[]{3}}{2}=\frac{a\sqrt[]{6}}{2}$. Az $ACS$ szabályos háromszögben $G$ magasságpont és súlypont is, tehát a $G$ pont az $SBD$ szabályos háromszögben súlypont lesz, harmadolja $SO$-t, így a párhuzamos szelők tétele miatt $MN=\frac{2}{3}DB=\frac{2}{3}a\sqrt[]{2}$. Az $AMEN$ síknégyszög 2‐2 szomszédos oldala egyenlő a gúla $ACS$ síkra vonatkozó szimmetriája miatt, ezért e négyszög deltoid, területe az átlók szorzatának fele: $\begin{array}{c}{\displaystyle T=\frac{AE\cdot MN}{2}=\frac{\frac{a\sqrt[]{6}}{2}\cdot \frac{2a\sqrt[]{2}}{3}}{2}=\frac{a^2\sqrt[]{3}}{3}\mathrm{.}}\end{array}$   8. A $2006$-os május‐júniusi érettségi vizsgán az emelt szintű írásbeli dolgozatok javításával kapcsolatban az összes vizsgatárgynál tett tanulói észrevételek (beadványok) megoszlását látjuk az alábbi táblázatban. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccc|}\hline {\displaystyle \text{Tantárgy}}\hfill & \hfill {\displaystyle \text{Beadványok száma}}\hfill & \hfill {\displaystyle \text{Írásbeli dolgozatok száma}}\hfill \\ {\displaystyle \text{Magyar nyelv és irodalom}}\hfill & \hfill {\displaystyle \text{1187}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>6251}}\hfill \\ {\displaystyle \text{Történelem}}\hfill & \hfill {\displaystyle \text{1660}}\hfill & \hfill {\displaystyle \text{11617}}\hfill \\ {\displaystyle \text{Matematika}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>657}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>6408}}\hfill \\ {\displaystyle \text{Biológia}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>855}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>5530}}\hfill \\ {\displaystyle \text{Fizika}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>149}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>1745}}\hfill \\ {\displaystyle \text{Angol nyelv}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>145}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>3956}}\hfill \\ {\displaystyle \text{Kémia}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>218}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>1814}}\hfill \\ {\displaystyle \text{Egyéb}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>614}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>8700}}\hfill \\ {\displaystyle \text{Összesen}}\hfill & \hfill {\displaystyle \text{5485}}\hfill & \hfill {\displaystyle \text{46021}}\hfill \\ \hline\end{array}}}\end{array}$ $a)$ Ábrázoljuk kördiagrammal a beadványok megoszlását. $b)$ Mennyi a terjedelme a hét tantárgynál a beadványok, illetve az írásbeli dolgozatok számának? $c)$ Határozzuk meg a beadványok számának a szórását a hét tantárgy figyelembevételével. $d)$ Melyik tantárgynál ,,reklamáltak'' leginkább az érettségizők? $e)$ Számítsuk ki a hét tantárgyhoz tartozó beadványok számának részarányát százalékban (vagyis a beadványok számát az írásbeli dolgozatok számához képest), majd határozzuk meg az összesített részaránytól való átlagos abszolút eltérést.     Megoldás. $a)$     $b)$ A beadványok tantárgyankénti számának terjedelme: $1660-145=1515$. Az írásbeli dolgozatok tantárgyankénti számának terjedelme: $11617-1745=9872$. $c)$ A beadványok számának szórása: $\begin{array}{c}{\displaystyle D_7\left(x\right)=\sqrt[]{\frac{Q}{7}}\approx \mathrm{538,}}\end{array}$ ahol ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle Q}& {\displaystyle =}\hfill & {\displaystyle {\left(1187-\overline{a}\right)}^2+{\left(1660-\overline{a}\right)}^2+{\left(657-\overline{a}\right)}^2+{\left(855-\overline{a}\right)}^2+{\left(149-\overline{a}\right)}^2+}\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle +{\left(145-\overline{a}\right)}^2+{\left(218-\overline{a}\right)}^2\mathrm{,}\text{ahol <math xmlns="http://www.w3.org/1998/Math/MathML"><mover accent="true"><mrow><mi>a</mi></mrow><mo>¯</mo></mover></math> a hét adat számtani közepe: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover accent="true"><mrow><mi>a</mi></mrow><mo>¯</mo></mover><mo>≈</mo><mn>696</mn></math>.}}\hfill \end{array}}$ $d)$ Magyar nyelv és irodalomnál, itt a legnagyobb a részarány (18,99%). $e)$ Az összesített részarány az összes beadvány száma az összes dolgozat számához képest: 11,92. A százalékban kifejezett részarányok átlagos abszolút eltérése: ${\displaystyle \begin{array}{c}\hfill {\displaystyle S_7\left(11\mathrm{,}92\right)=\frac{b}{7}\approx 3\mathrm{,}\mathrm{77,}\text{ahol}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle b}& \hfill {\displaystyle =}\hfill & {\displaystyle |18\mathrm{,}99-11\mathrm{,}92|+|14\mathrm{,}29-11\mathrm{,}92|+|10\mathrm{,}25-11\mathrm{,}92|+|15\mathrm{,}46-11\mathrm{,}92|+}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle +|8\mathrm{,}54-11\mathrm{,}92|+|3\mathrm{,}67-11\mathrm{,}92|+|12\mathrm{,}02-11\mathrm{,}92|\mathrm{.}}\hfill \end{array}}}\hfill \end{array}}$   9. Az $y=a{x}^2+bx+c$ parabola átmegy az origón, és az $E\left(3;6\right)$ pontjához húzott érintő meredeksége $-4$. $a)$ Írjuk fel a parabola egyenletét. $b)$ Adjuk meg a parabola fentebb megadott érintőjének egyenletét. $c)$ Milyen arányban osztja az $y=2x$ egyenes a parabola és az $x$ tengely által közrefogott síkidom területét?   Megoldás. $a)$ A parabola egyenlete: $y=a{x}^2+bx+c$. $O\left(0;0\right)$ rajta van a parabolán, ezért $c=0$. $E\left(3;6\right)$ is rajta van a parabolán, ezért $6=9a+3b+c$, vagyis $\begin{array}{c}{\displaystyle 2=3a+b\mathrm{.}}\end{array}$ (1) Az érintő meredekségét a derivált adott helyen vett helyettesítési értéke adja meg: $y\text{'}=2ax+b$. Mivel $m_E=-4$, azért $\begin{array}{c}{\displaystyle 6a+b=-4.}\end{array}$ (2) Az (1), (2) egyenletrendszer megoldása: $a=-2$ és $b=8$. Így a szóban forgó parabola egyenlete: $y=-2x^2+8x$. $b)$ Az érintő átmegy az $E\left(3;6\right)$ ponton és a meredeksége $m=-4$, így az $y-y_0=m\left(x-x_0\right)$ képlet alapján az egyenlete: $y=-4x+18$. $c)$ Az $y=-2x^2+8x$ egyenletű parabola zérushelyeit szorzattá alakítással kapjuk: $x_1=0$ és $x_2=4$. Az $y=2x$ egyenes az $y=-2x^2+8x$ egyenletű parabolát azokban a pontokban metszi, amelyek koordinátái az egyenleteikből alkotott egyenletrendszer megoldásai: $M_1\left(0;0\right)$ és $M_2\left(3;6\right)$.     A ,,középső'' síkidom, a háromszög területe: $\begin{array}{c}{\displaystyle T_2=\frac{3\cdot 6}{2}=9.}\end{array}$ A ,,felső'' síkidom területe a parabola ,,alatti'' terület és $T_2$ különbsége (Newton‐Leibniz tétel alapján): $\begin{array}{c}{\displaystyle T_1=\underset{0}{\overset{3}{\int }}\left(-2x^2+8x\right)dx-9={\left[-\frac{2}{3}{x}^3+4x^2\right]}_0^3-9=-18+36-9=9.}\end{array}$ A ,,jobb oldali'' síkidom területe a parabola ,,alatti'' terület: $\begin{array}{c}{\displaystyle T_3=\underset{3}{\overset{4}{\int }}\left(-2x^2+8x\right)dx={\left[-\frac{2}{3}{x}^3+4x^2\right]}_3^4=-\frac{128}{3}+64-\left(-18+36\right)=\frac{10}{3}\mathrm{.}}\end{array}$ A keresett arány: $\begin{array}{c}{\displaystyle \frac{T_1}{T_2+T_3}=\frac{9}{9+\frac{10}{3}}=\frac{27}{37}\mathrm{.}}\end{array}$