Kezdőlap


Cím:	A 47. Nemzetközi Matematikai Diákolinpia feladatainak megoldásai
Szerző(k):	Erdélyi Márton , Jankó Zsuzsanna , Kis Gergely , Nagy Csaba , Paulin Roland , Tomon István
Füzet:	2006/október, 386 - 393. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	2006/szeptember: Beszámoló a 47. Nemzetközi Matematikai Diákolimpiáról Feladatok: 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 11. feladata, 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 12. feladata, 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 13. feladata, 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 21. feladata, 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 22. feladata, 2006/szeptember: 2006. évi Nemzetközi Matematika Diákolimpia 23. feladata Feladatok megoldásai: 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 13. feladata, 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 11. feladata, 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 12. feladata, 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 21. feladata, 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 22. feladata, 2006/október: 2006. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

1. Az

A B C

háromszög beírt körének középpontja legyen

I

. A háromszög

P

belső pontja kielégíti a

\begin{matrix} P B A ∢ + P C A ∢ = P B C ∢ + P C B ∢ \end{matrix}

egyenlőséget. Bizonyítsuk be, hogy

A P \geq A I

, és egyenlőség akkor és csak akkor áll fenn, ha

P = I

Nagy Csaba megoldása. Legyenek az

A B C

háromszög szögei

α

β

γ

. A feltétel szerint egyenlő szögösszegek közös értékét jelölje

φ

. Ekkor

2 φ = β + γ

, azaz

φ = \frac{β + γ}{2}

\begin{matrix} B P C ∢ = 180^{\circ} - φ = 180^{\circ} - \frac{β}{2} - \frac{γ}{2} = B I C ∢, \end{matrix}

és mivel a

B C

egyenes nem választja el a

P

és

I

pontokat, innen következik, hogy

B I P C

húrnégyszög,

P

tehát rajta van a

B I C

körülírt körén.
Legyen

A I

és az

A B C

körülírt körének másik metszéspontja

Q

(1. ábra). Ismeretes, hogy

Q

felezi az őt tartalmazó

B C

ívet, ezért

Q B = Q C

. Másfelől

Q C I ∢ = \frac{γ}{2} + \frac{α}{2} = Q I C ∢

, mert az

A I C

háromszög külső szöge, ezért

Q C = Q I

. A fenti

B I P C

húrnégyszög körülírt körének a középpontja tehát a

Q

, és így

Q I = Q P

1. ábra

A P Q

háromszögben a háromszög-egyenlőtlenség miatt

\begin{matrix} A P + P Q \geq A Q = A I + I Q, \end{matrix}

azaz valóban fennáll, hogy

A P \geq A I

. Egyenlőség pontosan akkor teljesül, ha

P

A Q

szakasz pontja, azaz

P = I

2. Legyen

P

egy szabályos

2006

-szög.

P

egy átlóját jónak nevezzük, ha a végpontjai

P

határát két olyan részre bontják, amelyek mindegyike

P

páratlan sok oldalát tartalmazza. Az oldalakat szintén jónak nevezzük.
Tegyük fel, hogy

P

-t háromszögekre bontottuk

2003

olyan átlóval, amelyek közül semelyik kettőnek nincs közös pontja

P

belsejében. Határozzuk meg az ilyen felbontásokban előforduló egyenlőszárú, két jó oldallal rendelkező háromszögek számának maximumát.

Jankó Zsuzsanna megoldása. A 2003 egymást nem metsző átló a

P

sokszöget 2004 háromszögre bontja, amelyek csúcsai a

P

csúcsai. Nevezzünk egy ilyen háromszöget jónak, ha két oldala jó és egyenlő szárú.
Legyen

A B

a sokszög egy átlója vagy oldala, és jelöljük

n

-nel az

A, B

csúcsokat összekötő, sokszögoldalakból álló két töröttvonal közül a rövidebbik (nem hosszabbik) oldalainak a számát (

1 \leq n \leq 1003

). A megrajzolt átlók azt a

P_{1}

sokszöget is háromszögekre bontják, amelyet az

n

oldalszakaszból álló töröttvonal és az

A B

szakasz határol. (Ha

n = 1

, azaz

A B

P

egy oldala, akkor a

P_{1}

sokszög szakasszá fajul, a háromszögek száma 0.) Jelöljük

f (n)

-nel, hogy ezt a sokszöget az

A B

-t és egymást nem metsző átlók megrajzolásával (az eredeti felbontás átlói közül

(n - 2)

ilyen van) háromszögekre bontva legfeljebb hány jó háromszög jöhet létre. Az

n

-re vonatkozó teljes indukcióval bebizonyítjuk, hogy

f (n) \leq ⌊ \frac{n}{2} ⌋

.
Ha

n = 1

, akkor

A

és

B

szomszédos csúcsok

P

-ben, egyetlen háromszög sem jön létre

P_{1}

-ben, így jó sem,

f (1) = 0 = ⌊ \frac{1}{2} ⌋

. Ha

n = 2

, akkor

A

és

B

másodszomszédos csúcsok

P

-ben, a létrejövő egyetlen háromszög jó,

f (2) = 1

, az állítás igaz. Legyen most

n > 2

és tegyük föl, hogy

f (i) \leq ⌊ \frac{i}{2} ⌋

, ha

2 \leq i < n

. Tekintsük a

P_{1}

sokszögnek azt a felbontását, amelynek során

f (n)

jó háromszöget kapunk. Ebben a felbontásban a létrejövő háromszögek egyikének oldala az

A B

, legyen e háromszög harmadik csúcsa

C

(2. ábra). Ha az

A C

oldalt

i

, a

B C

-t pedig

j

hosszúságú töröttvonal köti össze, akkor

1 \leq i, j < n

és

i + j = n

. Ekkor nyilván

\begin{matrix} f (n) = {\begin{matrix} f (i) + f (j), & ha azA B Cnem jó, \\ f (i) + f (j) + 1, & ha azA B Cjó. \end{matrix} \end{matrix}

Az első esetben az indukciós föltevést tagonként alkalmazva és felhasználva, hogy

⌊ x ⌋ + ⌊ y ⌋ \leq ⌊ x + y ⌋

\begin{matrix} f (n) = f (i) + f (j) \leq ⌊ \frac{i}{2} ⌋ + ⌊ \frac{j}{2} ⌋ \leq ⌊ \frac{i + j}{2} ⌋ = ⌊ \frac{n}{2} ⌋ . \end{matrix}

Nézzük meg, hogyan lehetséges a második eset. A

P_{1}

megválasztása miatt

A B

a leghosszabb a

P_{1}

csúcsait összekötő szakaszok közül, így az

A B C

háromszögben is

A B

a leghosszabb oldal. Ez a háromszög tehát csak úgy lehet egyenlő szárú, ha

A C = C B

. Egy egyenlő szárú háromszögnek vagy mindkét szára jó, vagy egyik sem az (a háromszögnek és

P

-nek közös szimmetriatengelye van), így ha az egyenlő szárú

A B C

háromszög jó, akkor az

A C

és

B C

szárak a jó oldalai. Ekkor

i

és

j

egyenlő páratlan számok, azaz

n = 4 k + 2

alakú. Az indukciós feltevés szerint

f (\frac{n}{2}) \leq [\frac{n}{2}]

és így

\begin{matrix} f (n) = f (\frac{n}{2}) + f (\frac{n}{2}) + 1 \leq 2 ⌊ \frac{n}{4} ⌋ + 1 = 2 \cdot k + 1 = ⌊ \frac{n}{2} ⌋, \end{matrix}

az indukciós lépést igazoltuk.

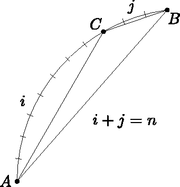2. ábra

Tekintsük ezek után a

P

sokszög megrajzolt átlóit. Ha van köztük olyan, amelyik áthalad a sokszög középpontján, akkor a jó háromszögek maximális száma

\begin{matrix} f (1003) + f (1003) \leq 2 \cdot ⌊ \frac{1003}{2} ⌋ = 1002. \end{matrix}

Ha ilyen átló nincsen, akkor tekintsük a felbontásban szereplő háromszögek közül azt, amelyik a belsejében tartalmazza a sokszög középpontját. Ennek bármely két csúcsát a

P

félkerületénél rövidebb töröttvonal köti össze, álljanak ezek rendre

a, b, c

szakaszból. (

a + b + c = 2006

.) Ha ez a háromszög jó, akkor

a

b

és

c

közül kettő páratlan, a felbontás összesen legfeljebb

\begin{matrix} 1 + ⌊ \frac{a}{2} ⌋ + ⌊ \frac{b}{2} ⌋ + ⌊ \frac{c}{2} ⌋ = 1 + \frac{a + b + c}{2} - 1 = 1003, \end{matrix}

ha pedig nem jó, akkor legfeljebb

\begin{matrix} ⌊ \frac{a}{2} ⌋ + ⌊ \frac{b}{2} ⌋ + ⌊ \frac{c}{2} ⌋ \leq ⌊ \frac{a + b + c}{2} ⌋ = 1003 \end{matrix}

jó háromszöget tartalmaz.
A kapott felső korlát éles,

1003

jó háromszög jön létre, ha a másodszomszédos csúcsokat kötjük össze, a ,,belső''

1003

oldalú sokszöget pedig további

1000

átló megrajzolásával tetszőleges módon háromszögekre bontjuk.

3. Határozzuk meg a legkisebb olyan

M

valós számot, amire az

\begin{matrix} | a b (a^{2} - b^{2}) + b c (b^{2} - c^{2}) + c a (c^{2} - a^{2}) | \leq M {(a^{2} + b^{2} + c^{2})}^{2} \end{matrix}

egyenlőtlenség teljesül minden

a

b

c

valós számra.

Erdélyi Márton megoldása.¹ Vegyük észre, hogy az egyenlőtlenség bal oldalán az abszolút érték belsejében álló kifejezés bármely két változó cseréje nyomán előjelet vált, és így bármely két változó különbségével osztható. Szorzattá alakítva kapjuk, hogy a bal oldal

| (a - b) (b - c) (c - a) (a + b + c) |

. Az

x = a - b

y = b - c

z = c - a

t = a + b + c

új változókat bevezetve egyrészt

x^{2} + y^{2} + z^{2} + t^{2} = 3 (a^{2} + b^{2} + c^{2})

, másrészt minden olyan

x

y

z

t

számnégyesre, amelyre

x + y + z = 0

, egyértelműen léteznek a megfelelő

a

b

c

mennyiségek. Keressük tehát a legkisebb olyan

M

számot, amelyre

\begin{matrix} | x y z t | \leq M \frac{{(x^{2} + y^{2} + z^{2} + t^{2})}^{2}}{9} . \end{matrix}

(1)

A három új változó,

x

y

és

z

között van két azonos előjelű, föltehető, hogy ezek

x

és

y

. Mindkettejüket a számtani közepükkel helyettesítve a bal oldal értéke nő (nem csökken), a jobb oldal értéke pedig csökken (nem nő). (Ez nyomban adódik a mértani, számtani és a négyzetes közepek közti egyenlőtlenségből.) Föltehető tehát, hogy

x = y (= - \frac{z}{2})

. Legyen

u = | x | = | y | = | \frac{z}{2} |

és

v = | t |

. Ezekkel a változókkal (1) a

\begin{matrix} 2 u^{3} v \leq M \frac{{(6 u^{2} + v^{2})}^{2}}{9} \end{matrix}

(2)

alakba írható. A (2) egyenlőtlenséget

\sqrt[]{2}

-vel szorozva kapjuk, hogy

\begin{matrix} \sqrt[]{8} u^{3} v \leq \frac{\sqrt[]{2}}{9} M {(6 u^{2} + v^{2})}^{2}, \end{matrix}

amit az alábbi alakban is írhatunk:

\begin{matrix} \sqrt[]{2} u \cdot \sqrt[]{2} u \cdot \sqrt[]{2} u \cdot v \leq \frac{\sqrt[]{2}}{9} M \cdot 16 {(\frac{{(\sqrt[]{2} u)}^{2} + {(\sqrt[]{2} u)}^{2} + {(\sqrt[]{2} u)}^{2} + v^{2}}{4})}^{2} . \end{matrix}

Negyedik gyököt vonva:

\begin{matrix} \sqrt[4]{\sqrt[]{2} u \cdot \sqrt[]{2} u \cdot \sqrt[]{2} u \cdot v} \leq \sqrt[4]{\frac{16 \sqrt[]{2}}{9} M} \sqrt[]{\frac{{(\sqrt[]{2} u)}^{2} + {(\sqrt[]{2} u)}^{2} + {(\sqrt[]{2} u)}^{2} + v^{2}}{4}} . \end{matrix}

(3)

M = \frac{9}{16 \sqrt[]{2}}

, akkor (3) éppen a mértani és a négyzetes közepek közti azonosan teljesülő egyenlőtlenség, ami azt jelenti, hogy

M \leq \frac{9}{16 \sqrt[]{2}}

. Ez a becslés viszont éles, ugyanis ha például

a = 3 + \sqrt[]{2}

b = \sqrt[]{2}

c = \sqrt[]{2} - 3

, akkor a feladat egyenlőtlenségében az egyenlőség teljesül. Az

M

keresett értéke így

\frac{9}{16 \sqrt[]{2}}

4. Határozzuk meg az összes olyan, egész számból álló

(x, y)

számpárt, amire teljesül

\begin{matrix} 1 + 2^{x} + 2^{2 x + 1} = y^{2} . \end{matrix}

(1)

Tomon István megoldása. Ha

x < 0

, akkor (1) bal oldala nagyobb

1

-nél és kisebb

4

-nél, tehát ekkor

y

nem egész.
Ha

x = 0

, akkor

y \in {- 2,2}

; két megoldást kapunk.
Ha

x = 1

, akkor

y^{2} = 11

, nem megoldás.
Ha

x = 2

, akkor

y^{2} = 37

, nem megoldás.
Ha

x > 2

, akkor

(1)

bal oldala páratlan, tehát ha

y

egész, akkor

y = 2 k + 1

valamilyen

k

egész számra. Ekkor (1)

1 + 2^{x} + 2^{2 x + 1} = {(2 k + 1)}^{2}

alakú, ahonnan rendezés után

\begin{matrix} 2^{x - 2} (1 + 2^{x + 1}) & = k (k + 1) . & (2) \end{matrix}

A jobb oldali szorzat egyik tényezője páratlan, a másik páros, így az, amelyik páros, osztható

2^{x - 2}

-nel. Az is föltehető, hogy

k

nem negatív, hiszen a

k

negatív, illetve nemnegatív értékeire

k (k + 1)

ugyanazokat az értékeket veszi fel. (2) bal oldala pozitív, így

k

is pozitív.
1. eset:

k

páros. Ekkor

2^{x - 2} | k

, azaz van olyan

b

pozitív egész, hogy

k = b \cdot 2^{x - 2}

. Ezt

(2)

-be írva

\begin{matrix} 2^{x - 2} (1 + 2^{x + 1}) & = b \cdot 2^{x - 2} (b \cdot 2^{x - 2} + 1), azaz \\ 1 + 2^{x + 1} & = b^{2} \cdot 2^{x - 2} + b . & (3) \end{matrix}

Innen leolvasható, hogy

b | 1 + 2^{x + 1}

, tehát

b

páratlan. Ha

b = 1

, akkor

1 + 2^{x + 1} > 2^{x - 2} + 1

(3)

jobb oldala kisebb, mint a bal. Ha

b > 1

, akkor

b \geq 3

, és így

\begin{matrix} b^{2} \cdot 2^{x - 2} + b \geq 9 \cdot 2^{x - 2} + 3 > 8 \cdot 2^{x - 2} + 1 = 2^{x + 1} + 1, \end{matrix}

(3) jobb oldala nagyobb, mint a bal. Az 1. esetben tehát nem kapunk újabb megoldást.
2. eset:

k + 1

páros. Ekkor

2^{x - 2} | k + 1

, azaz van olyan

c

pozitív egész, hogy

k = c \cdot 2^{x - 2} - 1

. Ezt

(2)

-be írva

\begin{matrix} 2^{x - 2} (1 + 2^{x + 1}) & = (c \cdot 2^{x - 2} - 1) c \cdot 2^{x - 2}, azaz \\ 1 + 2^{x + 1} & = c^{2} \cdot 2^{x - 2} - c . & (4) \end{matrix}

Most is igaz, hogy

c \geq 1

és páratlan, így az előzőhöz hasonló vizsgálatot végezhetünk.
Ha

c = 1

, akkor a

(4)

jobb oldala

2^{x - 2} - 1

, kisebb, mint a bal oldal, ekkor nem kapunk megoldást.
Ha

c = 3

, akkor a (4) egyenlőség

: 1 + 2^{x + 1} = 9 \cdot 2^{x - 2} - 3

. Rendezés után kapjuk, hogy

4 = 2^{x - 2}

, azaz

x = 4

. Ekkor (1) bal oldala

1 + 2^{4} + 2^{9} = 23^{2}

, két megoldást kapunk:

y = - 23

y = 23

.
Ha

c \geq 5

, akkor (4) jobb oldalát átalakítva

\begin{matrix} c^{2} \cdot 2^{x - 2} - c = 2^{x + 1} + (c^{2} - 8) 2^{x - 2} - c > 2^{x + 1} + c^{2} - 8 - c . \end{matrix}

c \geq 5

, akkor

c^{2} - 8 - c > 1

, tehát (4) jobb oldala nagyobb, mint a bal oldala, így több megoldást már nem kapunk.
A feladat feltételei tehát négy számpárra teljesülnek. Ezek:

(0; 2)

(0; - 2)

(4; 23)

(4; - 23)

5. Legyen

P (x)

egy egész együtthatós,

n > 1

fokú polinom, és legyen

k

egy pozitív egész. Tekintsük a

Q (x) = P (P (... P (P (x)) ...))

polinomot, ahol

P

k

-szor fordul elő. Bizonyítsuk be, hogy legfeljebb

n

darab olyan

t

egész szám van, amire

Q (t) = t

Kis Gergely megoldása. Tegyük fel, hogy létezik olyan

α_{0}

egész, amelyre

Q (α_{0}) = P^{(k)} (α_{0}) = α_{0}

és

P (α_{0}) \neq α_{0}

. Legyen

α_{j + 1} = P (α_{j})

és jelölje

i

azt a legkisebb pozitív egészt, amelyre

α_{i} = α_{0}

. Nyilván

2 \leq i \leq k

. Ismeretes, hogy ha

P (x)

egész együtthatós polinom,

a \neq b

egészek, akkor

a - b | P (a) - P (b)

, így fennállnak az alábbi oszthatóságok:

\begin{matrix} α_{1} - α_{0} | P (α_{1}) - P (α_{0}) = α_{2} - α_{1} | α_{3} - α_{2} | ... | α_{i} - α_{i - 1} | α_{i + 1} - α_{i} = α_{1} - α_{0} . \end{matrix}

x \neq y

egészek és

y \neq 0

, akkor

| y | \geq | x |

. Így, mivel a fenti oszthatósági láncban szereplő első és utolsó különbség azonos, ezeknek a különbségeknek az abszolút értéke állandó. Jelölje ennek az állandónak az értékét

φ

(

φ \neq 0

).
Azt állítjuk, hogy

α_{j + 1} - α_{j} = α_{j} - α_{j - 1}

nem teljesülhet minden

j

-re. Ellenkező esetben ugyanis

α_{0} \pm i φ = α_{i} = α_{0}

volna, vagyis

i φ = 0

, ami ellentmondás. Az

α_{j}

-k rendezése tehát nem monoton, van tehát olyan

j

, ahol megfordul, azaz

(α_{j + 1} - α_{j}) = (- 1) (α_{j} - α_{j - 1})

. Erre a

j

-re így

α_{j + 1} = α_{j - 1}

következik. Ekkor

P^{(i - j + 1)} (α_{j + 1}) = P^{(i - j + 1)} (α_{j - 1})

. Ez utóbbi egyenlőség pedig akkor és csak akkor teljesül, ha

α_{2} = α_{0}

, tehát

i = 2

, azaz

P (α_{0}) = α_{1}

és

P (α_{1}) = α_{0}

.
Legyenek ezután

β_{0}

és

β_{1}

olyan, az

α_{0}

α_{1}

számok mindegyikétől különböző egészek, amelyekre ugyancsak teljesül, hogy

P (β_{0}) = β_{1}

és

P (β_{1}) = β_{0}

. (

β_{0} = β_{1}

lehetséges.) Ekkor

α_{0} - β_{0} | α_{1} - β_{1} | α_{0} - β_{0}

és

α_{0} - β_{1} | α_{1} - β_{0} | α_{0} - β_{1}

. Ebből következik, hogy

\begin{matrix} α_{0} - β_{0} = α_{1} - β_{1} vagy α_{0} - β_{0} = β_{1} - α_{1} \end{matrix}

és

\begin{matrix} α_{0} - β_{1} = α_{1} - β_{0} vagy α_{0} - β_{1} = β_{0} - α_{1} . \end{matrix}

Rendezés után a két részállítás második tagja ugyanazt mondja:

\begin{matrix} α_{0} + α_{1} = β_{0} + β_{1}, \end{matrix}

(1)

az első tagok pedig:

α_{0} - α_{1} = β_{0} - β_{1}

, illetve

α_{0} - α_{1} = β_{1} - β_{0}

egyszerre nem teljesülhetnek, hiszen feltevésünk szerint

α_{0} - α_{1} \neq 0

. A két részállítás közül tehát legalább az egyikben a második tag teljesül, azaz (1) mindenképpen igaz, mégpedig attól függetlenül, hogy

β_{0}

és

β_{1}

egyenlők-e vagy sem.

I. Létezik olyan

α_{0}

egész, amelyre

P (P (α_{0})) = α_{0}

, de

P (α_{0}) \neq α_{0}

. Ekkor minden

t

egész számra, amelyre

Q (t) = t

, fennáll, hogy

P (t) + t = P (α_{0}) + α_{0}

. A

P (x) + x - P (α_{0}) - α_{0}

polinom

n

-edfokú, ezért legfeljebb

n

ilyen

t

létezik.

II. Nincs ilyen

α_{0}

egész. Ekkor minden olyan

t

egészre, amelyre

Q (t) = t

fennáll, arra

P (t) = t

is teljesül. Mivel a

P (x) - x

polinom

n

-edfokú, legfeljebb

n

darab ilyen

t

létezhet. Ezzel a feladat állítását igazoltuk.

6. Egy

P

konvex poligon mindegyik

b

oldalához hozzárendeljük a legnagyobb területű olyan háromszög területét, aminek egyik oldala

b

és ami benne van

P

-ben. Bizonyítsuk be, hogy a

P

oldalaihoz rendelt területek összege legalább a kétszerese

P

területének.

Paulin Roland megoldása. A sokszög mindegyik

b

oldalához létezik a szóban forgó maximális területű háromszög: ennek

b

-vel szemközti csúcsa a

b

egyenesétől legtávolabbi csúcs

P

-ben (3. ábra). A megoldás során egy

X Y Z

háromszög területét

[X Y Z]

-vel, a

P

sokszög területét pedig

[P]

-vel jelöljük.

3. ábra

Első észrevételünk az, hogy ha egy sokszög szögei között a

180^{\circ}

-ot is megengedjük és az oldalakon újabb csúcsokat veszünk fel, akkor sem

P

területe, sem a

P

oldalaihoz rendelt területek összege nem változik (4. ábra). Ezért

P

minden csúcsából húzzuk meg azt a félegyenest, amely

P

területét felezi (folytonossági meggondolások miatt ilyen félegyenes minden csúcshoz létezik), és e félegyenesnek a

P

határával való másik metszéspontját vegyük fel a csúcsok közé. Így az

A_{1} A_{2} A_{3} ... A_{2 n}

sokszöget kapjuk, melynek területét az

A_{i} A_{n + i}

egyenes minden

i

-re felezi (5. ábra). (Az indexelés

mod 2 n

ciklikus.)

4. ábra

5. ábra

A_{i} A_{n + i}

és

A_{i + 1} A_{n + i + 1}

egyenesek tehát felezik a sokszög területét, így a

P

belsejében metszik egymást (6. ábra); jelölje a metszéspontjukat

B_{i}

(

1 \leq i \leq n

). Ekkor

[A_{i} A_{i + 1} B_{i}] = [A_{n + i} A_{n + i + 1} B_{i}]

, hiszen

A_{i} A_{i + 1}

és

A_{n + i} A_{n + i + 1}

is felezi

P

területét. Legyen

t_{i} = [A_{i} A_{i + 1} B_{i}]

; ekkor

t_{i} = t_{n + i}

és

B_{i} = B_{n + i}

6. ábra

Azt állítjuk, hogy az

A_{i} A_{i + 1} B_{i}

háromszögek lefedik

P

-t, és így

\sum_{i = 1}^{2 n} t_{i} \geq [P]

. Ehhez vegyük észre, hogy adott

i

-re az

A_{i} A_{i + 1} B_{i}

és az

A_{n + i} A_{n + i + 1}

háromszögek belsejének egyesítése azon

P

-beli pontok halmaza, amelyek az

A_{i} A_{n + i}

és

A_{i + 1} A_{n + i + 1}

félegyenesek ellentétes partján vannak. (Ha egy

P

-beli

X

pont nincs ezeken a félegyeneseken, akkor ez azt jelenti, hogy az

A_{i} A_{n + i} X

és az

A_{i + 1} A_{n + i + 1} X

háromszögek ellenkező körüljárásúak.) Tekintsük ezután a

P

egy tetszőleges belső

X

pontját, amelyik egyik

A_{i} A_{i + 1}

félegyenesre sem illeszkedik. Ez a pont a fentiek értelmében az

A_{1} A_{n + 1}

és az

A_{n + 1} A_{1}

fégyenesek ellentétes partján van, így az

A_{1} A_{n + 1}, A_{2} A_{n + 2}, ..., A_{n} A_{2 n}, A_{n + 1} A_{1}

félegyenesek sorozatában van két szomszédos, az

A_{i} A_{n + i}

és az

A_{i + 1} A_{n + i + 1}

, amelyeknek

X

szintén az ellentétes partján van. Ez pedig éppen azt jelenti, hogy

X

benne van az

A_{i} A_{i + 1} B_{i}

és az

A_{n + i} A_{n + i + 1} B_{i}

háromszögek egyikében (6. ábra).
Legyen az

A_{i} A_{i + 1}

oldalhoz tartozó maximális területű háromszög területe

M_{i}

. Mivel

[A_{i} A_{i + 1} B_{i}] = [A_{n + i} A_{n + i + 1} B_{i}]

, ezért

B_{i} A_{i} \cdot B_{i} A_{i + 1} = B_{i} A_{n + i} \cdot B_{i} A_{n + i + 1}

. Ekkor vagy

B_{i} A_{i} \leq B_{i} A_{n + i}

és

B_{i} A_{i + 1} \geq B_{i} A_{n + i + 1}

vagy pedig

B_{i} A_{i} \geq B_{i} A_{n + i}

és

B_{i} A_{i + 1} \leq B_{i} A_{n + i + 1}

.
Az első esetben

\begin{matrix} \frac{[A_{i} A_{i + 1} A_{n + i}]}{[A_{i} A_{i + 1} B_{i}]} = \frac{A_{i} A_{n + i}}{A_{i} B_{i}} \geq 2, és így M_{i} \geq [A_{i} A_{i + 1} A_{n + i}] \geq 2 t_{i} . \end{matrix}

A második esetben hasonlóan kapjuk, hogy

\begin{matrix} \frac{[A_{i} A_{i + 1} A_{n + i + 1}]}{[A_{i} A_{i + 1} B_{i}]} = \frac{A_{i + 1} A_{n + i + 1}}{A_{i + 1} B_{i}} \geq 2, és így ekkor is M_{i} \geq [A_{i} A_{i + 1} A_{n + i + 1}] \geq 2 t_{i} . \end{matrix}

Mindenképpen igaz tehát, hogy

M_{i} \geq 2 t_{i}

. Ezeket az egyenlőtlenségeket összegezve kapjuk, hogy

\sum_{i = 1}^{2 n} M_{i} \geq 2 \sum_{i = 1}^{2 n} t_{i} \geq 2 [P]

, és ezt kellett bizonyítanunk.

¹Más megoldások alapján.