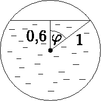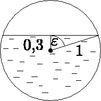Kezdőlap


Cím:	Megoldásvázlatok a 2006/3. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Czinki József
Füzet:	2006/április, 209 - 213. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész

a)

Van-e megoldása a következő egyenletnek a pozitív egész számok halmazán?

\begin{matrix} 1! + 2! + 3! + ... + x! = 2 y . \end{matrix}

b)

Oldjuk meg a következő egyenletet:

\begin{matrix} tg α + \sqrt[]{3} = \frac{\sqrt[]{2}}{cos α} . \end{matrix}

Megoldás.

a)

A feladat feltételéből következően

x

és

y

csak pozitív egész lehet.

1! = 1

n \geq 2

esetén

n!

páros, mert tartalmazza a 2-t szorzótényezőként. A bal oldali összeg tehát páratlan, a jobb oldal értéke viszont páros, az egyenletnek nincs megoldása.

b)

A nevezőben nem lehet 0, vagyis

cos α \neq 0

. Mindkét oldalt

cos α

-val szorozva és 2-vel osztva az

\frac{1}{2} sin α + \frac{\sqrt[]{3}}{2} cos α = \frac{\sqrt[]{2}}{2}

alakhoz jutunk. Felhasználva, hogy

cos \frac{π}{3} = \frac{1}{2}

és

sin \frac{π}{3} = \frac{\sqrt[]{3}}{2}

, a

sin α cos \frac{π}{3} + cos α sin \frac{π}{3} = \frac{\sqrt[]{2}}{2}

alak adódik, amit az addíciós tétel felhasználásával a

sin (α + \frac{π}{3}) = \frac{\sqrt[]{2}}{2}

alakra hozhatunk.
A megoldások:

α_{1} = - \frac{π}{12} + 2 k_{1} π

k_{1} \in Z

α_{2} = \frac{5 π}{12} + 2 k_{2} π

k_{2} \in Z

2. Sanyi félévi bizonyítványát mutatja a táblázat.

\begin{matrix} magyar irodalom & 5 (jeles) \\ magyar nyelv & 4 (jó) \\ történelem & 4 (jó) \\ matematika & 3 (közepes) \\ angol nyelv & 4 (jó) \\ német nyelv & 3 (közepes) \\ fizika & 2 (elégséges) \\ kémia & 3 (közepes) \\ biológia & 2 (elégséges) \\ rajz & 4 (jó) \\ ének-zene & 5 (jeles) \\ testnevelés & 5 (jeles) \end{matrix}

a)

Adjuk meg Sanyi jegyeinek móduszát, mediánját és terjedelmét.

b)

Számítsuk ki Sanyi tanulmányi átlagát (a jegyek számtani közepét).

c)

Adjuk meg az érdemjegyek szórását.

d)

Ábrázoljuk a jegyek százalékos eloszlását kördiagramon.

Megoldás.

a)

módusz: 4, medián: 4, terjedelem: 3.

b)

átlag: 3,667.

c)

szórás: 1,027.

d)

a jegyek

\begin{matrix} 25%-a & 5-ös, \\ 33,33%-a & 4-es, \\ 25%-a & 3-as, \\ 16,67%-a & 2-es. \end{matrix}

A jegyek eloszlása

3. Melyek azok az

x

pozitív egész számok, amelyekre igaz, hogy

x^{4} + 4

prímszám?

Megoldás.

x^{4} + 4

egész együtthatós polinomok szorzatává alakítható:

\begin{matrix} x^{4} + 4 & = x^{4} + 4 x^{2} + 4 - 4 x^{2} = {(x^{2} + 2)}^{2} - 4 x^{2} = {(x^{2} + 2)}^{2} - {(2 x)}^{2} = \\ = (x^{2} - 2 x + 2) (x^{2} + 2 x + 2) . \end{matrix}

Mivel

x

pozitív egész, a tényezők egészek és

0 < x^{2} - 2 x + 2 < x^{2} + 2 x + 2

. A szorzat csak úgy lehet prím, ha a kisebbik tényező értéke 1, a nagyobbik pedig prím. Ha

x^{2} - 2 x + 2 = 1

, akkor

x = 1

. Ebben az esetben a kifejezés értéke 5, valóban prím.
Csak

x = 1

esetén lesz

x^{4} + 4 (= 5)

prímszám.

4. Egy mértani sorozat első és harmadik elemének az összege

40

. Ha az első elemhez

4

-et, a második elemhez pedig

6

-ot adunk, akkor a harmadik elemmel együtt ugyanilyen sorrendben egy számtani sorozat három szomszédos eleméhez jutunk. Melyik ez a mértani sorozat?

Megoldás. A szokott módon jelöljük a mértani sorozat elemeit:

a_{1}

a_{1} q

a_{1} q^{2}

, a számtani sorozat három szomszédos eleme ekkor az

a_{1} + 4

a_{1} q + 6

a_{1} q^{2}

alakot ölti.
Az

a_{1} + a_{1} q^{2} = 40

egyenlet mellett felírható az

(a_{1} q + 6) - (a_{1} + 4) = a_{1} q^{2} - (a_{1} q + 6)

egyenlet is. Az így kapott egyenletrendszer mindkét egyenletéből kifejezzük az

a_{1}

-et (

q \neq 1

), ekkor kapjuk:

\frac{5}{1 + q^{2}} = \frac{1}{{(q - 1)}^{2}}

.
Ebből két megoldást kapunk:

q = 2

a_{1} = 8

, valamint

q = 0, 5

a_{1} = 32

. Mindkettő megoldása a feladatnak.

II. rész

5. Milyen arányban osztja az

y

tengely az

f (x) = x^{2} - 4

és a

g (x) = - x^{2} - 2 x

függvények görbéi által határolt területet?

Megoldás. A két függvény metszéspontjainak abszcisszái:

x_{1} = - 2

x_{2} = 1

(- 2; 1)

intervallumban a két függvény különbsége állandó előjelű, így a szóban forgó területek aránya

\begin{matrix} λ = \frac{\int_{- 2}^{0} f (x) - g (x) d x}{\int_{0}^{1} f (x) - g (x) d x}, \\ \int f (x) - g (x) d x = \int 2 x^{2} + 2 x - 4 d x = \frac{2}{3} x^{3} + x^{2} - 4 x + c . \end{matrix}

Belyettesítve:

\begin{matrix} {[\frac{2}{3} x^{3} + x^{2} - 4 x]}_{- 2}^{0} = - \frac{20}{3} és {[\frac{2}{3} x^{3} + x^{2} - 4 x]}_{0}^{1} = - \frac{7}{3} . \end{matrix}

(Innen az is látszik, hogy a

(- 2; 1)

intervallumon

f (x) < g (x)

.) A területek aránya tehát

\begin{matrix} λ = (- \frac{20}{3}) : (- \frac{7}{3}) = \frac{20}{7} . \end{matrix}

6. Egy henger alakú fekvő tartály alapkörének a sugara 1 m, a henger alkotója 3 m. A tartályban a víz magassága jelenleg 1,6 m. A víz egy részét kiengedjük egy elegendően nagy térfogatú, álló henger alakú edénybe. Az edény alapkörének sugara 0,5 m. Milyen magas lesz ebben az edényben a vízszint, ha a fekvő hengerben 0,3 m-t süllyedt a víz magassága?

Megoldás. Számoljuk ki a fekvő henger kezdeti víztartalmát:

\begin{matrix} cos φ = \frac{0, 6}{1}, φ \approx 53, 13^{\circ} . \\ T_{körszelet} = \frac{2 φ}{360^{\circ}} \cdot r^{2} π - \frac{1}{2} r^{2} \cdot sin 2 φ \approx 0, 9273 - 0, 4800 = 0, 4473 m^{2}.T_{1}=r^{2}π-T_{körszelet}\approx3,1416-0,4473= 2,6943 m^{2}.V_{1}=T_{1}d\approx8,083 m^{3}. \end{matrix}

A fekvő hengerben maradt víz térfogatának kiszámítása:

\begin{matrix} cos ε = \frac{0, 3}{1}, ε \approx 72, 54^{\circ} . \\ T_{{körszelet}_{2}} = \frac{2 ε}{360} \cdot r^{2} π - \frac{1}{2} r^{2} \cdot sin 2 ε \approx 1, 2661 - 0, 2862 = 0, 9799 m^{2}.T_{2}=r^{2}π-T_{{körszelet}_{2}}\approx3,1416- 0,9799\approx2,1617 m^{2}.V_{2}=T_{2}d\approx6,4851 m^{3}. \end{matrix}

A fekvő hengerből kifolyt víz térfogata:

V \approx 1, 5978 m^{3}

Az álló hengerben a vízmagasság kiszámítása:

\begin{matrix} V_{henger} = r^{2} π \cdot m, vagyis 1, 598 \approx 0, 25 \cdot 3, 14 \cdot m, \end{matrix}

amiből

m \approx 2, 03 m

.
Tehát körülbelül 2 méter magasan áll majd a víz a második hengerben.

7. Egy üzem azt a megrendelést kapta, hogy készítsen el 100 db 1 dm

^{3}

térfogatú felül nyitott kúp alakú fagylalttölcsért. Az alapanyag drága, a megrendelő pedig csak a kúp térfogatát írta elő. Milyen nyílásszögű kúp esetén lesz minimális az anyagköltség?

Megoldás. A kúp térfogata:

\frac{r^{2} π \cdot m}{3} = 1000 cm^{3}

. A kúp alkotója a sugárral és a magassággal kifejezve:

a = \sqrt[]{r^{2} + m^{2}}

. A kúppalást felszíne:

A_{palást} = r \cdot π \cdot a

.
Kell, hogy

\begin{matrix} A = r π \sqrt[]{r^{2} + {(\frac{3000}{r^{2} π})}^{2}} = π \sqrt[]{r^{4} + \frac{9 000 000}{r^{2} π^{2}}} \end{matrix}

minimális legyen. Elég megkeresni az

r^{4} + \frac{9 000 000}{r^{2} π^{2}}

kifejezés minimumát. A deriváltat egyenlővé téve 0-val:

\begin{matrix} [r^{4} + \frac{9 000 000}{r^{2} π^{2}}]' = 4 r^{3} + \frac{- 2 r π^{2} \cdot 9 000 000}{r^{4} π^{4}} = 0, \end{matrix}

ahonnan

4 r^{3} = \frac{2 π^{2} \cdot 9 000 000}{r^{3} π^{4}}

, vagyis

r^{6} = \frac{18 000 000}{4 π^{2}} \approx 455 945, 33

r \approx 8, 773

cm adódik.
A második deriváltat vizsgálva az

r = 8, 773

helyen:

\begin{matrix} [4 r^{3} - \frac{2 r π^{2} \cdot 9 000 000}{r^{4} π^{4}}]' = [4 r^{3} - \frac{18 000 000}{r^{3} π^{2}}]' = 12 r^{2} - \frac{- 18 000 000 \cdot 3 r^{2} π^{2}}{r^{6} π^{4}} > 0. \end{matrix}

A palást felszíne minimális, ha

r \approx 8, 773

cm. Ekkor

m \approx 12, 407

cm,

tg \frac{φ}{2} = \frac{r}{m}

, ahonnan a keresett nyílásszög

φ \approx 70, 53^{\circ}

8. Hol lehet annak a derékszögű háromszögnek a derékszögű csúcsa, melynek területe

25

egység, és az átfogójának a két végpontja

A (1; - 2)

és

B (6; 8)

Megoldás. Az ilyen derékszögű háromszög harmadik csúcsa az

A B

szakasz Thalész-körének és az

A B

egyenesétől

2 \sqrt[]{5}

egységre haladó,

A B

-vel párhuzamos

e_{1}

és

e_{2}

egyeneseknek a metszéspontja lesz.
Ugyanis az

A B

szakasz hossza:

d_{A B} = \sqrt[]{{(6 - 1)}^{2} + {(8 - (- 2))}^{2}} = \sqrt[]{125}

. A háromszög területe:

T = d_{A B} \cdot m \cdot \frac{1}{2}

. Ezekből adódik, hogy

2 \sqrt[]{5} = m

.
A Thalész-kör egyenlete:

{(x - 3, 5)}^{2} + {(y - 3)}^{2} = \frac{125}{4}

.
Az

e_{1}

és

e_{2}

egyenesek egy irányvektora:

\vec{A B} (5; 10)

. Egy normálvektoruk:

n_{e_{1}} = n_{e_{2}} (- 10; 5)

. Állítsunk az

A B

-re

O

-ban egy

f

merőleges egyenest. Az

f

egyenes egyenlete:

x + 2 y = 9, 5

. Ezt elmetszve az

O

középpontú

m

sugarú körrel, melynek egyenlete

{(x - 3, 5)}^{2} + {(y - 3)}^{2} = 20

e_{1}

, illetve

e_{2}

egy-egy pontját kapjuk:

M_{1} (- 0, 5; 5)

M_{2} (7, 5; 1)

e_{1}

egyenlete:

- 2 x + y = 6

e_{2}

egyenlete:

- 2 x + y = - 14

. A feladatnak négy megoldása van:

e_{1}

és a Thalész-kör metszéspontjai:

C_{1} (1; 8)

C_{2} (- 2; 2)

;

e_{2}

és a Thalész-kör metszéspontjai:

C_{3} (9; 4)

C_{4} (6; - 2)

a)

Van-e egy

25

fős társaságban

3

olyan ember, akik ugyanabban a hónapban születettek? Indokoljuk a választ.

b)

Az egyjegyű pozitív egész számok halmazából kiválasztunk egy tetszőleges részhalmazt. Mi a valószínűsége, hogy ebben az

1

vagy a

2

benne van?

c)

Az egyjegyű pozitív egész számok halmazából maximum hány olyan részhalmazt tudunk kiválasztani, amelyek közül bármely kettőnek van közös eleme?

Megoldás.

a)

A skatulya-elv szerint lesz legalább 1 olyan hónap, amikor legalább három ember született, hiszen

2 \cdot 12 = 24 < 25

. Az e hónapban születettek közül bármely három megfelelő.

b)

A halmaz elemei: 1, 2, 3, 4, 5, 6, 7, 8, 9. Ez egy kilencelemű halmaz, tehát az összes részhalmazainak száma

2^{9}

. Azon részhalmazok száma, melyekben sem az 1, sem a 2 nem szerepel

2^{7}

. A keresett valószínűség:

P = 1 - \frac{2^{7}}{2^{9}} = \frac{3}{4}

c)

Válasz:

2^{8}

. Az olyan részhalmazok száma, amelyekben pl. az 1 benne van,

2^{8}

, tehát

2^{8}

db a feltételeknek megfelelő részhalmazt biztosan ki tudunk választani. Minden egyes részhalmaz kiválasztásakor egyúttal a komplementerét is ,,kiválasztjuk'', vagyis mondhatjuk, hogy a részhalmazok halmaza részhalmaz és komplementer részhalmaz típusú párokba rendezhető. Mivel a párok száma az összes részhalmazok számának a fele,

2^{8}

, azért ennél több részhalmaz között már van ilyen ‐ részhalmaz és komplementer részhalmaz ‐ páros. Ezeknek nincs közös elemük, tehát

2^{8} + 1

db a feltételeknek megfelelő részhalmaz nem választható ki.