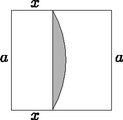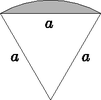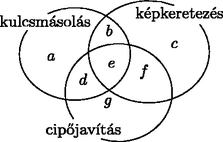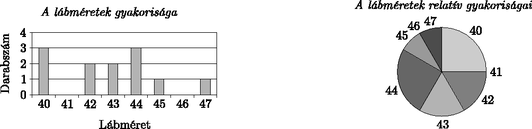Cím:	Megoldásvázlatok a 2005/6. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Czinki József
Füzet:	2005/októberi melléklet, 26 - 31. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. $50$ liter $80\%$-os töménységű etilalkoholt tartalmazó edényből valamennyit kivettünk, majd a hiányt vízzel pótoltuk. Ezután a keverékből $3$ literrel kevesebbet vettünk ki, mint előzőleg, és ezt a hiányt is vízzel pótoltuk. Jelenleg az edényben az etilalkohol és a víz mennyisége azonos. Hány liter folyadékot vettünk ki először?   Megoldás. Az alkohol eredeti mennyisége az edényben: $50\cdot 0\mathrm{,}8=40$ liter. Az $x$ liter kivétele után $40-x\cdot 0\mathrm{,}8$ liter alkohol marad az edényben. Az oldat $\frac{40-x\cdot 0\mathrm{,}8}{50}\cdot 100$ százalékos töménységű lesz, ha a hiányt vízzel pótoljuk. A következő alkalommal $\left(x-3\right)\cdot \frac{40-x\cdot 0\mathrm{,}8}{50}$ liter alkoholt veszünk ki. Felírható a következő egyenlet: $\begin{array}{c}{\displaystyle 40-x\cdot 0\mathrm{,}8-\left(x-3\right)\cdot \frac{40-x\cdot 0\mathrm{,}8}{50}=25.}\end{array}$ Rendezzük és megoldjuk a másodfokú egyenletet, a feladatnak csak az egyik gyök lesz megoldása: $x\approx 11\mathrm{,}94$ liter.   2. Fejezzük ki az $x$ értékét az $a$ segítségével, ha tudjuk, hogy az $a$ sugarú körív felezi az $a$ oldalú négyzet területét.     Megoldás. A satírozott körszelet területe $T$ (1. ábra), ekkor: 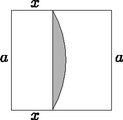$\begin{array}{c}{\displaystyle ax+T=\frac{a^2}{2}\mathrm{.}}\end{array}$     1. ábra   A 2. ábrán látható, hogy a körszelethez tartozó középponti szög ${60}^{\circ }$-os. Ebből adódóan: $\begin{array}{c}{\displaystyle T=\frac{a^2\pi }{6}-\frac{a^2\sqrt[]{3}}{4}\mathrm{.}}\end{array}$ Ezt behelyettesítve a következő egyenletet kapjuk: 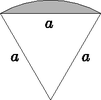$\begin{array}{c}{\displaystyle ax+\frac{a^2\pi }{6}-\frac{a^2\sqrt[]{3}}{4}=\frac{a^2}{2}\mathrm{.}}\end{array}$ Vagyis: $x=a\left(\frac{1}{2}+\frac{\sqrt[]{3}}{4}-\frac{\pi }{6}\right)\approx 0\mathrm{,}41a$.     2. ábra   3. Szabadon engedtünk $41$ méhet egy téglatest alakú helyiségben melynek élhosszúságai: 5 m, 4 m, 2 m. Bizonyítsuk be, hogy bármely időpillanatban létezik $2$ olyan méhecske, melyek távolsága 1,8 m-nél kisebb.   Megoldás. A helyiség térfogata $40\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$. Osszuk fel a helyiséget 40 db $1\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$ térfogatú kockára, és tekintsük a méhecskéket pontszerűnek. Minden méhecske tartozzon ahhoz a kockához, amelyikben tartózkodik. (A határfelületen tartózkodó méhecskéket is soroljuk hozzá valamely olyan kockához, melynek a határfelületén tartózkodnak.) A skatulya-elv értelmében lesz legalább egy olyan kocka, amelyhez két méhecske tartozik. E két méhecske távolsága kisebb, mint 1,8 m, hiszen az 1 m élhosszúságú kocka testátlója $\sqrt[]{3}\approx 1\mathrm{,}732$ m hosszú.   4. $a)$ Valaki autóvásárlásra $10000$ euró kölcsönt vett fel $10$ év futamidőre, évi $8\%$ kamatra, évenkénti törlesztéssel. Mennyit kell évente visszafizetnie? (A törlesztő részlet minden évben azonos.) $b)$ Legalább hány évre kell felvennie a kölcsönt, ha legfeljebb évi $2200$ eurót szeretne visszafizetni?   Megoldás. $a)$ Minden egyes $x$ évi részlet visszafizetésével az $x$ részlet hátralévő kamatainak megfizetésétől is mentesül. Ennek alapján felírható: $\begin{array}{c}{\displaystyle 10000\cdot 1\mathrm{,}{08}^{10}-x\cdot 1\mathrm{,}{08}^9-x\cdot 1\mathrm{,}{08}^8-x\cdot 1\mathrm{,}{08}^7-\text{...}-x\cdot 1\mathrm{,}{08}^2-x\cdot 1\mathrm{,}08-x=0.}\end{array}$ Ezt átírhatjuk a következő alakba a mértani sorozat összegképlete alapján: $\begin{array}{c}{\displaystyle 10000\cdot 1\mathrm{,}{08}^{10}-x\cdot \frac{1\mathrm{,}{08}^{10}-1}{1\mathrm{,}08-1}=0.}\end{array}$ Ezt megoldva: $x\approx 1490\mathrm{,}3$ euró. $b)$ Az előző feladatrészhez hasonló megfontolással felírható: $\begin{array}{c}{\displaystyle 10000\cdot 1\mathrm{,}{08}^n-2200\cdot \left(\frac{1\mathrm{,}{08}^n-1}{1\mathrm{,}08-1}\right)=0.}\end{array}$ Ennek megoldása: $n\approx 5\mathrm{,}87$. Tehát legalább 6 évre kellene felvennie a kölcsönt.   II. rész   5. $a)$ Oldjuk meg a $\text{sin}2x+1=3\left(\text{sin}x+\text{cos}x\right)-2$ egyenletet. $b)$ Milyen $n$ természetes számra lesz a $3\cdot 5^n+n^2+4n+4$ kifejezés osztható $100$-zal?   Megoldás. $a)$ Alkalmazva a megfelelő összefüggéseket, a feladat egy másodfokú egyenletre vezet: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 2\text{sin}x\text{cos}x+\text{sin}{}^{2}x+\text{cos}{}^{2}x=3\left(\text{sin}x+\text{cos}x\right)-\mathrm{2,}}\hfill \\ \hfill {\displaystyle {\left(\text{sin}x+\text{cos}x\right)}^2-3\left(\text{sin}x+\text{cos}x\right)+2=0.}\hfill \end{array}}$ Ennek megoldásai: ${\left(\text{sin}x+\text{cos}x\right)}_1=2$ és ${\left(\text{sin}x+\text{cos}x\right)}_2=1$. A $\text{sin}x+\text{cos}x=2$ nem vezet megoldásra. A $\text{sin}x+\text{cos}x=1$ esetén $x_1=2k\pi$, $k\in \text{Z}$ és $x_2=\frac{\pi }{2}+2l\pi$, $l\in \text{Z}$ adódik. $b)$ A $3\cdot 5^n+n^2+4n+4$ kifejezés $n=0$ és $n=1$ esetén nem osztható 100-zal. Az $5^n$ kifejezésről $n\ge 2$ esetén könnyen belátható, hogy 25-re végződik. Ebből adódóan a $3\cdot 5^n$ két utolsó számjegye 75. A 100-zal való oszthatóság feltétele, hogy $n^2+4n+4={\left(n+2\right)}^2$ 25-re végződjön. Könnyű belátni, hogy egy természetes szám négyzete akkor és csak akkor végződik 25-re, ha a természetes szám utolsó számjegye 5. Tehát $n=3+k\cdot 10$ ahol $k$ nemnegatív egész szám.   6. Adottak a következő függvények: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle }& {\displaystyle f:x\in \left[-5;10\right[\mathrm{,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle x\mapsto |||x-2|-2|-2|\mathrm{,}}\\ \hfill {\displaystyle }& {\displaystyle g:x\in \left]-1;4\right]\mathrm{,}}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle x\mapsto -x^2+4x+2.}\end{array}}$ $a)$ Ábrázoljuk közös koordináta rendszerben az $f$ és a $g$ függvényeket. $b)$ Milyen $x$ értékekre igaz, hogy $f\left(x\right)>g\left(x\right)$? $c)$ Számítsuk ki a két függvénygörbe által bezárt síkidom területét.   Megoldás. $a)$     $b)$ $x\in \left]-1;0\right[$. $c)$ A kérdéses síkidomot két részre vágjuk. Az egyik egy háromszög, ennek a területe könnyen meghatározható, a másik rész területét integrálással számítjuk ki. $\begin{array}{c}{\displaystyle T=\frac{4\cdot 2}{2}+\underset{-2}{\overset{2}{\int }}\left(-x^2+4\right)dx=4+{\left[-\frac{x^3}{3}+4x\right]}_{-2}^2=4+\frac{32}{3}=\frac{44}{3}\mathrm{.}}\end{array}$   7. Térképésztanulók $3$ dimenziós koordináta-rendszerbe foglalták egy felülnézetből 1000 m-szer 1000 m-es nagyságú, négyzet alakú terepszakasz adatait. Az origó a terület délnyugati sarokpontja, melynek tengerszintfeletti magassága 320 m. A tereppontok koordinátái méterben értendők. Az első koordináta $\left(x\right)$ a keleti, a második $\left(y\right)$ pedig az északi irányban vett kiterjedést jelöli. A függőleges kiterjedéseket a koordinátahármasok harmadik tagja $\left(z\right)$ jelöli. ($z$ lehet negatív is.) $a)$ Milyen emelkedési szögben látszik az $A\left(31;40;110\right)$ magaslatról a $B\left(221;52;340\right)$ magaslat? $b)$ Mi az $A$ és a $B$ magaslatokat összekötő egyenes $x$ és $y$ tengelyek által meghatározott síkra vonatkozó merőleges vetületének egyenlete az $x$, $y$ koordinátarendszerben? $c)$ Mekkora a tengerszint feletti magassága annak a sziklának, melynek $C$ csúcsa a $D\left(400;400;30\right)$, $E\left(500;500;30\right)$, $F\left(500;400;30\right)$ pontokkal együtt $100000\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$ térfogatú gúlát határoz meg?   Megoldás. $a)$ Az $AB$ szakasz egy olyan derékszögű háromszög átfogója, melynek egyik (függőleges) befogója $340-110=230$ m hosszú, másik befogójának hossza az $A$ és a $B$ pont $x$ és $y$ tengelyekkel kijelölt síkra vonatkozó merőleges vetületeinek távolsága: $\begin{array}{c}{\displaystyle \sqrt[]{{\left(221-31\right)}^2+{\left(52-40\right)}^2}\approx 190\mathrm{,}379\text{m. }}\end{array}$ Az emelkedési szögre: $\text{tg}\alpha =\frac{230}{190\mathrm{,}379}$, ebből $\alpha \approx 50\mathrm{,}{38}^{\circ }$ adódik. $b)$ Az $x$, $y$ rendszerben az $A\text{'}\left(31;40\right)$ és a $B\text{'}\left(221;52\right)$ pontokon áthaladó egyenes egyenletét kell felírni. Egyik irányvektora: $\text{v}\left(190;12\right)$, normálvektora: $\text{n}\left(-12;190\right)$. A kérdéses egyenes egyenlete: $-12x+190y=7228$. $c)$ A $z$ koordináták egyenlők, azért a $D$, $E$, $F$ pontok egy az $x$ és $y$ tengelyekkel kijelölt síkkal párhuzamos helyzetű háromszöget határoznak meg. A koordináták alapján a $DEF$ háromszög egy 100 m hosszú befogókkal rendelkező egyenlő szárú derékszögű háromszög, melynek területe: $\begin{array}{c}{\displaystyle T=\frac{100\cdot 100}{2}=5000\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>. }}\end{array}$ A gúla térfogata: $V=\frac{T\cdot m}{3}$, azért $\begin{array}{c}{\displaystyle 100000=\frac{5000\cdot m}{3}\mathrm{.}}\end{array}$ Innen $m=60$ m, a $C$ pont tengerszint feletti magassága kétféle lehet: $320+30+60=410$ m vagy $320+30-60=290$ m.   8. Egy nagyvárosban $21$ szolgáltatóház működik. Ezek közül tizenháromban vállalnak kulcsmásolást, tizenegyben képkeretezést, és nyolc szolgáltatóház vállal cipőjavítást. Az összes szolgáltatóház nyújtja valamelyiket az előző három szolgáltatás közül. Négy olyan szolgáltatóház van, ahol nem vállalnak képkeretezést, és cipőt sem javítanak. Három szolgáltatóház a kérdéses három szolgáltatás közül csak cipőjavítást nem vállal. Csak egy olyan szolgáltatóház van, amely cipőt javít, de a másik két szolgáltatást nem nyújtja. $a)$ Mutassuk meg, hogy nincs két olyan szolgáltatóház, amely mindhárom említett szolgáltatást nyújtja. $b)$ Hány olyan szolgáltatóház van, amely csak képet keretez a kérdéses három szolgáltatás közül? $c)$ Úgy értesültünk, hogy a következő héten valamelyik szolgáltatóház a kérdéses három szolgáltatás közül egy újat emel a profiljába. Mi a valószínűsége annak, hogy ezzel lesz két olyan szolgáltatóház, amely mindhárom említett szolgáltatást nyújtja?   Megoldás. Készítsük el a mellékelt diagramot, és gondolatban minden szolgáltatóházat helyezzünk el a megfelelő helyen. Az $a$, $b$, $c$, $d$, $e$, $f$, $g$ betűk a tartományok által szemléltetett halmazok elemszámát jelentik. $a)$ A szövegből látható, hogy $a=4$, $b=3$, $g=1$. Felírható: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a+b+c+d+e+f+g}& {\displaystyle =\mathrm{21,}}\hfill \\ \hfill {\displaystyle a+b+d+e}& {\displaystyle =\mathrm{13,}}\hfill \\ \hfill {\displaystyle b+c+e+f}& {\displaystyle =\mathrm{11,}}\hfill \\ \hfill {\displaystyle d+e+f+g}& {\displaystyle =8.}\hfill \end{array}}$ Az egyenletrendszert megoldva: $e=1$, ezzel igazoltuk az állítást.     $b)$ Az előző egyenletrendszerből: $c=6$. $c)$ Összesen 20 szolgáltatóház tud a feltételek mellett profilt bővíteni, ez az elemi események száma. A kedvező események száma: $b+d+f=3+5+1=9$ ($d$ és $f$ értéke szintén az $a)$ részben felírt egyenletrendszerből származik). A kérdéses valószínűség: $P=\frac{9}{20}$.   9. Egy sportiskola $12$ fős csoportjának néhány adatát tartalmazza a következő táblázat:   ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{Sorszám a}}\hfill & \hfill {\displaystyle \text{Testmagasság}}\hfill & \hfill {\displaystyle \text{Lábméret}}\hfill & \hfill {\displaystyle \text{Egyéni csúcs}}\hfill & \hfill {\displaystyle \text{Egyéni csúcs}}\hfill \\ \hfill {\displaystyle \text{ naplóban}}\hfill & \hfill {\displaystyle \text{(cm)}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{távolugrásban}}\hfill & \hfill {\displaystyle \text{távolugrásban}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{2004-ben (cm)}}\hfill & \hfill {\displaystyle \text{2005-ben (cm)}}\hfill \\ \hfill {\displaystyle \text{1.}}\hfill & \hfill {\displaystyle \text{169}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{401}}\hfill & \hfill {\displaystyle \text{429}}\hfill \\ \hfill {\displaystyle \text{2.}}\hfill & \hfill {\displaystyle \text{180}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{432}}\hfill & \hfill {\displaystyle \text{425}}\hfill \\ \hfill {\displaystyle \text{3.}}\hfill & \hfill {\displaystyle \text{159}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{370}}\hfill & \hfill {\displaystyle \text{405}}\hfill \\ \hfill {\displaystyle \text{4.}}\hfill & \hfill {\displaystyle \text{191}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{520}}\hfill & \hfill {\displaystyle \text{531}}\hfill \\ \hfill {\displaystyle \text{5.}}\hfill & \hfill {\displaystyle \text{181}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{462}}\hfill & \hfill {\displaystyle \text{461}}\hfill \\ \hfill {\displaystyle \text{6.}}\hfill & \hfill {\displaystyle \text{176}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{448}}\hfill & \hfill {\displaystyle \text{482}}\hfill \\ \hfill {\displaystyle \text{7.}}\hfill & \hfill {\displaystyle \text{174}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{430}}\hfill & \hfill {\displaystyle \text{422}}\hfill \\ \hfill {\displaystyle \text{8.}}\hfill & \hfill {\displaystyle \text{170}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{419}}\hfill & \hfill {\displaystyle \text{426}}\hfill \\ \hfill {\displaystyle \text{9.}}\hfill & \hfill {\displaystyle \text{173}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{359}}\hfill & \hfill {\displaystyle \text{380}}\hfill \\ \hfill {\displaystyle \text{10.}}\hfill & \hfill {\displaystyle \text{188}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{602}}\hfill & \hfill {\displaystyle \text{581}}\hfill \\ \hfill {\displaystyle \text{11.}}\hfill & \hfill {\displaystyle \text{201}}\hfill & \hfill {\displaystyle \text{47}}\hfill & \hfill {\displaystyle \text{‐}}\hfill & \hfill {\displaystyle \text{473}}\hfill \\ \hfill {\displaystyle \text{12.}}\hfill & \hfill {\displaystyle \text{169}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{388}}\hfill & \hfill {\displaystyle \text{388}}\hfill \\ \hline\end{array}}$   $a)$ Számítsuk ki, hány százalékkal változtak a diákok egyéni csúcsai távolugrásban $2004$-ről $2005$-re? Állítsuk sorba a diákok naplóbeli sorszámát e változás növekvő sorrendje alapján. $b)$ Ábrázoljuk a lábméretek gyakoriságát, illetve relatív gyakoriságát a megfelelő diagramokon. $c)$ Hányféleképpen választható ki három diák úgy, hogy van köztük az átlagnál alacsonyabb is és magasabb is?   Megoldás. $a)$ A növekedés mértékére kapott adatokat az 1. táblázat tartalmazza. A naplóbeli sorszámok sorrendjét a növekedés mértékének növekvő sorrendje alapján a második táblázat mutatja. A 11. sorszámú diák esetén hiányzó adat miatt nem tudunk számolni.   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{Sorszám}}\hfill & \hfill {\displaystyle \text{A növekedés}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{mértéke}}\hfill \\ \hfill {\displaystyle \text{1.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>6</mn><mn>,</mn><mn>98</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{2.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mn>,</mn><mn>62</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{3.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>9</mn><mn>,</mn><mn>46</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{4.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>2</mn><mn>,</mn><mn>12</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{5.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0</mn><mn>,</mn><mn>22</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{6.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>7</mn><mn>,</mn><mn>59</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{7.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mn>,</mn><mn>86</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{8.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>1</mn><mn>,</mn><mn>67</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{9.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>5</mn><mn>,</mn><mn>85</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{10.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>3</mn><mn>,</mn><mn>49</mn><mo>\%</mo></math>}}\hfill \\ \hfill {\displaystyle \text{11.}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{12.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>0</mn><mn>,</mn><mn>00</mn><mo>\%</mo></math>}}\hfill \\ \hline\end{array}}$   1. táblázat   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{A növekedés}}\hfill & \hfill {\displaystyle \text{Sorszám}}\hfill \\ \hfill {\displaystyle \text{mértéke}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>3</mn><mn>,</mn><mn>49</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{10.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mn>,</mn><mn>86</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{7.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mn>,</mn><mn>62</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{2.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>0</mn><mn>,</mn><mn>22</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{5.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>0</mn><mn>,</mn><mn>00</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{12.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>1</mn><mn>,</mn><mn>67</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{8.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>2</mn><mn>,</mn><mn>12</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{4.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>5</mn><mn>,</mn><mn>85</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{9.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>6</mn><mn>,</mn><mn>98</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{1.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>7</mn><mn>,</mn><mn>59</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{6.}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mo stretchy="false">-</mo></mphantom><mn>9</mn><mn>,</mn><mn>46</mn><mo>\%</mo></math>}}\hfill & \hfill {\displaystyle \text{3.}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$   2. táblázat   $b)$ A táblázat mutatja a gyakoriságok és a relatív gyakoriságok értékeit.   ${\displaystyle \begin{array}{|ccccccccc|}\hline \hfill {\displaystyle \text{Méret}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{47}}\hfill \\ \hfill {\displaystyle \text{Gyakoriság}}\hfill & \hfill {\displaystyle \text{3}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{3}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{1}}\hfill \\ \hfill {\displaystyle \text{Relatív gyakoriság}}\hfill & \hfill {\displaystyle \text{25\%}}\hfill & \hfill {\displaystyle \text{0\%}}\hfill & \hfill {\displaystyle \text{16,67\%}}\hfill & \hfill {\displaystyle \text{16,67\%}}\hfill & \hfill {\displaystyle \text{25\%}}\hfill & \hfill {\displaystyle \text{8,33\%}}\hfill & \hfill {\displaystyle \text{0\%}}\hfill & \hfill {\displaystyle \text{8,33\%}}\hfill \\ \hline\end{array}}$     $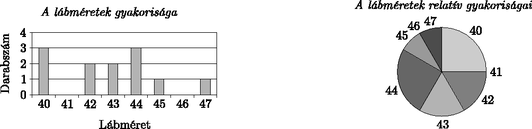c)$ Az átlagmagasság értéke: $\begin{array}{c}{\displaystyle K=\frac{169+180+159+191+181+176+174+170+173+188+201+169}{12}\approx 177\mathrm{,}58.}\end{array}$ 7 fő ennél alacsonyabb és 5 fő ennél magasabb. Összesen $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{12}{3}\right)=\frac{12!}{9!\cdot 3!}=220}\end{array}$ eredménye lehet a sorsolásnak. Ezek közül $\left(\genfrac{}{}{0ex}{}{7}{3}\right)=\frac{7!}{4!\cdot 3!}=35$ esetben csupa az átlagmagasságnál alacsonyabb, $\left(\genfrac{}{}{0ex}{}{5}{3}\right)=\frac{5!}{2!\cdot 3!}=10$ esetben csupa az átlagmagasságnál magasabb diák választódik ki. $220-35-10=175$ esetben lesz a három kisorsolt diák közt az átlagnál alacsonyabb és az átlagnál magasabb diák is.