Cím:	Megoldásvázlatok a 2005/9. sz.emelt szintű gyakorló feladataihoz
Szerző(k):	Czinki József
Füzet:	2006/január, 18 - 22. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. $a)$ A gráf minden élét pontosan egyszer tartalmazó vonalat Euler-vonalnak, az olyan Euler-vonalat, amelynek a kezdő és a végpontja egybeesik, Euler-körnek nevezzük. Az ábrán látható három gráf közül mely gráfoknak van Euler-vonala, illetve Euler-köre?     $b)$ Milyen számjegyeket helyettesíthetnek a betűk, ha $\text{R}=0$, különböző betűk különböző számokat jelölnek és az összeadás természetesen helyes eredményt ad? ${\displaystyle \begin{array}{ccccc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{O}}\hfill & \hfill {\displaystyle \text{R}}\hfill & \hfill {\displaystyle \text{O}}\hfill & \hfill {\displaystyle \text{L}}\hfill \\ \hfill {\displaystyle \text{ +}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{A}}\hfill & \hfill {\displaystyle \text{M}}\hfill & \hfill {\displaystyle \text{O}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{A}}\hfill & \hfill {\displaystyle \text{R}}\hfill & \hfill {\displaystyle \text{R}}\hfill & \hfill {\displaystyle \text{A }}\hfill \end{array}}$   Megoldás. $a)$ Euler-vonala a $B$ és $C$ gráfoknak, Euler-köre csak a $B$ gráfnak van. $b)$ Ha $\text{R=0}$, akkor a második oszlopot vizsgálva, vagy $\text{R+A=R}$ és $\text{A=0}$, de ez nem lehet, mert különböző betűk különböző számokat jelölnek, vagy $\text{R+A+1=R+10}$, ami azt jelenti, hogy $\text{A=9}$. Ekkor viszont az első oszlopot nézve $\text{O+1=9}$, tehát $\text{O=8}$. Ebből adódóan az utolsó oszlopban $\text{L+8=9}$ (más eset nincs), tehát $\text{L=1}$. Végül könnyen látható, hogy $\text{M=2}$. Vagyis: ${\displaystyle \begin{array}{ccccc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{8}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{8}}\hfill & \hfill {\displaystyle \text{1}}\hfill \\ \hfill {\displaystyle \text{ +}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{9}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{8}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{9}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{9 }}\hfill \end{array}}$   2. Egy derékszögű háromszög két csúcsa $A\left(7;1\right)$, $B\left(7;7\right)$. Hol lehet a háromszög harmadik csúcsa, ha körülírt köre áthalad az origón? Írjuk fel ennek a körnek az egyenletét.   Megoldás. Az $AB$ szakasz felező merőlegesének egyenlete: $y=4$.     Az $OA$ szakasz felező merőlegesének egyenlete: $7x+y=25$. Metszéspontjuk, vagyis a köré írt kör középpontja: $P\left(3;4\right)$. A $P$ pont nem illeszkedik az $AB$ szakaszra, az tehát nem átmérő. A $C$ pontok az $A$-nak és a $B$-nek a $P$-re vonatkozó tükörképei: $C_1\left(-1;7\right)$, $C_2\left(-1;1\right)$. A kör sugara $OP=5$, a kör egyenlete: ${\left(x-3\right)}^2+{\left(y-4\right)}^2=25$.   3. Az ábrán látható téglalap oldalai $a$ és $1\mathrm{,}5a$. Mekkora az $a$ sugarú negyedkörlapok által fedetlenül hagyott (az ábrán sötétre színezett) terület nagysága?       Megoldás. Tudjuk, hogy $AD=a$, és $AB=1\mathrm{,}5a$, tehát $AT=0\mathrm{,}75a$, $AM=a$. Az $MAT$ háromszögből a koszinusz szögfüggvény segítségével $MAT\approx 41\mathrm{,}{4}^{\circ }$. Ebből adódóan $MAD\approx 48\mathrm{,}{6}^{\circ }$. Az $MAT$ háromszögből a Pitagorasz-tétel segítségével: $MT\approx 0\mathrm{,}6614a$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{DMC}}& {\displaystyle =T_{ABCD}-T_{AMB}-2\cdot T_{AMD}\mathrm{.}}\hfill \\ \hfill {\displaystyle T_{ABCD}}& {\displaystyle =1\mathrm{,}5a^2\mathrm{,}{T}_{AMB}=\frac{AB\cdot MT}{2}\approx 0\mathrm{,}4961a^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\cdot T_{AMD}}& {\displaystyle =2\cdot \frac{48\mathrm{,}6}{360}\cdot a^2\pi \approx 0\mathrm{,}8482a^2\mathrm{,}{T}_{DMC}\approx 0\mathrm{,}1557a^2\mathrm{.}}\hfill \end{array}}$     4. Sík terepen $A$ és $B$ megközelíthetetlen tereppontok távolságát kell meghatároznunk. Ezért kitűzünk egy $C$ pontot, ahonnan a keresett távolságot ${60}^{\circ }$-os szög alatt látjuk. A ${60}^{\circ }$-os szög felező egyenesén $50\text{m}$-t megtéve, az $AB$ szakasztól távolodva a $D$ pontba jutunk. Innen az $A$ pontba mutató irány ${20}^{\circ }$-os szöget, a $B$ pontba mutató irány ${10}^{\circ }$-os szöget alkot az általunk megtett útszakasszal. Mekkora az $AB$ távolság?   Megoldás. Az $ACD\sphericalangle =BCD\sphericalangle ={150}^{\circ }$, mivel kiegészítő szögeik 30${}^{\circ }$-osak. Ebből adódóan $CAD\sphericalangle ={10}^{\circ }$ és $CBD\sphericalangle ={20}^{\circ }$. Az $ACD$ háromszögben szinusztétellel: $AD\approx 143\mathrm{,}97$ m. A $BCD$ háromszögben szinusztétellel: $BD\approx 73\mathrm{,}10$ m. Az $ABD$ háromszögben koszinusztétellel: $AB\approx 88\mathrm{,}56$ m.   II. rész   5. $a)$ Rendezzük nagyság szerint növekedő sorrendbe azokat a $k$ számokat, amelyekre teljesül, hogy $\begin{array}{c}{\displaystyle 7\mid k^3+9k^2+23k+15.}\end{array}$ Mennyi az így kapott sorozat első $100$ elemének az összege? $b)$ Legyen $a>1$. Határozzuk meg a következő kifejezés értékét: $a^{\frac{\text{lg}{a}^{\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}}}{\text{lg}a}}$.   Megoldás. $a)$ A $k^3+9k^2+23k+15$ polinomot megvizsgálva látható, hogy $k=-1$ gyöke. A $k+1$ polinommal elosztva a $k^2+8k+15$ polinom adódik, amely felírható $\left(k+3\right)\left(k+5\right)$ alakban. A $k^3+9k^2+23k+15$ polinom tehát átírható $\left(k+1\right)\left(k+3\right)\left(k+5\right)$ alakúra. Ha az eredeti kifejezés osztható 7-tel, akkor A keresett összeg a számtani sorozat összegképlete alapján határozható meg: $\begin{array}{c}{\displaystyle \frac{2\cdot 6+32\cdot 7}{2}\cdot 33+\frac{2\cdot 4+32\cdot 7}{2}\cdot 33+\frac{2\cdot 2+33\cdot 7}{2}\cdot 34=3894+3828+3995=11717.}\end{array}$ $b)$ Vizsgáljuk meg először $a^{\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}}$ kifejezés értékét $a>1$ esetén: $a^{\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}}=x$. Vehetjük mindkét oldal 10-es alapú logaritmusát, hiszen egy pozitív valós szám hatványa csak pozitív lehet: $\text{lg}{a}^{\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}}=\text{lg}x$, $\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}\text{lg}a=\text{lg}x$, $\text{lg}\left(\text{lg}a\right)=\text{lg}x$, a logaritmus függvény kölcsönösen egyértelmű: $\text{lg}a=x$. Most meg kell határozni az $a^{\frac{\text{lg}x}{\text{lg}a}}$ értékét. Behelyettesítve $x$ értékét: $a^{\frac{\text{lg}\left(\text{lg}a\right)}{\text{lg}a}}$ adódik, amiről már tudjuk, hogy $\text{lg}a$.   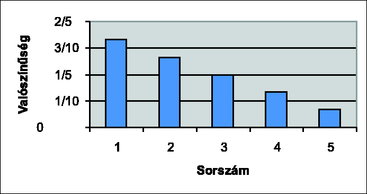6. Egy dobozban $4$ piros és $2$ sárga golyó van. Visszatevés nélkül húzunk addig, amíg az első sárga golyót kihúzzuk. A kísérlet kimenetele az ehhez szükséges húzások száma. Ábrázoljuk az így definiált valószínűségi változó eloszlását, illetve számoljuk ki a várható értékét.   Megoldás. Jelölje az első sárga húzás sorszámát $x$, ennek valószínűségét pedig $P\left(x\right)$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(1\right)}& {\displaystyle =\frac{2}{6}=\frac{5}{15}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(2\right)}& {\displaystyle =\frac{4}{6}\cdot \frac{2}{5}=\frac{4}{15}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(3\right)}& {\displaystyle =\frac{4}{6}\cdot \frac{3}{5}\cdot \frac{2}{4}=\frac{3}{15}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(4\right)}& {\displaystyle =\frac{4}{6}\cdot \frac{3}{5}\cdot \frac{2}{4}\cdot \frac{2}{3}=\frac{2}{15}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(5\right)}& {\displaystyle =\frac{4}{6}\cdot \frac{3}{5}\cdot \frac{2}{4}\cdot \frac{1}{3}=\frac{1}{15}\mathrm{.}}\hfill \end{array}}$ A várható érték: $\begin{array}{c}{\displaystyle E\left(x\right)=1\cdot \frac{5}{15}+2\cdot \frac{4}{15}+3\cdot \frac{3}{15}+4\cdot \frac{2}{15}+5\cdot \frac{1}{15}=\frac{35}{15}=\frac{7}{3}\mathrm{.}}\end{array}$     7. Az 1 dm átmérőjű félkörbe az ábrán látható módon újabb félköröket írunk. Mennyi a második félkör területe és kerülete? Milyen sorozatot határoznak meg a félkörök kerületei és területei? Véges értéket kapunk-e, ha összeadjuk az így keletkeztetett végtelen sok félkör területét? Ha igen, akkor mennyi ez az összeg?     Megoldás. Legyen $OB=OD=r_0$ és $TD=TO=r_1$. A további beírt félkörök sugarának jelölése: $r_2\mathrm{,}{r}_3\mathrm{,}{r}_4\mathrm{,}\text{...}$ legyen. $TDO$ háromszögből Pitagorasz tételével $r_1=r_0\frac{\sqrt[]{2}}{2}$, hasonlóan az $i$-edik félkörre $r_i=r_{i-1}\cdot \frac{\sqrt[]{2}}{2}$.     A második félkör kerülete: $K_1=2r_1+r_1\pi =\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{4}\pi$. A második félkör területe: $\begin{array}{c}{\displaystyle T_1=\frac{r_1{}^2\pi }{2}={\left(\frac{\sqrt[]{2}}{4}\right)}^2\pi \cdot \frac{1}{2}=\frac{\pi }{16}\mathrm{.}}\end{array}$ A kerületek mértani sorozatot alkotnak, ahol $q=\frac{\sqrt[]{2}}{2}$ ($K_i=\frac{\sqrt[]{2}}{2}{K}_{i-1}$ könnyen belátható). A területek mértani sorozatot alkotnak, ahol $q=\frac{1}{2}$ ($T_i=\frac{1}{2}{T}_{i-1}$, ez könnyen belátható). A területek sorozatából képzett mértani sor konvergens, hiszen $q=0\mathrm{,}5$, tehát véges a területek összege. $\begin{array}{c}{\displaystyle S=\frac{T_0}{1-q}=\frac{\frac{\pi }{8}}{1-\frac{1}{2}}=\frac{\pi }{8}\cdot 2=\frac{\pi }{4}\mathrm{.}}\end{array}$   8. Tekintsük a valós számokon értelmezett következő függvényt: $\begin{array}{c}{\displaystyle x\mapsto x^3+4x^2+5x\mathrm{.}}\end{array}$ $a)$ Határozzuk meg a függvény zérushelyeit. $b)$ Van-e a függvénynek lokális szélsőértéke? Ha van, akkor határozzuk meg. $c)$ Jellemezzük a függvényt növekedés és fogyás szempontjából. $d)$ Van-e a függvénynek inflexiós pontja? Ha van, akkor határozzuk meg. $e)$ Írjuk fel a függvény érintőjének egyenletét a $0$ abszcisszájú pontjában.   Megoldás. $a)$ A függvény zérushelyeit az $x^3+4x^2+5x=0$ egyenlet megoldása adja. Szorzattá alakítva a bal oldalt az $x\left(x^2+4x+5\right)$ alakot kapjuk. A zérushelyre csak az $x=0$ adódik. $b)$‐$c)$ A függvény deriváltja: $f\text{'}=3x^2+8x+5$, ennek zérushelyei $x_1=-\frac{10}{6}$ és $x_2=-1$.   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>10</mn></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>10</mn></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>10</mn></mrow><mrow><mn>6</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi></math>}}\hfill & \hfill {\displaystyle \text{nő}}\hfill & \hfill {\displaystyle \text{maximum}}\hfill & \hfill {\displaystyle \text{csökken}}\hfill & \hfill {\displaystyle \text{minimum}}\hfill & \hfill {\displaystyle \text{nő}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo></math>}}\hfill & \hfill {\displaystyle \text{+}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{+}}\hfill \\ \hline\end{array}}$     A táblázatból látható, hogy $M_1\left(-\frac{10}{6};-\frac{50}{27}\right)$ lokális maximum, az $M_2\left(-1;-2\right)$ lokális minimum. $d)$ A függvény második deriváltja $f\text{'}\text{'}=6x+8$, ennek zérushelye $x=-\frac{4}{3}$.   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi></math>}}\hfill & \hfill {\displaystyle \text{konkáv}}\hfill & \hfill {\displaystyle \text{Inflexiós pont}}\hfill & \hfill {\displaystyle \text{konvex}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo><mo stretchy="false">'</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{+}}\hfill \\ \hline\end{array}}$   $e)$ Mivel $x=0$ zérushely, ezért a függvény képe az origón, tehát a $P_0\left(0;0\right)$ ponton halad át. Az érintő iránytangensét $f\text{'}\left(0\right)=5$ adja. Az érintő egyenlete: $y=5x$.   9. A táblázat nyolc ország adatait tartalmazza. $a)$ Állítsuk növekvő sorrendbe az egyes országokat népsűrűség szerint. $b)$ Melyik országban a legnagyobb a valószínűsége annak, hogy egy állampolgár fővárosi? $c)$ Hányféleképpen tudunk kiválasztani az itt felsorolt országok közül négyet úgy, hogy pontosan két európai és pontosan két ázsiai legyen köztük? $d)$ Tekintsük ezen országok lakosságát egy számsokaság elemeinek. Mennyi ennek a számsokaságnak a terjedelme és az átlaga? ${\displaystyle \begin{array}{|ccccc|}\hline {\displaystyle \text{Ország}}\hfill & \hfill {\displaystyle \text{Terület (km<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">)</mo></math>}}& \hfill {\displaystyle \text{Lakosok száma (fő)}}& \multicolumn{1}{c}{{\displaystyle \text{Főváros}}}& \multicolumn{1}{c}{{\displaystyle \text{Főváros}}}\\ {\displaystyle }\hfill & \hfill {\displaystyle }& \hfill {\displaystyle }& {\displaystyle }\hfill & \hfill {\displaystyle \text{lakossága (fő)}}\\ {\displaystyle \text{Ausztrália}}\hfill & \hfill {\displaystyle \text{7 682 300}}& \hfill {\displaystyle \text{17 483 000}}& {\displaystyle \text{Canberra}}\hfill & \hfill {\displaystyle \text{197 000}}\\ {\displaystyle \text{Banglades}}\hfill & \hfill {\displaystyle \text{147 570}}& \hfill {\displaystyle \text{111 400 000}}& {\displaystyle \text{Dhaka}}\hfill & \hfill {\displaystyle \text{3 683 000}}\\ {\displaystyle \text{Hollandia}}\hfill & \hfill {\displaystyle \text{33 939}}& \hfill {\displaystyle \text{15 298 000}}& {\displaystyle \text{Amszterdam}}\hfill & \hfill {\displaystyle \text{720 000}}\\ {\displaystyle \text{India}}\hfill & \hfill {\displaystyle \text{3 287 263}}& \hfill {\displaystyle \text{846 303 000}}& {\displaystyle \text{Új Delhi}}\hfill & \hfill {\displaystyle \text{273 000}}\\ {\displaystyle \text{Kína}}\hfill & \hfill {\displaystyle \text{9 608 378}}& \hfill {\displaystyle \text{1 198 340 000}}& {\displaystyle \text{Peking}}\hfill & \hfill {\displaystyle \text{7 000 000}}\\ {\displaystyle \text{Magyarország}}\hfill & \hfill {\displaystyle \text{93 036}}& \hfill {\displaystyle \text{10 310 000}}& {\displaystyle \text{Budapest}}\hfill & \hfill {\displaystyle \text{1 992 000}}\\ {\displaystyle \text{Málta}}\hfill & \hfill {\displaystyle \text{316}}& \hfill {\displaystyle \text{362 000}}& {\displaystyle \text{Valletta}}\hfill & \hfill {\displaystyle \text{9210}}\\ {\displaystyle \text{Mongólia}}\hfill & \hfill {\displaystyle \text{1 565 500}}& \hfill {\displaystyle \text{2 250 000}}& {\displaystyle \text{Ulánbátor}}\hfill & \hfill {\displaystyle \text{619 000}}\\ \hline\end{array}}$   Megoldás. $a)$ Az országok sorrendje népsűrűség (fő/km${}^2)$ szerint Mongólia (1,44); Ausztrália (2,276); Magyarország (110,82); Kína (124,72); India (257,45); Hollandia (450,75); Banglades (754,896); Málta (1145,57). $b)$ Mongólia (27,51%). $c)$ $\left(\genfrac{}{}{0ex}{}{3}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)=18$-féleképpen. $d)$ Terjedelem: $1198340000-362000=1197978000$. Az átlag: 275 218 250.