Cím:	Megoldásvázlatok a 2005/4. sz. I. emelt szintű gyakorló feladataihoz
Szerző(k):	Kántor Sándor
Füzet:	2005/áprilisi melléklet, 58 - 63. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor
Hivatkozás(ok):	2005/extra1: Emelt szintű gyakorló feladatsor I.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Határozza meg az $a$ és $b$ pozitív egész számok lehetséges értékeit, ha $a<b$, továbbá teljesül, hogy ha $x$ és $y$ eleme az $\left[a;b\right]$ intervallumnak, akkor $\frac{1}{x}+\frac{1}{y}$ is eleme $\left[a;b\right]$-nek!  (12 pont)   Megoldás. Nem lehet $a>1$, mert akkor $a\ge 2$ miatt $x\ge 2$ és $y\ge 2$ lenne, és így $\frac{1}{x}+\frac{1}{y}\le \frac{1}{2}+\frac{1}{2}=1$ lenne, ami ellenkezik $\frac{1}{x}+\frac{1}{y}\ge a\ge 2$-vel. Tehát $a=1$. A $b$ értéke csak 2 lehet, mert egyrészt $b>a$ miatt $b\ge 2$, másrészt $b>2$ nem lehet. Ugyanis $b>2$ esetén $x=2\mathrm{,}5$ és $y=2\mathrm{,}5$ az $\left[a;b\right]$ eleme, de $\begin{array}{c}{\displaystyle \frac{1}{2\mathrm{,}5}+\frac{1}{2\mathrm{,}5}=0\mathrm{,}8<1=a}\end{array}$ miatt $\frac{1}{x}+\frac{1}{y}$ nem eleme $\left[a;b\right]$-nek. Az $a=1$, $b=2$ jó, mert $1\le x\le 2$ és $1\le y\le 2$ esetén $1\le \frac{1}{x}+\frac{1}{y}\le 2$. Tehát a keresett számok: $a=1$ és $b=2$.   2. $a)$ Oldja meg a valós számok halmazán a $\begin{array}{c}{\displaystyle \sqrt[]{1+x\sqrt[]{x^2-16}}=x-1}\end{array}$ egyenletet!  (5 pont) $b)$ Adja meg a fenti egyenlet alaphalmazát!  (7 pont)   Megoldás. Ha van az egyenletet kielégítő $x$, akkor az egyenlet két oldalának négyzete is egyenlő: $\begin{array}{c}{\displaystyle 1+x\sqrt[]{x^2-16}=x^2-2x+\mathrm{1,}\text{ azaz }x\sqrt[]{x^2-16}=x^2-2x\mathrm{.}}\end{array}$ Az eredeti egyenletnek $x=0$ nem megoldása, tehát a megoldásra $\sqrt[]{x^2-16}=x-2$ is, így $x^2-16=x^2-4x+4$ is teljesül, ezért a megoldás csak $x=5$ lehet. Behelyettesítés mutatja, hogy ez valóban megoldás is. $b)$ Az alaphalmaz azokból az $x$ valós számokból áll, amelyekre egyrészt $x^2-16\ge 0$, és így $|x|\ge 4$ is, másrészt $x\sqrt[]{x^2-16}\ge -1$ is teljesül. Ez utóbbi nemnegatív $x$-re mindig teljesül. Negatív $x$-re pedig pontosan akkor, ha $|x|\sqrt[]{x^2-16}\le 1$, azaz ha $x^4-16x^2-1\le 0$. $x^4-16x^2-1\le 0$ megoldásai a $8-\sqrt[]{65}\le x^2\le 8+\sqrt[]{65}$ egyenlőtlenséget teljesítő $x$ értékek, tehát azok, amelyekre $-\sqrt[]{8+\sqrt[]{65}}\le x\le \sqrt[]{8+\sqrt[]{65}}$ teljesül. Ezek közül a negatívok: $-\sqrt[]{8+\sqrt[]{65}}\le x<0$. Tehát a keresett alaphalmaz: $\begin{array}{c}{\displaystyle \left[-\sqrt[]{8+\sqrt[]{65}};-4\right]\cup \left[4;\infty \right)\mathrm{.}}\end{array}$   3. Egy autókereskedő ötfajta autót forgalmaz. Az egyes fajták darabját $\begin{array}{c}{\displaystyle 2\mathrm{,}32\mathrm{,}833\mathrm{,}13\mathrm{,}5}\end{array}$ MFt-ért adja el, és nyeresége (az eladási ár és a beszerzési ár különbsége) fajtánként a fenti sorrendben az eladási ár $\begin{array}{c}{\displaystyle 32\mathrm{,}52\mathrm{,}42\mathrm{,}12}\end{array}$ százaléka. Ez a két adatsor a további vizsgálatok során nem változik. Az egyes fajtákból (fenti sorrendben) ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{2003-ban}}& {\displaystyle 2532273819\text{darabot,}}\hfill \\ \hfill {\displaystyle \text{2004-ben}}& {\displaystyle 2731293233\text{darabot}}\hfill \end{array}}$ adott el. $a)$ Mennyi volt a nyeresége 2003-ban, és mennyi 2004-ben?  (5 pont) $b)$ Ha 2005-ben csak egy autófajtát forgalmaz, akkor melyik autófajtát (mennyi annak az egységára) érdemes forgalmaznia, és abból legalább hányat kell eladnia, ha a lehető legkevesebb autó eladásával akarja elérni a 2004-es nyereségét?  (7 pont)   Megoldás. $a)$ A nyereség 2003-ban: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 2\mathrm{,}3\cdot 0\mathrm{,}03\cdot 25+2\mathrm{,}8\cdot 0\mathrm{,}025\cdot 32+3\cdot 0\mathrm{,}024\cdot 27+3\mathrm{,}1\cdot 0\mathrm{,}021\cdot 38+3\mathrm{,}5\cdot 0\mathrm{,}02\cdot 19=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =9\mathrm{,}7128\text{(MFt). }}\hfill \end{array}}$ A nyereség 2004-ben: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 2\mathrm{,}3\cdot 0\mathrm{,}03\cdot 27+2\mathrm{,}8\cdot 0\mathrm{,}025\cdot 31+3\cdot 0\mathrm{,}024\cdot 29+3\mathrm{,}1\cdot 0\mathrm{,}021\cdot 32+3\mathrm{,}5\cdot 0\mathrm{,}02\cdot 33=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =10\mathrm{,}5142\text{(MFt). }}\hfill \end{array}}$ $b)$ A legnagyobb nyereség egy autó eladásánál annál az autófajtánál van, amelynél az eladási ár százalékértéke a legnagyobb. Ezek a százalékértékek rendre ${\displaystyle \begin{array}{cccccc}\hfill {\displaystyle 2\mathrm{,}3\cdot 0\mathrm{,}03}& {\displaystyle =0\mathrm{,}069;}\hfill & {\displaystyle 2\mathrm{,}8\cdot 0\mathrm{,}025}\hfill & \hfill {\displaystyle =0\mathrm{,}07;}& {\displaystyle }\hfill & {\displaystyle 3\cdot 0\mathrm{,}024=0\mathrm{,}072;}\hfill \\ \hfill {\displaystyle 3\mathrm{,}1\cdot 0\mathrm{,}021}& {\displaystyle =0\mathrm{,}0651;}\hfill & {\displaystyle 3\mathrm{,}5\cdot 0\mathrm{,}02}\hfill & \hfill {\displaystyle =0\mathrm{,}\mathrm{07,}}\end{array}}$ így a legnagyobb százalékérték (a 0,072) a 3 MFt árú autófajtánál van. Ebből az autófajtából legalább annyit kell eladnia, amennyivel a nyereség először nagyobb vagy egyenlő a 2004-es nyereségnél. Ez a szám: $\begin{array}{c}{\displaystyle \frac{10\mathrm{,}5142}{0\mathrm{,}072}=146\mathrm{,}03055\text{...}}\end{array}$ miatt 147.   4. Az $r$ és az $R$ sugarú körök kívülről érintik egymást, és $r<R$. Közös külső érintőik szöge $\alpha$. $a)$ Mennyi $\frac{R}{r}$, ha $\alpha ={60}^{\circ }$?  (5 pont) $b)$ Mennyi $\alpha$, ha $\frac{R}{r}=\frac{5}{3}$?  (5 pont) $c)$ Mennyi annak a négyszögnek a területe, amelynek két csúcsa a körök középpontja, további két csúcsa pedig az egyik közös külső érintőn levő két érintési pont, ha $R=5$ és $r=3$?  (5 pont)   Megoldás. $a)$ A $c)$ részben említett négyszögben az egyik szárral párhuzamosan és a másik szár végpontján át húzott egyenes olyan $O_1{B}_1{O}_2$ derékszögű háromszöget jelöl ki, amelyből $\begin{array}{c}{\displaystyle \frac{R-r}{R+r}=\text{sin}{30}^{\circ }=\frac{1}{2}\mathrm{.}}\end{array}$ Ebből $\frac{R}{r}=3$.     $b)$ A fenti egyenletet kissé átrendezve: $\begin{array}{c}{\displaystyle \frac{\frac{R}{r}-1}{\frac{R}{r}+1}=\text{sin}\frac{\alpha }{2}\mathrm{.}}\end{array}$ Ebből $\text{sin}\frac{\alpha }{2}=\frac{1}{4}$, így a keresett érték: $\alpha \approx {29}^{\circ }$. $c)$ A kérdéses négyszög olyan derékszögű trapéz, amelynek alapjai $R$ és $r$, az ezekre merőleges szár a már említett derékszögű háromszögből Pitagorasz tételével számítható: $\begin{array}{c}{\displaystyle m=\sqrt[]{{\left(R+r\right)}^2-{\left(R-r\right)}^2}=2\sqrt[]{Rr}\mathrm{.}}\end{array}$ A keresett terület az adott sugárértékekkel: $\begin{array}{c}{\displaystyle \frac{5+3}{2}\cdot 2\sqrt[]{5\cdot 3}=8\sqrt[]{15}\approx 30\mathrm{,}98.}\end{array}$   II. rész   5. A $H$ halmaz a $2005$-nél nem nagyobb pozitív egész számok halmazának olyan részhalmaza, hogy tetszőleges két elemének összege nem osztható hárommal. Legfeljebb hány eleme van ennek a $H$ halmaznak?  (14 pont)   Megoldás. Vizsgáljuk a 2005-nél nem nagyobb pozitív egész számokat a hárommal való osztási maradékaik szerint. Az olyan számokból, amelyeknek az osztási maradéka 0, csak egy szerepelhet a $H$ halmazban, mert két ilyen szám összege osztható hárommal. Ha 1, vagy ha 2 az osztási maradék, akkor csak az egyik fajta szerepelhet $H$-ban, mert különböző fajták összege osztható hárommal. Egy fajtából viszont akármennyi lehet, és a 0 maradékot adó szám is ott lehet közöttük. A kérdés most már csak az, hogy melyik fajtából van több az adott halmazunkban. 2004 osztható hárommal, így 1-től 2004-ig ugyanannyi szám ad 1 maradékot, mint ahány 2 maradékot, és a számuk 668. Mivel 2005 maradéka 1, azért az 1 maradékot adókat és egy 0 maradékot adót választva a $H$ halmazba, maximális elemszám érhető el, és ez a szám 670.   6. Egy dobozban öt piros golyó van. $a)$ Hány fehér golyót kell a dobozba tennünk, ha azt akarjuk, hogy ezután a dobozból a golyók közül egyet véletlenszerűen kihúzva (a golyók kihúzásának valószínűsége megegyezik) a kihúzott golyó $0\mathrm{,}25$ valószínűséggel piros legyen?  (6 pont) $b)$ Legalább hány fehér és legalább hány fekete golyót kell a dobozba tennünk (mindegyikből legalább egyet teszünk), ha azt akarjuk, hogy ezután a dobozból a golyók közül egyet véletlenszerűen kihúzva, a kihúzott golyó $0\mathrm{,}25$ valószínűséggel ne fekete legyen?  (10 pont)   Megoldás. $a)$ Ha $x$ darab fehér golyót teszünk a dobozba, akkor $\frac{5}{5+x}$ a valószínűsége annak, hogy a kihúzott golyó piros lesz. Az $\frac{5}{5+x}=0\mathrm{,}25$ egyenlet megoldása $x=15$, tehát a keresett szám 15. $b)$ Ha $x$ darab fehér és $y$ darab fekete golyót teszünk a dobozba, akkor $\frac{5+x}{5+x+y}$ a valószínűsége annak, hogy a kihúzott golyó piros vagy fehér lesz, tehát nem lesz fekete. Az $\begin{array}{c}{\displaystyle \frac{5+x}{5+x+y}=0\mathrm{,}25}\end{array}$ egyenlet átrendezve ($x$ és $y$ nem negatívok, a nevező nem 0): $y=3x+15$. Tehát a keresett számok: $x=1$,  $y=18$.   7. Oldja meg a valós számok halmazán az $\begin{array}{c}{\displaystyle \text{log}{}_x\left(x^2+x-4\right)<1}\end{array}$ egyenlőtlenséget!  (16 pont)   Megoldás. Nyilvánvaló, hogy a logaritmus alapja miatt csak a pozitív $x$ értékek jöhetnek számításba. Teljesülni kell $x^2+x-4>0$-nak is, ami $\begin{array}{c}{\displaystyle x<\frac{1}{2}\left(-1-\sqrt[]{17}\right)\mathrm{,}\text{ valamint }x>\frac{1}{2}\left(-1+\sqrt[]{17}\right)}\end{array}$ esetén igaz. Ez és $x>0$ akkor teljesül, ha $x>\frac{1}{2}\left(-1+\sqrt[]{17}\right)$. Ekkor az alapszám 1-nél nagyobb, és ilyen alapszám esetén a logaritmus pontosan akkor kisebb 1-nél, ha a logaritmálandó mennyiség kisebb az alapszámnál, tehát a mi esetünkben, ha $x^2+x-4<x$. Ez $-2<x<2$ esetén teljesül, tehát a feladat megoldása $\frac{1}{2}\left(\sqrt[]{17}-1\right)<x<2$.   8. Legyen $A$ az a háromoldalú egyenes hasáb, amelynek alaplapja $2$ oldalhosszúságú szabályos háromszög és oldalélének hossza is $2$. Az egyik oldallapjának középpontján áthaladó, a lapra merőleges egyenes körül forgassuk el az $A$ testet ${90}^{\circ }$-kal, és jelöljük $A\text{'}$-vel az elforgatott testet! Mennyi az $A\cup A\text{'}$ test $a)$ térfogata?  (8 pont) $b)$ felszíne?  (8 pont) 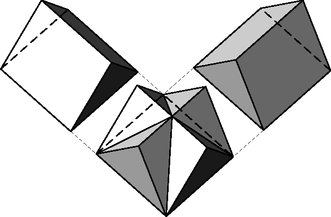  Megoldás. Könnyű belátni, hogy $A\cap A\text{'}$ olyan négyoldalú egyenes gúla, amelynek alapja a közös oldallap, magassága a hasáb alaplapjának magassága.     $a)$ $A\cap A\text{'}$ térfogata: $\begin{array}{c}{\displaystyle 2\cdot 2\cdot \sqrt[]{3}\cdot \frac{1}{3}=\frac{4\sqrt[]{3}}{3}\approx \mathrm{2,31.}}\end{array}$ $A\cup A\text{'}$ térfogata: $\begin{array}{c}{\displaystyle 2\cdot \sqrt[]{3}\cdot 2-\frac{4\sqrt[]{3}}{3}=\frac{8\sqrt[]{3}}{3}\approx \mathrm{4,62.}}\end{array}$ $b)$ $A\cup A\text{'}$ felszínének meghatározásához elegendő azt észrevenni, hogy ez a felszín az $A$ felszínénél a hasáb két párhuzamos lapjának területével nagyobb, mert egy oldallap közös, két-két oldallap megmaradó része pedig együtt adja ki $A$ két oldallapját. Tehát a keresett felszín: $3\cdot 4+4\cdot \sqrt[]{3}\approx 18\mathrm{,}93$.   9. $a)$ Írja fel azoknak a paraboláknak az egyenletét, amelyek grafikonja a $P\left(1;0\right)$ pontban érinti az $y=2-2x$ egyenletű egyenes grafikonját, és tengelye az $y$ tengellyel párhuzamos!  (9 pont) $b)$ Hol helyezkednek el ezeknek a paraboláknak a csúcspontjai?  (9 pont)   Megoldás. $a)$ A parabolák egyenletét $y=a{x}^2+bx+c$ ($a\ne 0$) alakban keressük. Mivel a parabola illeszkedik a $P\left(1;0\right)$ pontra, $0=a+b+c$, azaz $c=-a-b$.     Az adott egyenesnek és ennek a parabolának csak egy közös pontja lehet, ezért a $\begin{array}{c}{\displaystyle 2-2x=a{x}^2+bx-a-b}\end{array}$ egyenletnek csak egy gyöke lehet. A diszkriminánsa: $\begin{array}{c}{\displaystyle {\left(b+2\right)}^2+4a\left(a+b+2\right)={\left(b+2+2a\right)}^2=\mathrm{0,}}\end{array}$ így $b=-2a-2$. A parabolák egyenlete tehát $\begin{array}{c}{\displaystyle y=a{x}^2-\left(2a+2\right)x+a+\mathrm{2,}}\end{array}$ ahol $a\in \text{R}\setminus \left\{0\right\}$. $b)$ A parabolák csúcspontját a szélsőérték helye és nagysága alapján határozzuk meg. Helye: $\frac{a+1}{a}$, nagysága: $\begin{array}{c}{\displaystyle a{\left(\frac{a+1}{a}\right)}^2-\left(2a+2\right)\frac{a+1}{a}+a+2=-\frac{1}{a}\mathrm{.}}\end{array}$ ($a\ne 0$, ezt az elején kikötöttük.) A csúcspontok paraméteres egyenlete: $x=\frac{a+1}{a}$, $y=-\frac{1}{a}$. Ez éppen az $x+y=1$ egyenletű egyenes, ahol az $x\ne 1$, $y\ne 0$, tehát a $P$ pont kivételével. A csúcspontok tehát ezen az egyenesen vannak, és nyilvánvaló (bár ezt nem kérdezte a feladat), hogy az egyenes pontjai $P$ kivételével csúcspontok.