Cím:	Megoldásvázlatok a 2004/8. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Meszlényiné Róka Ágnes
Füzet:	2004/december, 533 - 536. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Oldjuk meg az $\begin{array}{c}{\displaystyle x\cdot {\left(\frac{x-3}{3}\right)}^2+\frac{1}{3}\left(x-2\right)\left(x+2\right)=\frac{1+{\left(x-1\right)}^3}{9}}\end{array}$ egyenletet.   Megoldás. Azonos átalakítások és az egyenlet rendezése után elsőfokú egyenletet kapunk. Megoldása: $x=2$.   2. Egy kockával $6$-szor dobunk egymás után és feljegyezzük az eredményeket. $a)$ Hányféle sorozat jöhet létre? $b)$ Hányféle sorozat jöhet létre, ha az első helyen és csak ezen áll $1$-es? $c)$ Mennyi a valószínűsége annak, hogy az első helyen a többitől különböző szám áll?   Megoldás. $a)$ Az összes eset: $6^6=46656$. $b)$ Az első hely kötött, itt van az 1-es. A következő öt hely mindegyikén az öt szám bármelyike állhat, azaz $5^5=3125$ eset van. $c)$ A kedvező esetek száma az előző megfontolást követve: $6\cdot 5^5$. Így a kérdéses valószínűség: $\begin{array}{c}{\displaystyle P=\frac{6\cdot 5^5}{6^6}=\frac{5^5}{6^5}\approx 0\mathrm{,}402.}\end{array}$   3. Egy matematika tanár akkor mondja, hogy szerencsésen állította össze a dolgozatot, ha a jegyek átlaga $e$ és $\pi$ között van $(e=2\mathrm{,}718\text{...}$ és $\pi =3\mathrm{,}141\text{...})$. Egy $35$ fős osztályból a legjobb gyerek munkáját még nem nézte meg, és ekkor az átlag $2\mathrm{,}68$ volt. Hogyan sikerülhetett a legjobb tanuló dolgozata, ha a tanár elmondhatta magáról, hogy szerencsésen állította össze a dolgozatot?   Megoldás. Mivel a 34 gyerek dolgozatának átlaga 2,68 és ez kerekített érték, azért a jegyeik $S$ összege $\begin{array}{c}{\displaystyle 2\mathrm{,}675\cdot 34=90\mathrm{,}95\le S<2\mathrm{,}685\cdot 34=91\mathrm{,}29.}\end{array}$ A jegyek összege tehát 91. Legyen a legjobb tanuló osztályzata $n$, ahol $n$ lehetséges értékei: 1, 2, 3, 4, 5. A megoldandó egyenlőtlenség: $\begin{array}{c}{\displaystyle 2\mathrm{,}718\le \frac{91+n}{35}\le 3\mathrm{,}\mathrm{141,}}\end{array}$ amelynek az öt lehetséges érték közül csak az $n=5$ tesz eleget. A legjobb tanuló 5-ös dolgozatot írt; az átlag ebben az esetben 2,74 volt. 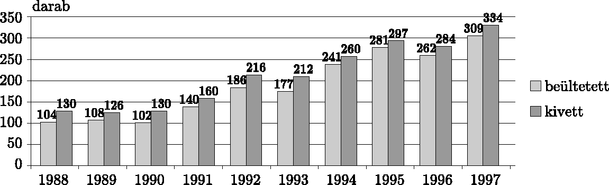  4. Tekintsük a következő diagramot. Egy $10$ éves periódusban a beültetett és a kivett vesék darabszámát olvashatjuk le róla.     $a)$ Melyik évben ültették be a legnagyobb százalékban a kivett veséket? $b)$ Ábrázoljuk az első és az utolsó három évben a beültetett és a kivett vesék arányát. $c)$ Levonható-e valamilyen következtetés a kapott ábráról?   Megoldás. $a)$ Készítsük el a következő táblázatot: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cccccccccc|}\hline \hfill {\displaystyle \text{1988.}}\hfill & \hfill {\displaystyle \text{1989.}}\hfill & \hfill {\displaystyle \text{1990.}}\hfill & \hfill {\displaystyle \text{1991.}}\hfill & \hfill {\displaystyle \text{1992.}}\hfill & \hfill {\displaystyle \text{1993.}}\hfill & \hfill {\displaystyle \text{1994.}}\hfill & \hfill {\displaystyle \text{1995.}}\hfill & \hfill {\displaystyle \text{1996.}}\hfill & \hfill {\displaystyle \text{1997.}}\hfill \\ \hfill {\displaystyle \text{80\%}}\hfill & \hfill {\displaystyle \text{85,7\%}}\hfill & \hfill {\displaystyle \text{78,5\%}}\hfill & \hfill {\displaystyle \text{87,5\%}}\hfill & \hfill {\displaystyle \text{86,1\%}}\hfill & \hfill {\displaystyle \text{83,5\%}}\hfill & \hfill {\displaystyle \text{92,7\%}}\hfill & \hfill {\displaystyle \text{94,6\%}}\hfill & \hfill {\displaystyle \text{92,3\%}}\hfill & \hfill {\displaystyle \text{92,5\%}}\hfill \\ \hline\end{array}}}\end{array}$ A táblázat mutatja, hogy 1995-ben ültették be a legnagyobb százalékban a kivett veséket. $b)$ Ha a függőleges tengely beosztását tized pontossággal készítjük el, akkor a kért évekhez tartozó 0,8; 0,86; 0,79 és 0,95; 0,92; 0,93 arányokat például oszlopdiagramon tudjuk ábrázolni. $c)$ Látható, hogy az arány a vizsgált időszak utolsó három évében magasabb, mint az első három évben volt. (Valószínű, hogy fejlődött a kivételhez és a kivett vesék szállításához, eltartásához szükséges műszerezettsége a kórházaknak.)   II. rész   5. Egy trapéz egyik átlója ${30}^{\circ }$-os szöget zár be az alappal. A két átló merőleges egymásra. $a)$ Milyen hosszú a két átló, ha az alapok $6$ és $4$ egység hosszúak? $b)$ Mekkora a trapéz területe? $c)$ Számítsuk ki a trapéz kerületét. 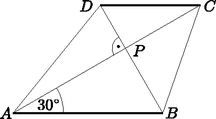  Megoldás. Készítsünk vázlatrajzot.     $a)$ $BAC\sphericalangle =DCA\sphericalangle$, mert váltószögek, így a $PAB▵$ és a $PCD▵$ is olyan derékszögű háromszög, amelynek van ${30}^{\circ }$-os és ${60}^{\circ }$-os szöge, ezért a két háromszög oldalainak a hossza meghatározható: $BP=3$, $AP=3\sqrt[]{3}$, illetve $DP=2$, $CP=2\sqrt[]{3}$. Vagyis $AC=5\sqrt[]{3}$, $BD=5$. $b)$ Mivel az átlók merőlegesek egymásra, azért a trapéz területe a szorzatuk felével egyenlő: $\begin{array}{c}{\displaystyle t=\frac{5\cdot 5\sqrt[]{3}}{2}=\frac{25}{2}\sqrt[]{3}\approx 21\mathrm{,}65\text{ (területegység).}}\end{array}$ $c)$ A kerület kiszámításához határozzuk meg a szárak hosszát! Használjuk a Pitagorasz tételt: $\begin{array}{c}{\displaystyle AD=\sqrt[]{A{P}^2+D{P}^2}=\sqrt[]{31}\approx 5\mathrm{,}\mathrm{57,}BC=\sqrt[]{B{P}^2+C{P}^2}=\sqrt[]{21}\approx 4\mathrm{,}58.}\end{array}$ A trapéz kerülete: $k\approx 6+4\mathrm{,}58+4+5\mathrm{,}57=20\mathrm{,}15$ (egység).   6. Tekintsük a valós számokon értelmezett $\begin{array}{c}{\displaystyle f\left(x\right)=13-{\left(x-1\right)}^2\text{és}g\left(x\right)=4|x+1|}\end{array}$ függvényeket. $a)$ Oldjuk meg az $f\left(x\right)\ge g\left(x\right)$ egyenlőtlenséget grafikusan. $b)$ Mekkora területű az $f\left(x\right)$ és a $g\left(x\right)$ görbéje által határolt síkidom?   Megoldás. $a)$ Az ábrázolás után a megoldás leolvasható: $-2\le x\le 2$.     $b)$ Az $f\left(x\right)$ görbéje alatti terület meghatározása: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\int }_{-2}^2\left[13-{\left(x-1\right)}^2\right]dx={\int }_{-2}^2\left(-x^2+2x+12\right)dx=}\hfill \\ \hfill {\displaystyle ={\left[-\frac{x^3}{3}+x^2+12x\right]}_{-2}^2=}\hfill \\ \hfill {\displaystyle =-\frac{8}{3}+4+24-\frac{8}{3}-4+24=\frac{128}{3}\mathrm{.}}\hfill \end{array}}$ A $g\left(x\right)$ görbéje alatti terület meghatározásakor két derékszögű háromszög területösszegének kiszámítására van szükségünk: $\frac{1\cdot 4}{2}+\frac{3\cdot 12}{2}=20$. A keresett síkidom területe: $\frac{128}{3}-20=\frac{68}{3}$ (területegység).   7. Bizonyítsuk be, hogy az $\begin{array}{c}{\displaystyle 5x^2-2\left(5k+3\right)x+5k^2+6k+1=0}\end{array}$ egyenlet gyökeinek különbsége $k$ minden értékére ugyanakkora.   Megoldás. Írjuk fel a megoldóképletet: $\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}=\frac{2\left(5k+3\right)\pm \sqrt[]{4{\left(5k+3\right)}^2-20\left(5k^2+6k+1\right)}}{10}\mathrm{.}}\end{array}$ A diszkrimináns értéke 16, így $x_1=k+1$; $x_2=k+0\mathrm{,}2$. A két gyök különbsége minden $k$ esetén 0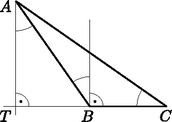,8.   8. Az $ABC$ háromszögben $\beta -\gamma ={90}^{\circ }$. Bizonyítsuk be, hogy az $A$ csúcsból induló magasság egyenese a háromszög köré írható körének érintője is egyben.   Megoldás. Készítsünk vázlatrajzot.     A feladat szövege alapján megállapítható, hogy az ábrán jelölt egyíves szögek egyenlők, mindhárom $\gamma$. Ha tekintjük a háromszög körülírt körét, akkor az $AB$ ív szempontjából a $C$-nél lévő szög kerületi szög, a $TAB\sphericalangle$ pedig érintő szárú kerületi szög. Az $ABC$ háromszög $AT$ magassága tehát a háromszög köré írható körnek az érintője is.   9. Válasszuk ki az $50\text{cm}$ kerületű, egyenlő szárú háromszögek közül azt, amelyben minimális az oldalakra rajzolható négyzetek területösszege.   Megoldás. Jelöljük a szárak hosszát $b$-vel, ekkor az alap $a=50-2b$. A kérdéses terület: $t\left(b\right)=2b^2+{\left(50-2b\right)}^2$. Ennek a másodfokú függvénynek minimuma van. A $t\left(b\right)=6b^2-200b+2500$ függvény minimumhelye: $\frac{200}{2\cdot 6}=\frac{50}{3}$. A keresett egyenlő szárú háromszög az a szabályos háromszög, melynek oldala $\frac{50}{3}$ egység.