Cím:	Megoldásvázlatok a 2004/7. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Szászné Simon Judit
Füzet:	2004/november, 463 - 467. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Határozzuk meg azon négyzet csúcspontjainak a koordinátáit, amelynek három csúcsa illeszkedik az $x^2-6x-5y+4=0$ egyenletű parabolára, és átlói párhuzamosak a koordináta-tengelyekkel. $a)$ Mekkora a négyzetbe írt kör területe? $b)$ Hány rácspontja van a zárt körlapnak?  (11 pont) 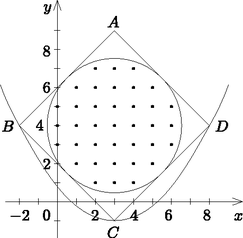  Megoldás. Az $x^2-6x-5y+4=0$ parabola egyenletét alakítsuk a következőképpen: $\begin{array}{c}{\displaystyle \frac{{\left(x-3\right)}^2}{5}=y+1.}\end{array}$ Csúcspontja leolvasható: $C\left(3;-1\right)$. A négyzet oldalegyenese ${45}^{\circ }$-os szöget zár be az $x$ tengellyel, és átmegy $C$-n, ezért egyenlete $y=x-4$. Második metszéspontja a parabolával $D\left(8;4\right)$, tehát $B\left(-2;4\right)$ és $A\left(3;9\right)$. A négyzet átlója 10 egység, így oldala $5\sqrt[]{2}$, ami a keresett kör átmérője. A négyzetbe írt kör területe $T=\frac{25\pi }{2}$. A kör egyenlete ${\left(x-3\right)}^2+{\left(y-4\right)}^2=\frac{25}{2}$.     Az $y=4$ és az $x=3$ egyeneseken a körben 13 rácspont van, egy negyedkörben még 6 újabb rácspont, tehát összesen 37 rácspont van a zárt körlapon. (Tulajdonképpen azt kell leszámolni, hányféleképpen adhat két egész szám négyzetösszege 12,5-nél kisebbet.)   2. Oldjuk meg a következő egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle 1-x^2-x^4=4^{\text{sin}{}^{2}x}\mathrm{.}}\end{array}$ (12 pont)   Megoldás. Mivel $0\le \text{sin}{}^{2}x\le 1$, azért a jobb oldal értékkészlete $1\le 4^{\text{sin}{}^{2}x}\le 4$. A bal oldal értéke legfeljebb 1 lehet, és az is csak akkor, ha $x=0$. Ez az egyetlen megoldása az egyenletnek.   3. Az alábbi táblázat a fogyasztói árindex alakulását mutatja néhány országban $1995$‐$1999$ között: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cccccc|}\hline \multicolumn{1}{c}{{\displaystyle \text{<span style="font-weight: bold;">Ország</span>}}}& \multicolumn{5}{c}{{\displaystyle \text{<span style="font-weight: bold;">változás az előző évhez képest, \%</span>}}}\\ {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1995</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1996</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1997</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1998</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1999</span>}}\hfill \\ {\displaystyle \text{Ausztria}}\hfill & \hfill {\displaystyle \text{2,3}}\hfill & \hfill {\displaystyle \text{1,5}}\hfill & \hfill {\displaystyle \text{1,3}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{0,6}}\hfill \\ {\displaystyle \text{Franciaország}}\hfill & \hfill {\displaystyle \text{1,7}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{1,2}}\hfill & \hfill {\displaystyle \text{0,8}}\hfill & \hfill {\displaystyle \text{0,6}}\hfill \\ {\displaystyle \text{Lengyelország}}\hfill & \hfill {\displaystyle \text{27,8}}\hfill & \hfill {\displaystyle \text{19,9}}\hfill & \hfill {\displaystyle \text{14,8}}\hfill & \hfill {\displaystyle \text{11,6}}\hfill & \hfill {\displaystyle \text{7,3}}\hfill \\ {\displaystyle \text{<span style="font-weight: bold;">Magyarország</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">28,2</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">23,6</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">18,3</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">14,3</span>}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">10</span>}}\hfill \\ {\displaystyle \text{Nagy-Britannia}}\hfill & \hfill {\displaystyle \text{3,4}}\hfill & \hfill {\displaystyle \text{2,4}}\hfill & \hfill {\displaystyle \text{3,2}}\hfill & \hfill {\displaystyle \text{3,4}}\hfill & \hfill {\displaystyle \text{1,6}}\hfill \\ {\displaystyle \text{Németország}}\hfill & \hfill {\displaystyle \text{1,8}}\hfill & \hfill {\displaystyle \text{1,4}}\hfill & \hfill {\displaystyle \text{1,9}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{0,6}}\hfill \\ \hline\end{array}}}\end{array}$ $a)$ Értelmezzük, mit jelent Ausztriánál az utolsó két oszlopban található $1$ és $0\mathrm{,}6$ szám. $b)$ Ha valaki $1994$-ben $34000$ forintot az ágynemű közé rejtett, hány forintnak felel meg a vásárlóereje $1999$-ben? $c)$ Nagymami $200000$ forintot akar diplomaajándékként az unokájának adni $1999$-ben, amikor végez. Mennyi pénzt tett a sikeres felvételi vizsga hírére $1994$-ben abba a bankba, amelyik ‐ mint utóbb kiderült ‐ pontosan a fogyasztói árindexszel megegyező kamatot adott $1994$ és $1999$ között?  (14 pont)   Megoldás. $a)$ Azt jelenti, hogy a fogyasztói árak átlagosan az előző évinek 1,01-; illetve 1,006-szeresei lettek. $b)$ Az 1994-es forint 1995-ben már csak az eredeti összeg $\frac{1}{1+\frac{28\mathrm{,}2}{100}}$-szorosát érte, és hasonló gondolatmenettel kiszámítható, hogy az 1994-ben elrejtett 34 000 Ft vásárlóértéke 1999-ben $\begin{array}{c}{\displaystyle 34000\cdot \frac{1}{1+\frac{28\mathrm{,}2}{100}}\cdot \frac{1}{1+\frac{23\mathrm{,}6}{100}}\cdot \frac{1}{1+\frac{18\mathrm{,}3}{100}}\cdot \frac{1}{1+\frac{14\mathrm{,}3}{100}}\cdot \frac{1}{1+\frac{10}{100}}=14426}\end{array}$ forint 1994-es vásárlóértékének felelt meg. $c)$ Nagymami ezresre kerekítve 85 000 forintot tett 1994-ben a bankba, számítás az előző módon.   4. Az $ABC$ szabályos háromszög alapú, $D$ csúcsú gúla alapélei $\text{18 cm}$, oldalélei $6\sqrt[]{6}\text{cm}$ hosszúak. Fektessünk az $AD$ éllel párhuzamos síkot az $AB$ és $AC$ élek felezőpontjain át. $a)$ Számítsuk ki a síkmetszet területét. $b)$ Mekkora szöget zár be a metsző sík az alapsíkkal?  (14 pont)   Megoldás. Az $AD$ éllel párhuzamos és az $AB$ és $AC$ élek felezőpontjain átmenő sík az $ABD$ és $ACD$ síkokat az $AD$-vel párhuzamos középvonalakban metszi. A metszetnégyszög paralelogramma, melynek átlói a szimmetria miatt egyenlők, ezért ez téglalap.     $a)$ A téglalap területe $t=9\cdot 3\sqrt[]{6}=27\sqrt[]{6}$. $b)$ A síkmetszet párhuzamos az $AD$ éllel, ezért az alapsíkkal bezárt szögük egyenlő. Mivel $D$ vetülete az $ABC$ szabályos háromszög súlypontja, azért $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{6\sqrt[]{3}}{6\sqrt[]{6}}\mathrm{,}\alpha ={45}^{\circ }\mathrm{.}}\end{array}$   II. rész   5. Egy $16$ fős csoportban a kémia átlag $3\mathrm{,}81$ volt (két tizedesre kerekítve). Tudjuk, hogy senki sem bukott meg. $a)$ Legfeljebb hányan kaphattak kettest? $b)$ Biztos-e, hogy volt valakinek ötöse? $c)$ Hányféleképpen lehetett pontosan $11$ darab négyes? $d)$ Igaz-e, hogy ha a módusz $4$, akkor a medián is $4$?  (16 pont)   Megoldás. Az osztályzatok összegére $\left(x\right)$ teljesül, hogy $3\mathrm{,}805\cdot 16\le x<3\mathrm{,}815\cdot 16$. Egyetlen egész esik a kívánt intervallumba, a 61. $a)$ Legfeljebb hatan, mert hét kettesnél a maradék 9 osztályzat összege 47 kellene legyen, ami lehetetlen. Ha hat kettes, egy négyes és kilenc ötös volt, akkor a feladat minden feltétele teljesül. $b)$ Nem. Lehetett például 3 db hármas és 13 db négyes. $c)$ A 11 négyes mellett nem lehetett a maradék 5 dolgozat mindegyike hármas vagy annál gyengébb, mert az legfeljebb 15 pont a szükséges 17 helyett, ezért biztosan volt ötös. Ha egy darab ötös volt, akkor 4 darab hármas kellett legyen, míg két ötös esetén egy hármas és két kettes osztályzattal jön ki a 17 pont. $d)$ Igaz. Ha a módusz 4, akkor abból legalább öt darab van, különben minden osztályzatból 4 db lenne, de annak az átlaga 3,5. Ha a medián nem 4, akkor a nagyság szerinti nyolcadik‐kilencedik helyen csak hármas és négyes vagy négyes és ötös állhat. Ez utóbbi eset nem lehet, hiszen akkor az utolsó 8 hely mindegyikén ötös áll, de akkor ez a módusz; az első eset pedig azért lehetetlen, mert akkor az utolsó 8 szám összege legfeljebb $5\cdot 4+3\cdot 5=35$, így az első 8 osztályzat összege legalább 26 kellene legyen, ami még $8\cdot 3$-nál is több.   6. Egy derékszögű háromszög beírt körének sugara, körül írt körének sugara és a kerülete egy mértani sorozat három egymást követő tagja. Bizonyítsuk be, hogy ekkor a két hegyesszög tangensének összege $4$.  (16 pont)   Megoldás. Legyen a derékszögű háromszög beírt körének sugara $r$, körül írt körének sugara $R$, befogói $a$ és $b$, átfogója $c$. Mivel külső pontból egy körhöz húzott érintőszakaszok egyenlők, $r=\frac{a+b-c}{2}$, és $R=\frac{c}{2}$ a Thalész-tétel miatt. Felhasználjuk a mértani sorozat tulajdonságát és a Pitagorasz-tételt: $\begin{array}{c}{\displaystyle {\left(\frac{c}{2}\right)}^2=\left(\frac{a+b-c}{2}\right)\left(a+b+c\right)\mathrm{,}{c}^2=a^2+b^2\mathrm{.}}\end{array}$ Rendezve az $a^2-4ab+b^2=0$ egyenlethez jutunk. Osszunk $b^2$-tel. Ekkor $\text{tg}\alpha =\frac{a}{b}$-re másodfokú egyenletet kapunk, amelynek két gyöke $\text{tg}\alpha =2\pm \sqrt[]{3}$. Ez a két szám egymás reciproka, ezért az egyik az egyik hegyesszögnek, másik a másik hegyesszögnek a tangensét adja, és a kettő összege valóban 4.   7. Egy víztorony $\left(P\right)$ távolságát kell az $1:250000$ arányú térkép segítségével az $A$ falutól meghatározni. Ehhez két falu $(B$ és $C)$ $A$-tól való távolságát ismerjük a térképen: $AB=17\mathrm{,}2\text{cm}$, $AC=20\mathrm{,}0\text{cm}$. Lemértük továbbá, hogy $\begin{array}{c}{\displaystyle APB\sphericalangle ={83}^{\circ }\mathrm{,}APC\sphericalangle ={130}^{\circ }\text{és}BAC\sphericalangle ={65}^{\circ }\mathrm{.}}\end{array}$ Mekkora az $AP$ távolság a valóságban?  (16 pont)   Megoldás. Az adatok 3 értékes jegyet tartalmaznak. Jelöljük a $PAB$ szöget $\phi$-vel. Ennek segítségével kifejezhetők az $ABPC$ konkáv négyszög szögei. Felírva két szinusz-tételt az $ABP$ és $ACP$ háromszögekre, majd a két egyenletet egymással elosztva egy trigonometrikus egyenletet kapunk $\phi$-re. Ennek csak a hegyesszögű megoldása értelmes a példában. Ezután $AP$ szakasz kiszámolható. $AP=13\mathrm{,}46$ cm. Figyelembe kell azonban venni a térkép méretarányát, így a valóságban 33,65 km a távolság.       8. Határozzuk meg azt a harmadfokú függvényt, amelyik a következő tulajdonságokkal rendelkezik: $a)$ Belülről érinti az $x^2+y=4$ görbét az $x=0$ pontban. $b)$ A két görbe metszi egymást az $x=2$ pontban. $c)$ A két görbe közé zárt terület a $\left[0;2\right]$ intervallumban $\frac{4}{3}$. Írjuk le a harmadfokú függvény menetét.  (16 pont)   Megoldás. A harmadfokú függvényt keressük $x\mapsto a{x}^3+b{x}^2+cx+d$ alakban: Érinti az $x^2+y=4$ görbét az $x=0$ pontban, ez két dolgot jelent: ‐ Illeszkedik rá a $\left(0;4\right)$ pont, tehát $d=4$ és ‐ A $\left(0;4\right)$ pontban közös a két görbe érintője, tehát a keresett függvény deriváltja a nulla helyen nulla, ahonnan $c=0$. A két görbe metszi egymást az $x=2$ pontban, ezért $8a+4b+4=0$. A két görbe közé zárt terület a $\left[0;2\right]$ intervallumban $\frac{4}{3}$. Mivel a harmadfokú görbe belülről érinti a másodfokút, ezt a területet az alábbi integrál számítja ki: 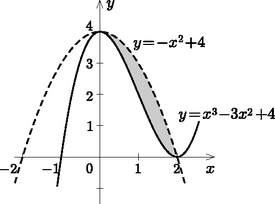$\begin{array}{c}{\displaystyle \underset{0}{\overset{2}{\int }}\left(-x^2+4\right)dx-\underset{0}{\overset{2}{\int }}\left(a{x}^3+b{x}^2+4\right)dx=\frac{4}{3}\mathrm{,}}\end{array}$ ahonnan $3a+2b=-3$.     A keresett függvény tehát $\begin{array}{c}{\displaystyle x\mapsto x^3-3x^2+4=\left(x+1\right){\left(x-2\right)}^2\mathrm{.}}\end{array}$ A függvény menete leolvasható az ábráról.   9. Egy $9$ tagú társaság felszáll a három kocsiból álló HÉV szerelvényre, de a nagy tolongásban a társaság minden tagja csak azt nézi, hogy feljusson valamelyik kocsira, nem törődik azzal, hogy a társai melyik kocsiba szálltak. $a)$ Mennyi a valószínűsége, hogy mindhárom kocsiba a társaság $3$‐$3$ tagja szállt? $b)$ Mennyi a valószínűsége, hogy a három kocsi közül legalább az egyikbe nem szállt fel senki a társaság tagjai közül? $c)$ Mennyi a valószínűsége, hogy a három kocsi közül legalább az egyikbe legfeljebb egy ember szállt fel a társaságból?  (16 pont)   Megoldás. Az, hogy valaki az első, második, harmadik kocsiba szállt, felfogható úgy, hogy kiválasztotta az 1, 2, 3 elemek valamelyikét. Az összes esetek száma ezért $3^9$. $a)$ Annak a valószínűsége, hogy mindhárom kocsiba a társaság 3‐3 tagja szállt, olyan sorozat valószínűségének felel meg, amelyben mindhárom elem 3-szor szerepel: $\begin{array}{c}{\displaystyle p=\frac{\frac{9!}{3{!}^3}}{3^9}\approx 0\mathrm{,}085.}\end{array}$ $b)$ Ez a valószínűség úgy tekinthető, hogy a sorozat minden eleme csak előre meghatározott kettő lehet. Vigyázni kell azonban arra, hogy ne számoljuk többször azokat az eseteket, amikor mindenki ugyanarra a kocsira szállt. $\begin{array}{c}{\displaystyle p=\frac{\left(\genfrac{}{}{0ex}{}{3}{2}\right)2^9-3}{3^9}=0\mathrm{,}07788.}\end{array}$ $c)$ Ha a három kocsi közül legalább az egyikbe legfeljebb egy ember szállt fel, akkor azok a rossz esetek, amikor minden kocsiba legalább ketten szálltak, vagyis ha az emberek eloszlása 2‐2‐5, vagy 2‐3‐4, vagy 3‐3‐3. A keresett valószínűség ezért $\begin{array}{c}{\displaystyle p=1-\frac{3\frac{9!}{2!2!5!}+3!\frac{9!}{2!3!4!}+\frac{9!}{3{!}^3}}{3^9}=0\mathrm{,}4153.}\end{array}$