| Cím: | Érdekességek a glicerin fagyásáról | ||
| Szerző(k): | Radnai Gyula | ||
| Füzet: | 2004/január, 46 - 49. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Egyéb írások | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A glicerin ( Alkalmazzuk a fenti összefüggést először a sok víz, kevés glicerin esetére: Ha bevezetjük a glicerin oldatbeli koncentrációjára, más szóval tömegszázalékára az Most foglalkozzunk azzal az esettel, amikor az elegyben sokkal több a glicerin, mint a víz. Ekkor a fagyáspont csökkenése: Továbbra is a glicerin koncentrációját jelölve Ábrázoljuk mindkét függvényt, s terjesszük ki érvényességüket formálisan egészen addig, amíg a függvényértéket ábrázoló görbék ,,összeérnek'' (1. ábra), majd vessük össze ezt a grafikont reális mérési adatokkal (Beilsteins Handbuch, 1941) (2. ábra). 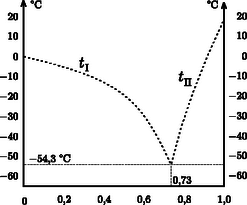 1. ábra 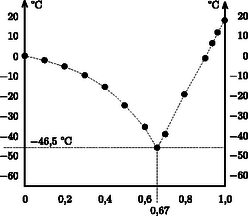 2. ábra Meglepő a hasonlóság! Függvényeink ( Persze a A kétkomponensű elegyek fagyáspont-görbéje általában is ilyen lefutású, mint amit most, a víz‐glicerin elegyre láttunk. Nem véletlenül nevezik ezt fagyáspont-görbének: hűtés közben itt kezdődik meg a fagyás. Jól tudjuk, hogy az egykomponensű, tiszta anyag olvadáspontja megegyezik a fagyáspontjával; akár az olvadás, akár a fagyás ugyanazon a hőmérsékleten történik, s e hőmérséklet állandó marad mindaddig, amíg csak az olvadás vagy a fagyás be nem fejeződik. Jól ismert, hogy a Celsius-skála alappontjait először az olvadó jéghez és a normál légköri nyomáson forrásban levő vízhez kötötték. Az állandó összetételű kétkomponensű elegyet a folyadékállapotból lassan lehűtve akkor érjük el a fagyáspontot, amikor az első kristálydarabkák megjelennek benne. A hűtést tovább folytatva a hőmérséklet azonban már nem marad állandó, hanem csökken. A kifagyott kristályok az oldószerből keletkeznek, ezért a megmaradó folyadékfázis nemcsak egyre hidegebb, de egyre töményebb is lesz. Vizsgáljuk meg a víz + glicerin elegy példáján a kétkomponensű elegyek egyensúlyi fázisdiagramját (3. ábra). 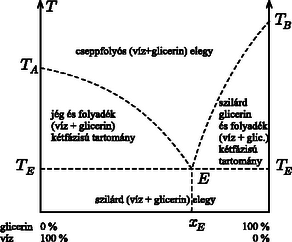 3. ábra Megállapításaink bizonyos fokig a kétkomponensű fémötvözetekre is érvényesek; az ottani szaknyelv eutektikus pontnak nevezi a két fagyáspont-görbe találkozási pontját. Csak az ehhez tartozó Érdekességként megemlítjük, hogy a kétfázisú tartományokban a szilárd fázis mindig csak az egyik komponensből áll, míg a folyadék fázisban a két komponens tömegarányát két szakasz hosszának arányából állapíthatjuk meg. Ha a vizsgált állapotot reprezentáló ponton keresztül húzunk egy vízszintes egyenest az egyensúlyi fázisdiagramon, akkor a ponttól a fagyáspont-görbéig, illetve a függőleges tengelyig tart az egyenesen az említett két szakasz. Ha valaki mégis úgy akarja meghatározni a kétkomponensű elegy fagyáspontját, hogy elég jól lehűti, majd lassan melegíteni kezdi, tisztában kell lennie azzal, hogy legtöbbször a jól lehűtött anyag se fagyott meg egészen. A glicerin híg vizes oldatát megfagyasztva víz-jég keletkezik, amelynek belsejében, felületén még ott a tömény glicerinoldat, csak nem vehető könnyen észre, mert nagyon kicsi a tömege a jég tömegéhez képest. Ha most melegíteni kezdjük, szépen lassan olvad a jég, és nő a hőmérséklet. Az a hőmérséklet lesz a fagyáspont, amikor az utolsó kis jégkristály éppen felolvad. Mielőtt ez az állapot bekövetkezne, a fagyáspontnál alacsonyabb hőmérsékleteken is megfigyelhetünk érdekes tüneményeket, például azt, hogy a jég hókristályszerűvé töredezik, aprózódik szét, ez azonban nem a fázisátalakulás jellegzetes hőmérsékletén történik. Végül érdemes megemlíteni, hogy eddig végig a kétkomponensű rendszerek egyensúlyi állapotairól volt szó. Ha ugyanis túl gyorsan hűtjük vagy fűtjük a rendszert, nem hagyunk időt az egyensúly beállására, úgynevezett ,,nemegyensúlyi'' állapotok alakulhatnak ki. Ezt elsősorban a hőmérséklet inhomogenitása jelzi (más a hőmérséklet az edény szélénél, mint a közepén), s a betett hőmérő által mért értékek reprodukálhatatlansága. Ilyenkor nem a hőmérő hibás, hanem maga az állapot határozatlan. Még egy egykomponensű, tiszta anyagnál is előfordulhat, hogy a folyadékállapotból való gyors lehűtés során az anyag megszilárdul, de nem lesz kristályos szerkezetű. Ezt hívják üvegállapotnak, s üvegesedési hőmérsékletnek azt a hőmérsékletet, amikor az anyag viszkozitása végtelen nagyra nő. Tömény glicerinre ez |
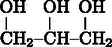 ) az egyik legérdekesebb folyadék. A ,,Négyjegyű'' szerint például a glicerin fagyáspontja C. Sajtóhibára gyanakszunk (talán lemaradt egy negatív előjel), hiszen még senki se látott olyat, hogy megfagyott volna a glicerin a polcon az üvegben, ha csak mondjuk C volt a szobában. Ha utánanézünk komolyabb, részletesebb és pontosabb táblázatokban, nagy meglepetésre azt találjuk, hogy az adat helyes, legfeljebb még egy kissé pontosítható: a glicerin fagyáspontja C.
) az egyik legérdekesebb folyadék. A ,,Négyjegyű'' szerint például a glicerin fagyáspontja C. Sajtóhibára gyanakszunk (talán lemaradt egy negatív előjel), hiszen még senki se látott olyat, hogy megfagyott volna a glicerin a polcon az üvegben, ha csak mondjuk C volt a szobában. Ha utánanézünk komolyabb, részletesebb és pontosabb táblázatokban, nagy meglepetésre azt találjuk, hogy az adat helyes, legfeljebb még egy kissé pontosítható: a glicerin fagyáspontja C.