Kezdőlap


Cím:	A 34. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet:	2003/október, 427 - 432. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 34. Nemzetközi Fizikai Diákolimpia elméleti feladatai¹

1. feladat. Inga, melynek felső végét is egy súly húzhatja

Egy

R

sugarú merev rudat a talaj felett bizonyos magasságban vízszintes helyzetben rögzítettünk. Egy elhanyagolható tömegű,

L

hosszúságú

(L > 2 π R)

fonál egyik végét az 1. ábrán látható módon a rúd legfelső,

A

pontjában rögzítettük, a másik végére

m

tömegű pontszerűnek tekinthető testet erősítve ingát készítettünk. A fonalat feszesen tartva az inga nehezékét az

A

ponttal azonos magasságba emeljük, majd onnan kezdősebesség nélkül elengedjük. A fonalat kezdetben feszültségmentesnek tekinthetjük, és feltehetjük, hogy az ingatest a rúd tengelyére merőleges síkban mozog. A továbbiakban az ingatestet részecskének fogjuk nevezni. A nehézségi gyorsulás

g

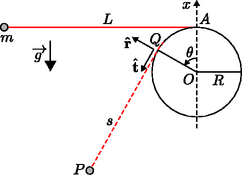1. ábra

Legyen

O

a koordináta-rendszerünk origója! Amikor a részecske a

P

pontban van, a fonál a hengerfelület

Q

pontbeli érintőjével egyirányú. A

Q P

szakasz hosszát

s

-sel jelöljük. A

Q

pontbeli érintő irányú egységvektort jelölje

\hat{t}

, a sugár irányú egységvektort pedig

\hat{r}

. Az

O Q

sugár szögelfordulása

θ

, melyet az

O A

függőleges

x

tengelytől az óramutató járásával ellentétes irányban tekintjük pozitívnak.
Amikor

θ = 0

, az

s

távolság nagysága

L

, és a részecske gravitációs potenciális energiája,

U

legyen nulla. A részecske mozgása során az időben változó

θ

és

s

mennyiségek változási sebességét jelölje

\dot{θ}

és

\dot{s}

. Hacsak nem jelezzük másként, valamennyi sebességet a rögzített

O

pontra vonatkoztatjuk.

A. Ebben a részben a részecske mozgása során a fonál végig feszes marad. A fentebb bevezetett mennyiségek (vagyis

s

θ

\dot{s}

\dot{θ}

R

L

g

\hat{t}

és

\hat{r}

) segítségével fejezzük ki:

a)

\dot{θ}

és

\dot{s}

közötti kapcsolatot (0,5 pont).

b)

A mozgó

Q

pont

O

ponthoz viszonyított sebességvektorát (0,5 pont).

c)

P

pontban levő részecske

Q

ponthoz viszonyított

v_{Q}

sebességvektorát (0,7 pont).

d)

P

pontban levő részecske

v

sebességvektorát az

O

ponthoz viszonyítva (0,7 pont).

e)

P

pontban levő részecske

O

pontra vonatkoztatott gyorsulásának komponensét (0,7 pont).

f)

P

pontban levő részecske

U

gravitációs potenciális energiáját (0,5 pont).

g)

A részecske sebességének

v_{m}

nagyságát a pályájának legalacsonyabb pontjában (0,7 pont).

B. Ebben a részben az

L

és

R

mennyiségek aránya legyen

\begin{matrix} \frac{L}{R} = \frac{9 π}{8} + \frac{2}{3} ctg \frac{π}{16} \approx 6, 886. \end{matrix}

h)

Adjuk meg a részecske sebességének nagyságát (

g

és

R

függvényében) abban a helyzetben, amikor a

Q P

fonalhossz a legrövidebb, de a fonal még nem lazult meg (2,4 pont).

i)

Mekkora a rúd túlsó oldalára átlendült részecske sebessége (

g

és

R

függvényében) a pályájának ottani legmagasabb,

H

pontjában (1,9 pont)?

C. Ebben a részben az

m

tömegű nehezékkel rendelkező inga fonalának felső végét nem rögzítjük az

A

ponthoz, hanem a fonalat a rúd tetején átvetve a végét egy nehezebb,

M

tömegű súlyhoz kapcsoljuk, az 2. ábrán látható módon. A súly ugyancsak pontszerűnek tekinthető. Kezdetben az ingatestet az

A

ponttal azonos magasságban tartjuk, a másik oldalon a súly az

O

pontnál mélyebben helyezkedik el, a fonál feszes, és a vízszintes részének hossza

L

. Ezután az ingatestet kezdősebesség nélkül elengedjük, és a súly is süllyedni kezd. Feltehetjük, hogy az ingatest mindvégig egy függőleges síkban mozog, és át tud lendülni a lefelé mozgó súly mellett, anélkül, hogy egymás mozgását megzavarnák. A rúd felülete és a fonal közötti csúszási súrlódás elhanyagolható, a tapadó súrlódásról viszont feltesszük, hogy az elegendően nagy, és emiatt az egyszer megálló súly nem tud ismét megmozdulni, nyugalomban kell maradjon.

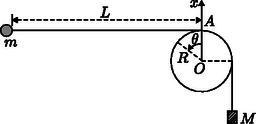2. ábra

j)

Tegyük fel, hogy a súly

D

nagyságú függőleges elmozdulás után valóban megáll, és hogy

(L - D) ≫ R .

Ahhoz, hogy az ingatest a rúd körül teljesen körbefordulhasson, vagyis

θ = 2 π

lehessen, méghozzá úgy, hogy a fonál mindkét ága egyenes maradjon, az szükséges, hogy az

α = D / L

hosszúságarány ne legyen kisebb egy bizonyos kritikus

α_{k}

értéknél.
Elhanyagolva az

R / L

nagyságrendű, vagy ennek magasabb hatványait tartalmazó kicsiny tagokat, adjunk becslést

α_{k}

nagyságára az

M / m

tömegaránnyal kifejezve (3,4 pont)!

2. feladat. Piezoelektromos kristályrezonátor elektromos váltófeszültséggel
Tekintsünk egy homogén,

A

keresztmetszetű rudat, melynek mechanikai feszültségektől mentes állapotban a hossza

ℓ

(3. ábra).

3. ábra

Ha a rúd két végén azonos nagyságú, de ellentétes irányú, a felületre merőleges

F

erő hat, a rúd hossza

Δ ℓ

-lel megváltozik. A

T

mechanikai feszültséget a rúd végein az

F / A

képlet definiálja. A rúd hosszának relatív megváltozását, azaz

Δ ℓ / ℓ

-t deformációnak nevezzük, és

S

-sel jelöljük. A mechanikai feszültség és a deformáció segítségével a Hooke-törvényt a következő alakban is felírhatjuk:

\begin{matrix} T = Y S vagy \frac{F}{A} = Y \frac{Δ ℓ}{ℓ}, \end{matrix}

(1)

ahol

Y

a rúd anyagának Young-modulusa. Jegyezzük meg, hogy

T

nyomó feszültség, ha

F < 0

és a rúd hossza csökken (azaz

Δ ℓ < 0

). Az ilyen feszültség tehát negatív, és értéke a

p

nyomás

(- 1)

-szerese:

T = - p .

Egy homogén,

ϱ

sűrűségű rúdban a longitudinális hullámok terjedési sebessége (azaz a hangsebesség) a következő képlettel adható meg:

\begin{matrix} u = \sqrt[]{\frac{Y}{ϱ}} . \end{matrix}

(2)

(A feladat megoldása során minden csillapítás és elnyelődés elhanyagolható.)

A. Mechanikai tulajdonságok
Egy homogén, egyik irányban végtelen rúd (kiterjedése

x = 0

-tól

\infty

-ig tart), sűrűsége

ϱ

. A rúd kezdetben nyugalomban van és feszültségmentes. A rúd bal felületére az

x = 0

helyen egy nagyon rövid

Δ t

ideig állandó, kicsiny

p

nyomás hat, és ezzel elindít egy

u

sebességgel jobbra haladó nyomáshullámot (4. ábra).

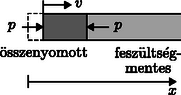4. ábra

a)

Mekkora ez alatt a

Δ t

idő alatt az

S

deformáció és a

p

nyomás a rúd bal oldali felületénél, ha a dugattyú a rúd bal oldali felületét állandó

v

sebességgel mozgatja (4. ábra)? A választ

ϱ

u

és

v

függvényében kell megadni (1,6 pont)!

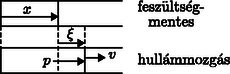5. ábra

b)

Tekintsünk egy longitudinális hullámot, amely

x

irányban terjed a rúdban! Jelöljük a rúd feszültségmentes állapotában

x

helyen levő keresztmetszetének

t

időpontbeli elmozdulását

ξ (x, t)

-vel (5. ábra), és tételezzük fel, hogy

\begin{matrix} ξ (x, t) = ξ_{0} sin k (x - u t), \end{matrix}

(3)

ahol

ξ_{0}

és

k

állandók. Határozd meg a megfelelő

v (x, t)

sebességet,

S (x, t)

deformációt és

p (x, t)

nyomást

x

és

t

függvényében (2,4 pont)!

B. Elektromechanikai tulajdonságok (beleértve a piezoelektromos hatást)
Tekintsünk egy hasáb alakú kvarckristályt, amelynek hossza

b

, vastagsága

h

és szélessége

w

(6. ábra)! A hossza

x

tengely irányú, vastagsága pedig

z

tengely irányú. Az alsó és a felső felületén vékony fémbevonat segítségével elektromos kontaktusokat alakítottak ki. Az elektromos vezetékek, amelyek egyben tartószerkezetként is szolgálnak (7. ábra) a kontaktusok közepére vannak forrasztva, ezért az

x

irányú longitudinális rezgések során ezek a pontok nyugalomban kell maradjanak.

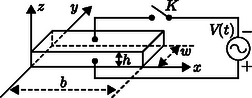6. ábra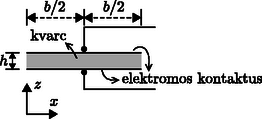

7. ábra

A vizsgált kvarckristály sűrűsége

ϱ = 2, 65 \cdot 10^{3} kg/m^{3}

, Young-modulusa pedig

Y = 7, 87 \cdot 10^{10} N/m^{2}

. A hasáb hossza

b = 1, 00

cm, a

w

szélességre és a

h

vastagságra pedig

h ≪ w ≪ b

teljesül. A

K

kapcsoló nyitva van, és feltételezzük, hogy csak

x

irányú longitudinális módusú állóhullámok gerjesztődnek a kvarc hasábban.
Egy

f = ω / (2 π)

frekvenciájú állóhullámban a

ξ (x, t)

elmozdulás a következő alakba írható:

\begin{matrix} ξ (x, t) = 2 ξ_{0} g (x) cos ω t, (0 \leq x \leq b), \end{matrix}

(4a)

ahol

ξ_{0}

egy pozitív konstans, a

g (x)

helyfüggő tényező

\begin{matrix} g (x) = B_{1} sin k (x - \frac{b}{2}) + B_{2} cos k (x - \frac{b}{2}) \end{matrix}

(4b)

alakú,

g (x)

maximális értéke

1

és

k = ω / u

. Ne felejtsd el, hogy az elektromos kontaktusok közepe nyugalomban van, és hogy a hasáb bal és jobb vége szabad, a mechanikai feszültség (vagy a nyomás) értéke ezeken a helyeken nulla kell legyen!

c)

Határozd meg a

(4 b)

képletben szereplő

B_{1}

és

B_{2}

állandók értékét, ha a kvarc hasábban egy longitudinális állóhullám alakul ki (1,2 pont)!

d)

Mekkora az a két legkisebb frekvencia, amelyen longitudinális állóhullám gerjeszthető a kvarc hasábban (1,2 pont)?

A piezoelektromos hatás a kvarckristály speciális tulajdonsága. A kristály összenyomása vagy megnyújtása elektromos feszültséget hoz létre a kristályban, és fordítva, a kristályra kapcsolt külső elektromos feszültség vagy megnyúlást, vagy összehúzódást okoz, a polaritástól függően. Így a mechanikai és az elektromos rezgések csatolódhatnak és rezonálhatnak a kvarckristályban.
Legyen a felső és az alsó elektromos kontaktus elektromos töltéssűrűsége

- σ

, illetve

+ σ

, ha a kvarc hasábban

E

nagyságú,

z

irányú elektromos tér van! Jelölje a hasáb

x

irányú deformációját és mechanikai feszültségét

S

, illetve

T

! Ekkor a piezoelektromos hatás a kvarckristályban a következő egyenletrendszerrel írható le:

\begin{matrix} S & = (1 / Y) T + d_{p} E, & (5a) \\ σ & = d_{p} T + ε_{T} E, & (5b) \end{matrix}

ahol

1 / Y = 1, 27 \cdot 10^{- 11} m^{2}/N

a Young-modulus reciproka állandó elektromos tér esetén,

ε_{T} = 4, 06 \cdot 10^{- 11} F/m

a dielektromos állandó konstans mechanikai feszültség esetén,

d_{p} = 2, 25 \cdot 10^{- 12}

m/V pedig a piezoelektromos együttható.
Legyen most a 6. ábrán látható

K

kapcsoló zárva! Ekkor

U (t) = U_{m} cos ω t

elektromos váltófeszültség jelenik meg a kontaktusokon, és a kvarc hasábban homogén,

E (t) = U (t) / h

nagyságú,

z

irányú elektromos tér keletkezik. Az állandósult állapot kialakulása után a hasábban egy

x

irányú,

ω

körfrekvenciájú longitudinális állóhullám figyelhető meg.
Mivel

E

homogén, a

λ

hullámhossz és a hasábban lévő állóhullámok

f

frekvenciája között továbbra is érvényes a

λ = u / f

összefüggés, ahol

u

értékét a (2) egyenlet adja meg. A

T = Y S

összefüggés azonban most már nem érvényes, mint ahogy azt az

(5 a)

egyenlet is mutatja. Ugyanakkor a deformáció és a mechanikai feszültség definíciója változatlan, a hasáb végei pedig továbbra is szabadok, nulla mechanikai feszültséggel.

e)

(5 a)

és az

(5 b)

egyenletek figyelembevételével a

σ

felületi töltéssűrűség az alsó elektromos kontaktuson

x

és

t

függvényében

\begin{matrix} σ (x, t) = [D_{1} cos k (x - \frac{b}{2}) + D_{2}] \frac{U (t)}{h} \end{matrix}

alakú lesz, ahol

k = ω / u

. Vezesd le a fenti

D_{1}

és

D_{2}

mennyiségeket megadó összefüggéseket (2,2 pont)!

f)

Az alsó kontaktuson lévő teljes

Q (t)

elektromos töltés az

U (t)

feszültségtől a

\begin{matrix} Q (t) = [1 + α^{2} (\frac{2}{k b} tg \frac{k b}{2} - 1)] C_{0} U (t) . \end{matrix}

képlet szerint függ. Vezesd le a kifejezésben szereplő

C_{0}

és

α^{2}

mennyiségeket megadó összefüggéseket, valamint

α^{2}

numerikus értékét (1,4 pont)!

3. feladat.²
A rész: Neutrínótömeg és neutronbomlás
Egy

m_{n}

nyugalmi tömegű, a laboratóriumi koordináta-rendszerben álló, szabad neutron el tud bomlani három, egymással kölcsönhatásban nem álló részecskére: egy protonra, egy elektronra és egy antineutrínóra. A proton nyugalmi tömege

m_{p}

, az antineutrínó

m_{ν}

nyugalmi tömegéről pedig feltesszük, hogy nem nulla, de sokkal kisebb, mint az elektron

m_{e}

nyugalmi tömege. A vákuumbeli fénysebességet jelölje

c

. A mért értékek a következők:

\begin{matrix} m_{n} = 939, 565 63 MeV/c^{2}, m_{p} = 938, 272 31 MeV/c^{2}, m_{e} = 0, 510 990 7 MeV/c^{2}. \end{matrix}

A továbbiakban minden energia és sebesség a laboratóriumi rendszerben értendő. Legyen a bomlás során keletkező elektron teljes energiája

E

a)

Határozd meg az

E

energia legnagyobb lehetséges

E_{{max}_{}^{}}

értékét és az antineutrínó

v_{m}

sebességét abban az esetben, amikor

E = E_{{max}_{}^{}}

! Mindkét választ a részecskék nyugalmi tömegei és a fénysebesség segítségével kell megadnod. Felhasználva, hogy

m_{ν} < 7, 3 eV/c^{2}

, számítsd ki numerikusan

E_{{max}_{}^{}}

és

v_{m} / c

értékét 3 értékes tizedesjegy pontossággal (4 pont)!

B rész: Lebegtetés fénnyel
Egy

R

sugarú,

m

tömegű átlátszó üveg félgömb törésmutatója

n

. A félgömbön kívül a közeg törésmutatója 1-gyel egyenlő. A félgömb sík lapjának középső részére, a felületre merőlegesen egyenletes eloszlású monokromatikus, párhuzamos lézerfény-nyaláb esik, a 8. ábrán látható módon. A nehézségi gyorsulás

g

, függőlegesen lefelé mutat. A kör keresztmetszetű lézernyaláb

δ

sugara sokkal kisebb, mint

R

. Mind az üveg félgömb, mind pedig a lézernyaláb a

z

tengelyre nézve hengerszimmetrikus.

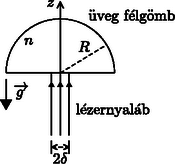8. ábra

Az üveg félgömb semennyit nem nyel el a lézerfényből. A felületét egy átlátszó anyag megfelelő vékonyrétegével vonták be, oly módon, hogy az üvegbe belépő és az onnan kilépő fény visszaverődése elhanyagolhatóan kicsi legyen. A visszaverődésmentes felületi rétegen áthaladó lézerfény optikai úthossza ugyancsak elhanyagolható.

b)

Elhanyagolva a

{(δ / R)}^{3}

és még magasabb hatványú tagokat, határozd meg, hogy mekkora

P

lézerteljesítmény szükséges az üveg félgömb súlyának kiegyensúlyozásához (4 pont)!
Útmutatás:

cos θ \approx 1 - θ^{2} / 2

, ha

θ ≪ 1

¹A részpontszámokat azok kedvéért közöljük, akik ‐ későbbi versenyekre készülve ‐ az olimpiához hasonló feltételek mellett önállóan akarják megoldani a feladatokat. A ,,hivatalos'' megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre.

²Ez a feladat két független részből áll.