Kezdőlap


Cím:	Megjegyzés a B. 3295. feladathoz - alakzatok súlypontjáról
Szerző(k):	Bogdán Zoltán
Füzet:	2000/február, 72 - 75. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások
Hivatkozás(ok):	Feladatok: 1999/szeptember: B.3295

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Gy. 3213. gyakorlatban egy konvex ötszög területét kellett megfelezni kerületének egy kijelölt pontján átmenő egyenessel (megoldása megjelent a KöMaL 1999/3. számában). Az 1999/6. számban kitűzött B. 3295. feladatban az volt a kérdés, hogy a háromszög súlypontján átmenő egyenesek közül melyek felezik a háromszög területét (megoldása e szám 96. oldalán). Aki megoldotta ezeket a feladatokat, rájöhetett: A területfelező nem okvetlenül súlyvonal, a súlyvonal pedig nem mindig területfelező. A második feladatban súlyponton átmenő egyenesekről van szó, amelyek fizikai értelmezés szerint mind súlyvonalak, a matematikai fogalomalkotás szerint viszont a háromszögnek csak három súlyvonala van. A háromszögön túl ‐ pl. egy ötszög esetén ‐ a matematikában alig-alig esik szó súlyvonalról. Az említett két feladat jó alkalom, hogy a súlypontról beszéljünk. Ezt az is indokolja, hogy a dolgozatok javítása közben észrevehetjük: a súlyvonal és a súlypont fogalma a megoldókban kialakulatlan.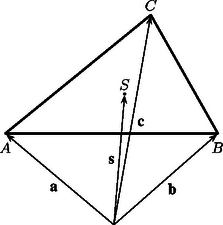
A súlypont fizikai fogalom, amelyet pl. úgy értelmezhetünk, hogy a súlypontban alátámasztott test egyensúlyban van. Másrészt a súlypont fogalmát a matematikában is használjuk (pl. egy háromszög súlypontja vagy egy pontrendszer súlypontja). A közös nevet az indokolja, hogy bizonyos anyageloszlások (homogén háromszöglemez vagy egyenlő tömegű pontszerű testek) esetén a matematikai értelemben vett súlypont megegyezik a fizikaival. Azonban, mint az alábbiakból kiderül, ez nincs mindig így!
1. Pontrendszer súlypontja
a) Egyetlen pont esetén a súlypont azonos a ponttal.
b) Az $A$ , $B$ pontok rendszerének súlypontja az $A B$ szakasznak az az $S$ pontja, amelyre $\vec{S A} + \vec{S B} = 0$ , tehát $S$ az $A B$ felezőpontja.

1. ábra

c) Az

A

B

C

ponthármas súlypontja az az

S

pont, amelyre

\vec{S A} + \vec{S B} + \vec{S C} = 0

, ami az 1. ábra jelöléseivel:

a - s + b - s + c - s = 0

, és így

s = \frac{a + b + c}{3}

.
d) Teljesen hasonlóan kapjuk, hogy az

A_{1}

A_{2}

...

A_{n}

pontrendszer súlypontjának helyvektora

\begin{matrix} s = \frac{a_{1} + a_{2} + ... + a_{n}}{n}, \end{matrix}

(1)

ahol

a_{i}

A_{i}

helyvektora.
2. Súlyozott pontrendszer súlypontja
Ha az 1.d) esetet úgy képzeljük, hogy az

A_{1}

A_{2}

...

A_{n}

pontokban

m_{1}

m_{2}

...

m_{n}

(esetleg nem pozitív) súlyok vannak, akkor a rendszer

S

súlypontjára

\begin{matrix} m_{1} \cdot \vec{S A_{1}} + m_{2} \cdot \vec{S A_{2}} + ... + m_{n} \cdot \vec{S A_{n}} = 0 . \end{matrix}

Ezt a pontok helyvektorával kifejezve:

\begin{matrix} m_{1} (a_{1} - s) + m_{2} (a_{2} - s) + ... + m_{n} (a_{n} - s) = 0, \end{matrix}

amiből

\begin{matrix} s = \frac{m_{1} a_{1} + m_{2} a_{2} + ... + m_{n} a_{n}}{m_{1} + m_{2} + ... + m_{n}}, (m_{1} + m_{2} + ... + m_{n} \neq 0) . \end{matrix}

(2)

(2)-ből látjuk, hogy a közönséges pontrendszert csupa azonos súllyal súlyozott pontrendszernek is tekinthetjük.¹
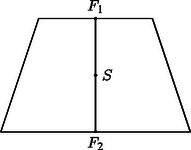
Súlyvonalnak hívunk ezután minden olyan egyenest, amelyik a pontrendszer súlypontján áthalad.
Bizonyítás nélkül megemlítünk két egyszerű tételt:
1. tétel. Ha egy súlyozott pontrendszert két, közös pont nélküli halmazra bontunk, és az egyiknek a súlypontja

S_{1}

, a benne lévő pontok súlyainak összege

M_{1}

, ugyanezek az adatok a másik halmaznál

S_{2}

és

M_{2}

, akkor a pontrendszer

S

súlypontja az

S_{1} S_{2}

egyenesen van, és

S_{1} S : S S_{2} = M_{2} : M_{1}

(

S_{1} S

és

S S_{2}

irányított szakaszok).
2. tétel. Ha egy súlyozott pontrendszer súlyai nem negatívak, akkor a súlypont benne van a pontrendszer konvex burkában.
Mindkét tétel (2)-ből levezethető.
Az alábbiakban nemcsak véges pontrendszerek súlypontját vizsgáljuk. Ehhez az 1. tétel értelemszerű kiterjesztésére van szükség, pontosabban arra, hogy ha egy ponthalmazt két részhalmazra osztunk, akkor a részhalmazok súlypontján átmenő egyenes súlyvonal, tehát átmegy a súlyponton.
3. A háromszög súlypontja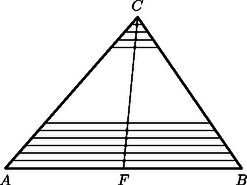

a) A három pontból álló pontrendszer súlypontjának helyvektora̲

\begin{matrix} s = \frac{a + b + c}{3} . \end{matrix}

2. ábra

b) Homogén anyageloszlású háromszöglemez súlypontja̲

Ha egy lemeznek nincsen legalább két szimmetriatengelye, a súlypont matematikai meghatározása általában nehéz feladat, integrálszámítással törtéhet. A 2. ábrán ‐ az integrálszámítást megkerülve ‐ azt láthatjuk, hogyan határozta meg Arkhimédész a háromszöglemez súlypontját. Ő úgy okoskodott, hogy ha a háromszöget az

A B

oldalával párhuzamos keskeny sávokra bontja, akkor mindegyik sáv súlypontja ‐ a szimmetria miatt ‐ rajta lesz a

C F

egyenesen (

F

A B

szakasz felezőpontja), ezért

C F

egy súlyvonal. Ugyanígy kaphatunk egy másik súlyvonalat, és a két súlyvonal metszéspontja a súlypont. Tehát a háromszöglemez súlypontja ugyanaz lesz, mint a három csúcsból álló pontrendszeré.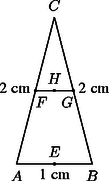

c) Vékony, állandó keresztmetszetű és homogén drótból készült egyenlő szárú há-̲

romszög alakú keret súlypontja̲

3. ábra

A 3. ábrán 1 cm hosszú drót tömege legyen 1 g. Az

A C B

,,törött'' drótszakaszt

A C

és

C B

darabokból összetéve a súlypont az egyenlő tömegű

A C

, illetve

B C

részek

F

G

súlypontját (felezőpontját) összekötő szakasz

H

felezőpontja és összesen 4 g tömeget képvisel. Az

A B

szakasz 1 g tömege pedig a drótszakasz

E

súlypontjába (felezőpontjába) vonható össze. A keret súlypontja ezután a

H E

szakasz

H

-hoz közelebbi ötödölő pontja. Itt felhasználtuk azt a tényt, hogy egy testet két részre vágva, de a részeket helyben hagyva, a részek súlypontjait összekötő egyenes a test egy súlyvonala. Felhasználtuk továbbá, hogy (2)-ből az

n = 2

esetben az következik, hogy két pontszerű tömeg súlypontja a pontok összekötő szakaszát a tömegekkel fordított arányban osztja.

4. A négyszög súlypontja

a) Húrtrapézt alkotó pontnégyes súlypontja̲

A 4. ábrán

F_{1}

, illetve

F_{2}

az alapok felezőpontjai. Az

S

súlypont az

F_{1} F_{2}

szakasz felezőpontja.

4. ábra

5. ábra

b) Húrtrapéz alakú homogén lemez súlypontja̲

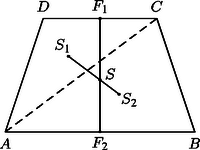
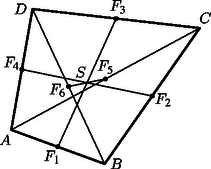
Az 5. ábrán

F_{1} F_{2}

szimmetriatengely, tehát súlyvonal. Az

A C D

háromszög

S_{1}

és az

A B C

háromszög

S_{2}

súlypontját összekötve egy másik súlyvonalat kapunk. A két súlyvonal

S

metszéspontja a súlypont.
Az a) és b) eset azt mutatja, hogy négyszögek esetén a négy csúcs pontrendszerének súlypontja különbözhet a négyszöglemez súlypontjától.

c) Tetszőleges pontnégyes súlypontja̲

Ha az

F_{i}

pontok (

i = 1

, 2,

...

, 6) a 6. ábrán látható megfelelő szakaszok felezőpontjai, akkor például

F_{1} F_{3}

felezőpontjaként kaphatjuk az

S

súlypontot. Ha a csúcsokba mutató vektorokat a megfelelő kisbetűvel jelöljük, akkor

S

-nek az

s

helyvektora.

\begin{matrix} s = \frac{\frac{a + b}{2} + \frac{c + d}{2}}{2} = \frac{\frac{a + d}{2} + \frac{b + c}{2}}{2} = \frac{\frac{a + c}{2} + \frac{b + d}{2}}{2} . \end{matrix}

(3)

Ha a négy pont nincs egy síkban, akkor egy tetraédert határoz meg. (3)-ból következik, hogy a tetraéder szemközti éleinek felezőpontját összekötő szakaszok egy ponton mennek át, ez a pont a pontrendszer súlypontja, és felezi a szóbanforgó szakaszokat.
Bebizonyítható, hogy a homogén anyageloszlású tetraéder alakú test súlypontja megkapható az előbbi módon (6. ábra).

6. ábra

7. ábra

d) Homogén anyageloszlású (sík)négyszöglemez súlypontja̲

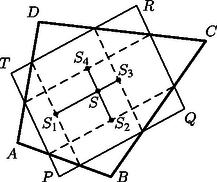
A 7. ábrán az

A B C D

minden oldalát három egyenlő részre osztottuk. Az osztópontokat az ábra szerint összekötve a

P Q R T

paralelogrammát, az úgynevezett Wittenbauer-paralelogrammát kapjuk.

S_{1}

A B D

háromszög,

S_{3}

pedig a

B C D

háromszög súlypontja, ezért

S_{1} S_{3}

a négyszög egy súlyvonala. Hasonlóan súlyvonal

S_{2} S_{4}

is, ezért

S

a négyszög súlypontja. Mivel

S_{1} S_{3}

, illetve

S_{2} S_{4}

illeszkednek a Wittenbauer-paralelogramma középvonalaira,

S

ennek a paralelogrammának a középpontja.
5. Az elmondottak alapján tetszőleges (súlyozott) pontrendszer, vagy homogén sokszöglemez súlypontja megszerkeszthető. A tetraéderrel kapcsolatos tétel alapján bizonyos testek súlypontja is meghatározható.

Bogdán Zoltán

¹Bár pontrendszer súlypontját annak helyvektorával adtuk meg, könnyen ellenőrizhető, hogy maga a súlypont nem függ az origó megválasztásától. (A szerk.)