Kezdőlap


Cím:	Mikor kommutatív, illetve asszociatív a hatványozás?
Szerző(k):	Lóczi Lajos
Füzet:	2000/január, 7 - 16. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az összeadás és a szorzás jól ismert tulajdonságai a kommutativitás és az asszociativitás: ha $a$ és $b$ tetszőleges valós számok, akkor

\begin{matrix} a + b = b + a és a \cdot b = b \cdot a, \end{matrix}

illetve

\begin{matrix} (a + b) + c = a + (b + c) és (a \cdot b) \cdot c = a \cdot (b \cdot c) . \end{matrix}

Tudjuk azonban, hogy a hatványozás már nem rendelkezik ezzel a két tulajdonsággal; tetszőleges

(a, b)

számpárra (illetve

(a, b, c)

számhármasra) általában

\begin{matrix} a^{b} \neq b^{a} és {(a^{b})}^{c} \neq a^{(b^{c})} . \end{matrix}

Ám ez még nem zárja ki azt, hogy bizonyos esetekben egyenlőség álljon fenn. Cikkünkben megkeressük az összes olyan (pozitív) valós számpárt és számhármast, amelyekre a hatványozás kommutatív, illetve asszociatív, segítségükkel pedig az egész és a racionális számok körében is megvizsgáljuk a kérdést.

A kommutatív eset

Jelölésünket némileg módosítva keressük tehát az

x^{y} = y^{x}

egyenletet kielégítő

x

és

y

pozitív valós számokat. (Azért szorítkozunk a továbbiakban csak pozitív számokra, mert negatív alap esetén a hatványozás nincs minden kitevőre definiálva a valós számkörben, valamint az az eset sem különösebben érdekes, ha

x

vagy

y

valamelyike 0-val egyenlő.) Az elinduláshoz ‐ mint új problémák esetén oly gyakran ‐ először próbáljunk egy-két megoldást megsejteni. Viszonylag hamar rátalálhatunk az

x = 2

y = 4

számpárra (természetesen az egyenlet szimmetriája miatt a fordított szereposztás is megfelelő). Mivel több egész megoldás nem látszik, próbálkozzunk gyökös kifejezésekkel. Ha szerencsénk van, rájöhetünk, hogy

x = \sqrt[]{3}

és

y = 3 \sqrt[]{3}

megfelelő, ugyanis

\begin{matrix} {(3 \sqrt[]{3})}^{\sqrt[]{3}} = {({\sqrt[]{3}}^{3})}^{\sqrt[]{3}} = {\sqrt[]{3}}^{(3 \sqrt[]{3})} . \end{matrix}

Itt a hatványozás jól ismert tulajdonságán kívül azon múlott a dolog, hogy

3 \sqrt[]{3}

felírható, mint

{\sqrt[]{3}}^{3}

. Némi további gondolkodás után rátalálunk az

x = \sqrt[3]{4}

y = 4 \sqrt[3]{4}

párra; ez is jó, hiszen

\begin{matrix} {(4 \sqrt[3]{4})}^{\sqrt[3]{4}} = {({\sqrt[3]{4}}^{4})}^{\sqrt[3]{4}} = {\sqrt[3]{4}}^{(4 \sqrt[3]{4})} . \end{matrix}

A lényeg itt is az, hogy

4 \sqrt[3]{4} = {\sqrt[3]{4}}^{4}

. Mindkét (sőt, mindhárom) példában megfigyelhetjük, hogy

y = v x

alakú, ahol

v x = x^{v}

. Próbáljunk meg ezen a nyomon elindulni.

Új változó bevezetése

A fenti észrevétel szerint keressük

y

-t

y = v x

alakban, ahol

v

valós paraméter. (Úgy is fogalmazhatunk, hogy bevezetjük a

v = \frac{y}{x}

új változót. Nyilván

v > 0

.) Ekkor az egyenlet így írható át:

\begin{matrix} {(v x)}^{x} = y^{x} = x^{y} = x^{v x} = {(x^{v})}^{x} . \end{matrix}

Mivel itt minden érték pozitív, a két szélső kifejezést

\frac{1}{x}

-edik hatványra emelve adódik, hogy

v x = x^{v}

, tényleg ezen múlik a megoldás. Most

\frac{1}{x}

-szel szorozva kapjuk, hogy

v = x^{v - 1}

. Ha

v \neq 1

‐ azaz

x \neq y

‐, akkor

\frac{1}{v - 1}

-edik hatványra emelve

x = v^{\frac{1}{v - 1}}

-et nyerjük.

y

-ra pedig ezt kapjuk:

\begin{matrix} y = v x = v \cdot v^{\frac{1}{v - 1}} = v^{\frac{1}{v - 1} + 1} = v^{\frac{v}{v - 1}} = x^{v} . \end{matrix}

Ha viszont

v = 1

, akkor

y = x

adódik, ami nyilván megoldás.
A továbbiakban gyakran szerepel a fenti,

x

-re kapott kifejezés, vezessük erre be a

h (v)

jelölést: legyen

h (v) = v^{\frac{1}{v - 1}}

. A

h (v)

függvény értelmezési tartománya az 1-től különböző pozitív valós számok halmaza, értéke nyilván mindig pozitív.
Megkaptuk a lehetséges megoldásokat, hátravan még annak ellenőrzése, hogy ezek tényleg megoldások-e. A

v = 1

esetben, ha

x

tetszőleges pozitív valós szám, akkor

y = x

nyilván megoldás; nevezzük ezeket triviális megoldásoknak. Ha

v \neq 1

, akkor

x = h (v)

és

y = v \cdot h (v)

szintén megoldások (hívjuk őket nemtriviális megoldásoknak), hiszen mint láttuk,

y = v x = x^{v}

, és így

\begin{matrix} y^{x} = {(x^{v})}^{x} = x^{v x} = x^{y} . \end{matrix}

Első célunkat elértük, előállítottuk az

x^{y} = y^{x}

egyenlőségnek eleget tevő

(x, y)

pozitív valós számpárokat:

(x, x)

, illetve

(h (v), v \cdot h (v))

alakban (

v > 0

v \neq 1

).
A talált

h (v)

függvény érdekes tulajdonságokkal rendelkezik. Ha

v > 0

v \neq 1

továbbra is, akkor

h (v)

az az érték, amelynél mindegy, hogy megszorozzuk-e

v

-vel, avagy a

v

-edik hatványra emeljük, eredményül ugyanazt kapjuk:

v \cdot h (v) = h {(v)}^{v}

, ahogy azt az imént láttuk. Egy másik függvényegyenlet, amelynek

h

eleget tesz, a következő:

v \cdot h (v) = h (\frac{1}{v})

, illetve az osztással adódó

h (v) = \frac{1}{v} \cdot h (\frac{1}{v})

alak. (Gyakorlásként ellenőrizzük helyességüket.)
Ebből az is látszik, hogy a nemtriviális megoldások

(h (v), h (\frac{1}{v}))

alakba is írhatók, tehát az

(x, y)

párból a

v \to \frac{1}{v}

helyettesítéssel az

(y, x)

megoldást kapjuk.
A

h

függvény nem értelmes, ha

v = 1

, ugyanakkor megmutatható, hogy szigorúan monoton fogyó, és

{lim}_{}^{}_{v \to 1}^{} h (v) = e

(a természes alapú logaritmus alapszáma,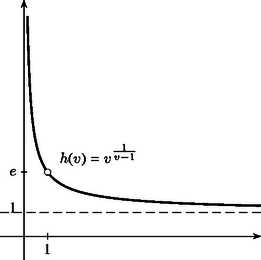

e = 2,71828 ...

)

1. ábra

Egy kis analízis

Szeretnénk az

x^{y} = y^{x}

egyenlet fent nyert megoldásait grafikusan ábrázolni. A triviális megoldás az

x

;

y

koordinátasíkon az 1. negyed szögfelező egyenese (vagyis az

y = x

egyenletű félegyenes,

x

y > 0

esetén). A nemtriviális megoldás viszont nem a szokásos

y = f (x)

alakban áll előttünk:

y

-t nem

x

függvényeként sikerült megkapnunk, hanem

x

is és

y

is a

v

paraméter függvénye. A talált jellemzésből ugyanakkor látszik, hogy a

h

értékkészletébe tartozó tetszőleges

x

-hez egy és csak egy tőle különböző

y

tartozik, amelyre

x^{y} = y^{x}

, így az

f : x \to y

függvény mindenesetre létezik. Elvben nem is lenne akadálya, hogy a nemtriviális megoldásokat ilyen

(x, f (x))

alakba írjuk. Jelölje ugyanis

h^{[- 1]}

a fent definiált

h

függvény inverz függvényét (

h

szigorú monotonitása miatt ez létezik), ekkor

x = h (v)

-ből

v = h^{[- 1]} (x)

, így

(h (v), v \cdot h (v)) = (x, h^{[- 1]} (x) \cdot x)

a keresett alakú (az

f (x) = x \cdot h^{[- 1]} (x)

választással). Ez az átalakítás azonban nem ad lényeges információt a továbblépéshez, mert az

x = h (v)

egyenletből

v

kifejezése, vagyis a

h^{[- 1]}

függvény meghatározása elemi módon (,,képlettel'') ‐ úgy tűnik ‐ nem lehetséges.
Így a paraméteres előállításban szereplő két függvény,

h (v)

és

v \cdot h (v)

viselkedését vizsgáljuk tovább; ennek eredményeként az általuk (mint koordinátafüggvények által) leírt görbét ‐ a nemtriviális megoldásokat ‐ fel fogjuk tudni vázolni. Ezt a görbét a triviális megoldással egy koordináta-rendszerben ábrázolva kapunk teljes képet az egyenlet pozitív valós megoldásairól.
A vizsgálathoz szükség van a határérték és a derivált fogalmára (néhány nevezetes határértékkel együtt); részben emiatt, részben pedig terjedelmi okokból ezeket a bizonyításokat nem közöljük.
Bizonyos mértékben egyszerűsíti a továbbiakat (és egyéb összefüggésekre mutat rá), ha ismét új változót vezetünk be, ,,átparaméterezzük'' függvényeinket. Jelölje

u

h (v)

függvényben

v

kitevőjét, azaz

u = \frac{1}{v - 1}

. Ebből

v = 1 + \frac{1}{u}

adódik. Függvényeink ezzel az új változóval a

\begin{matrix} h (v) = {(1 + \frac{1}{u})}^{u}, illetve a v \cdot h (v) = {(1 + \frac{1}{u})}^{u + 1} \end{matrix}

alakot öltik. Jelöljük az

u

változó ezen új függvényeit rendre

g_{1} (u)

, illetve

g_{2} (u)

-val. Nem nehéz látni, hogy a

g_{1}

függvény grafikonja és a

g_{2}

függvény grafikonja egymás tengelyes tükörképei. A tengely az

x = - \frac{1}{2}

egyenes: a számegyenesen ugyanis egy

u

pont

(- \frac{1}{2})

-re vonatkozó tükörképe

(- u - 1)

, és

u

helyett

(- u - 1)

-et helyettesítve

g_{1}

-ben a függvény éppen

g_{2}

-be megy át. Formálisan:

g_{1} (- u - 1) = g_{2} (u)

, és fordítva,

g_{2} (- u - 1) = g_{1} (u)

.
Elég tehát a továbbiakban pl. a

g_{1}

függvénnyel foglalkozni, ebből

g_{2}

tulajdonságai egyszerűen leolvashatók. Mivel

v

az 1-től különböző pozitív számokat futja be, könnyen ellenőrizhető, hogy a helyettesítés után

u

R ∖ [- 1, 0]

halmazon fog végigfutni (itt a szögletes zárójel a zárt intervallumot jelöli,

R

a valós számok halmaza). Ez tehát

g_{1}

értelmezési tartománya. A

g_{1}

függvény viselkedéséről a következő ismert határértékek nyújtanak felvilágosítást (értelmezési tartományának határpontjaiban vizsgálva):

{lim}_{}^{}_{u \to \infty}^{} g_{1} (u) = e

, alulról tartva.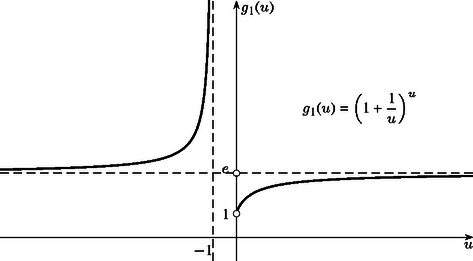

2. ábra

{lim}_{}^{}_{u \to 0 + 0}^{} g_{1} (u) = 1

, felülről, ugyanis ez a (jobb oldali) határérték a

w = \frac{1}{u}

helyettesítéssel visszavezethető

{lim}_{}^{}_{w \to \infty}^{} \sqrt[w]{w + 1} = 1

-re.

{lim}_{}^{}_{u \to - 1 - 0}^{} g_{1} (u) = + \infty

, hiszen az alap felülről 0-hoz tart, míg a kitevő

(- 1)

-hez.

{lim}_{}^{}_{u \to - \infty}^{} g_{1} (u) = e

, felülről tartva, a

w = - u

helyettesítéssel látható be.
A

g_{1}

függvény folytonos az értelmezési tartományán. Megmutatható, hogy szigorúan monoton növő a

(- \infty; - 1)

és a

(0; + \infty)

intervallumokon. A

g_{1}

függvény grafikonját lásd a 2. ábrán.
Minden lényeges információ a rendelkezésünkre áll a

g_{1}

függvényről (és ezzel együtt ,,párjáról'',

g_{2}

-ről is). Mindezeket figyelembe véve, ábrázolhatjuk az

x^{y} = y^{x}

egyenlet nemtriviális megoldásait a

(g_{1} (u), g_{2} (u))

paraméteres alakból, ahol

u \in R ∖ [- 1, 0]

. (Természetesen ez ekvivalens az eredeti

(h (v), v \cdot h (v))

v > 0

v \neq 1

paraméterezéssel (3. ábra).) Amint

u

(- \infty)

-től

(- 1)

-ig nő, a

(g_{1} (u), g_{2} (u))

pontok a 3. ábrán a jobb alsó görbedarabot írják le, mert az első koordinátafüggvény

e

-től

\infty

-ig nő, míg a második koordinátafüggvény

e

-től 1-ig csökken, szigorúan monoton módon. Amint pedig

u

0-tól

+ \infty

-ig nő, a

(g_{1} (u), g_{2} (u))

pontok a bal felső görbedarabot fogják kirajzolni, ugyanis az első koordináta 1-től

e

-ig növekszik, a második koordináta

+ \infty

-ről

e

-re csökken, szintén szigorúan monoton módon. A

45^{\circ}

-os egyenes, ahogyan e rész elején láttuk, a triviális megoldásból származott. A 3. ábrán látható az összes pozitív

(x, y)

számpár, amelyekre a hatványozás kommutatív. A megoldások szimmetriája azt jelenti, hogy a görbe szimmetrikus az

y = x

egyenesre. A triviális és a nemtriviális megoldások görbéi az

(e, e)

pontban találkoznak.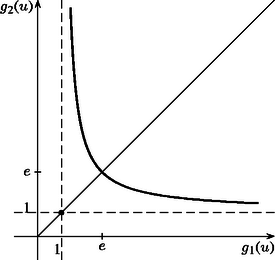

3. ábra

Néhány egyszerű következmény

A fentiek alapján megállapíthatjuk például, hogy a hatványozás nem lehet kommutatív, ha az alap és a kitevő mindketten 1-nél kisebb, különböző számok, hiszen a nemtriviális esetben a

g_{1}

és

g_{2}

függvények értékei nagyobbak 1-nél. Hasonlóan látható a grafikonról, hogy ha

x

y > e

és

x \neq y

, akkor

x^{y}

szintén nem egyenlő

y^{x}

-nel.
Ha az

x^{y}

kifejezésben

x

és

y

helyére beírjuk a paraméteres előállítást, akkor a

\begin{matrix} h {(v)}^{[v \cdot h (v)]} = v^{v^{\frac{v}{v - 1}} / (v - 1)} \end{matrix}

kifejezést kapjuk. Erről a függvényről belátható, hogy értékkészlete az

(e^{e}, \infty)

intervallum. Ebből következik például, hogy ha egy

x^{y}

hatvány értéke kisebb

e^{e}

-nél és

x \neq y

, akkor

x^{y} \neq y^{x}

Az egész és racionális megoldások

A pozitív valós megoldások után térjünk most rá az

x^{y} = y^{x}

egyenlet pozitív egész, illetve pozitív racionális megoldásainak megkeresésére. A triviális eset egyszerű: bármely

x

egész, illetve racionális szám megfelelő (

y = x

x > 0

). A nemtriviális eset összetettebb. Az egész megoldásokat a grafikonról is leolvashatjuk: a bal felső ág első koordinátájára

1 < x < e

, és

e < 3

miatt ilyen egész csak

x = 2

lehet, ehhez pedig az

y = 4

érték tartozik. Így a bal felső ág az egész rácspontok közül csak az

(x, y) = (2, 4)

-en halad át. A szimmetria miatt a jobb alsó ág egyetlen rácspontja az

(x, y) = (4, 2)

pont. Az összes egész megoldást megtaláltuk.
Vizsgáljuk most a racionális megoldásokat. A

v

paraméter olyan értékeit keressük, amelyekre a

(h (v), v \cdot h (v))

pár mindkét tagja pozitív racionális szám. Ha

h (v)

racionális, akkor

v \cdot h (v)

csak úgy lehet racionális, ha

v

maga is racionális, mert

h (v)

mindig pozitív.

v

-t így elég a

\frac{p}{q}

alakú számok közt keresnünk, ahol

p

q

pozitív egészek, és föltehető, hogy relatív prímek. Figyelembe véve, hogy nemtriviális megoldást keresünk,

v \neq 1

kell legyen, ezért

p \neq q

. Láttuk, hogy ha

v

helyett

\frac{1}{v}

-t írunk a paraméterezésben, mindössze annyi történik, hogy

x

és

y

felcserélődnek. Ezért elég a

v > 1

esettel foglalkozni, elég tehát

p > q

-t nézni. (Azaz csak a 3. ábra bal felső ágán vizsgálódunk.) Az egész megoldásokat már megkaptuk,

q = 1

-gyel sem kell törődnünk. Emiatt

p > q > 1

is feltehető. Beírva

v

helyére

\frac{p}{q}

-t, kapjuk, hogy

\begin{matrix} h (v) = {(\frac{p}{q})}^{\frac{q}{p - q}} . \end{matrix}

Legyen

m = p - q

, ekkor

m \geq 1

egész. Megmutatjuk, hogy ha

m > 1

, akkor

h (\frac{p}{q}) = \sqrt[m]{\frac{p^{q}}{q^{q}}}

nem lehet racionális. Most

(p, q) = 1

, ezért a

\frac{p^{q}}{q^{q}}

tört sem egyszerűsíthető. Egy ilyen tört

m

-edik gyöke viszont csak úgy lehet racionális, ha a számlálója és a nevezője is teljes

m

-edik hatvány.
Legyen ugyanis

\sqrt[m]{\frac{r}{s}} = \frac{a}{b}

, ahol

(r, s) = 1

(a, b) = 1

föltehető és

r

s

a

b > 0

. Ekkor

\frac{r}{s} = \frac{a^{m}}{b^{m}}

, másrészt

(a, b) = 1

-ből

(a^{m}, b^{m}) = 1

következik. Mivel egy racionális szám egyszerűsített alakja egyértelmű (a számláló és a nevező pozitív), mind

r

, mind pedig

s

teljes

m

-edik hatvány.
Így ha most

h (\frac{p}{q})

racionális, akkor

p^{q} = a^{m}

és

q^{q} = b^{m}

. Megmutatjuk, hogy ha

q

és

m

relatív prímek ‐ ami most teljesül, hiszen

p = q + m

és

(p, q) = 1

‐, akkor

p

is és

q

is teljes

m

-edik hatványok.
Valóban, ha egy tetszőleges prímszám kitevője a

p

prímtényezős felbontásában

k

, akkor

p^{q}

-ban

k \cdot q

, ami most osztható

m

-mel. Innen pedig

(m, q) = 1

miatt

m ∣ k

következik, a

p

tehát valóban teljes

m

-edik hatvány. Ugyanígy kapjuk, hogy a

q

is teljes

m

-edik hatvány.
Az

m = p - q

egyenlőség ezután már nem lehetséges, hiszen két különböző

m

-edik hatvány különbsége nagyobb, mint

m

. Ha ugyanis

t_{1} > t_{2} > 0

egészek, akkor

\begin{matrix} t_{1}^{m} - t_{2}^{m} = (t_{1} - t_{2}) (t_{1}^{m - 1} + t_{1}^{m - 2} t_{2} + ... + t_{1} t_{2}^{m - 2} + t_{2}^{m - 1}), \end{matrix}

és a jobb oldal határozottan nagyobb, mint

(t_{1} - t_{2}) \cdot m \cdot t_{2}^{m - 1}

, ami legalább

m

.
Ezzel igazoltuk, hogy ha

m = p - q > 1

, akkor

h (\frac{p}{q})

irracionális.
Maradt az

m = 1

, azaz a

p = q + 1

eset. Ekkor

h (v) = {(\frac{q + 1}{q})}^{q}

, nyilván racionális,

v \cdot h (v)

-re pedig

{(\frac{q + 1}{q})}^{q + 1}

adódik.

q

helyett a szokásosabb

n

változóval felírva megkaptuk a pozitív racionális megoldásokat

\begin{matrix} x = {(1 + \frac{1}{n})}^{n}, illetve y = {(1 + \frac{1}{n})}^{n + 1}, \end{matrix}

ahol

n > 1

egész. (Ha

n = 1

, akkor az

x = 2

y = 4

megoldást kapjuk meg újra.) Természetesen

x

és

y

most is felcserélhetők. Ezek tehát a 3. ábra nemtriviális görbéjének azon pontjai, amelyeknek mindkét koordinátája racionális.
Az analízisben az

{(1 + \frac{1}{n})}^{n}

, illetve az

{(1 + \frac{1}{n})}^{n + 1}

számokból képezett sorozatok azért nevezetesek, mert mindkettőjük határértéke (

n \to \infty

esetén) az

e

szám. Általában éppen így definiálják az

e

számot. Mi most egy másik különleges tulajdonságukat találtuk: a hatványozás a (különböző, pozitív) racionális számok körében csak ezen számok esetén kommutatív.

Egy másik megközelítés

A kommutatív eset lezárásaként megemlítünk egy másik utat, amelyen az

x^{y} = y^{x}

egyenlet vizsgálatakor elindulhatnánk. Tulajdonképpen az egyenlet (ekvivalens módon történő) átfogalmazásáról van szó: ha mindkét oldalt

\frac{1}{x \cdot y}

-adik hatványra emeljük
(

x

y > 0

), akkor az

x^{\frac{1}{x}} = y^{\frac{1}{y}}

alakhoz jutunk. Az eredetihez képest itt a két oldalon ugyanannak a függvénynek két (nem feltétlenül különböző helyen vett) helyettesítési értékéről van szó: az

f (t) = t^{\frac{1}{t}}

(

t > 0

valós szám) jelölés bevezetésével az egyenlet az

f (x) = f (y)

(eredetivel ekvivalens) alakot ölti.
Nyilván megoldást kapunk, ha

x = y

. A kérdés az, hogy

x \neq y

esetén állhat-e egyenlőség. Némi elemzéssel (határérték, monotonitás) az

f

függvényről megállapítható, hogy a

(0, 1]

jobbról zárt intervallumot önmagára képezi (kölcsönösen egyértelműen), míg az

(1, e)

, illetve

(e, \infty)

nyílt intervallumokat mind az

(1, e^{\frac{1}{e}})

intervallumra képezi. (Az

(1, e)

intervallumon szigorúan monoton nő,

(e, \infty)

-en szigorúan monoton csökken.) Ezekből következik (a függvény folytonosságát használva), hogy az eredeti egyenletnek van nemtriviális megoldása:

1 < x < e

esetén van olyan

y

, amelyre

f (x) = f (y)

(ekkor a fentiekből

e < y < \infty

adódik, és

y

egyértelmű). Persze fordítva is igaz: minden

e < x < \infty

számhoz létezik egyetlen olyan

y

szám (

1 < y < e

), amelyre

f (x) = f (y)

(4. ábra). Az

x \in (0, 1]

, illetve

x = e

számok esetén csak

y = x

mellett lehet

f (x) = f (y)

.
Összefoglalva, az

x \in (0, 1]

vagy

x = e

számokhoz egyetlen

y

, míg az

x \in (1, e)

vagy

x \in (e, \infty)

számokhoz két olyan

y

létezik, amelyekre

x^{y} = y^{x}

. Ebben a megközelítésben, ha nem is maguk a megoldások, de legalább a megoldások száma könnyen kideríthető.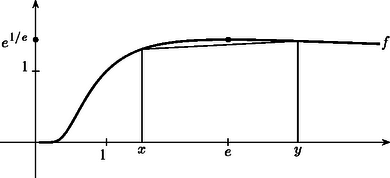

4. ábra

Az asszociatív eset

Feladatunk most az összes olyan pozitív valós

(x, y, z)

számhármas megkeresése, amelyre

\begin{matrix} {(x^{y})}^{z} = x^{(y^{z})} . \end{matrix}

A bal oldal nyilván

x^{y z}

alakban is felírható. Ha

x \neq 1

, akkor

y z = y^{z}

adódik. Éppen ezzel a feltétellel talákoztunk a kommutatív eset vizsgálatakor. Ha

z = 1

, akkor minden pozitív

y

megoldás, egyébként

y = h (z)

.
Megkaptuk az összes pozitív valós számhármast, amelyekre a hatványozás asszociatív (lásd az 5. ábrát):

\begin{matrix} \begin{matrix} (1, y, z), & ahol & y, z > 0, \\ (x, y, 1), & ahol & x \neq 1, x, y > 0, \\ (x, h (z), z), & ahol & x \neq 1, z \neq 1; x, z > 0. \end{matrix} \end{matrix}

Az egész és racionális megoldások

A racionális megoldásokat ‐ a kommutatív esetben elvégzett vizsgálatoknak köszönhetően ‐ könnyen felírhatjuk. A valós megoldásokból kiindulva látható, hogy a pozitív, racionális számok körében a hatványozás akkor asszociatív, ha az

(x, y, z)

hármas az alábbiak valamelyikével egyezik meg: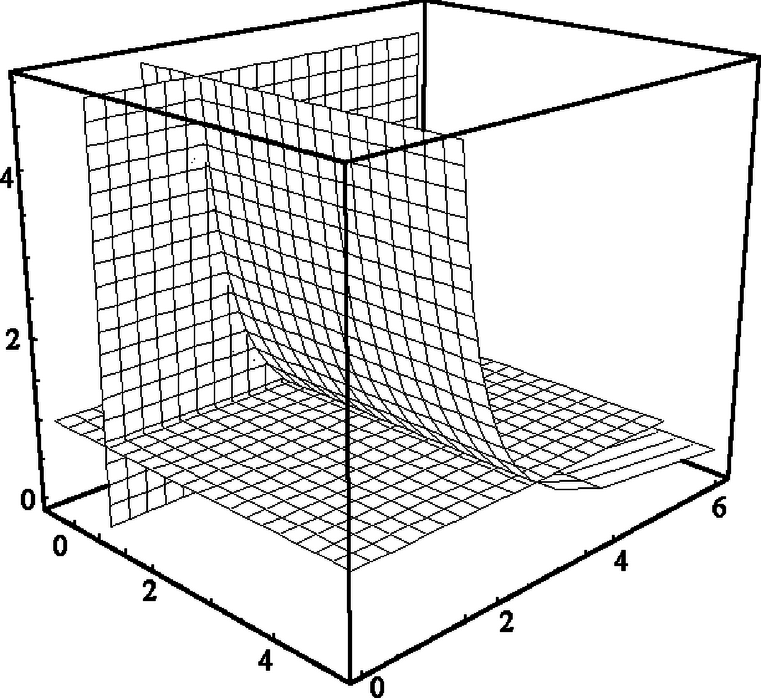

\begin{matrix} \begin{matrix} (1, y, z), & aholy,z > 0racionális számok, \\ (x, y, 1), & aholx \neq 1,x,y > 0racionális számok, \\ (x, {(1 + \frac{1}{n})}^{n}, \frac{n + 1}{n}), & aholxpozitív racionális (x \neq 1),npozitív egész, \\ (x, {(1 + \frac{1}{n})}^{n + 1}, \frac{n}{n + 1}), & aholxpozitív racionális (x \neq 1),npozitív egész. \end{matrix} \end{matrix}

Ezek közül az első két sor nyilvánvaló. Az utolsó két sor az

(x, h (z), z)

alakból származik: a kommutatív esetben ugyanis éppen azt vizsgáltuk meg, hogy racionális

v

mellett

h (v)

mikor racionális. (Itt

v

helyett most

z

a változó.) Ott azt kaptuk, hogy ha

v = \frac{p}{q}

és

p > q > 1

egészek, akkor

h (v)

pontosan akkor racionális, ha

p = q + 1

. Ebből adódik a harmadik sor (

q

helyett

n

-nel felírva, a

q = 1

esetet is megengedve). Végül, ha

v = \frac{p}{q}

továbbra is, de

q > p \geq 1

, akkor a kommutatív esetben talált bizonyítás ‐

p

és

q

szerepének felcserélésével ‐ ugyanúgy elvégezhető, ebből egyetlen lehetséges megoldásként

q = p + 1

adódik. Ezt tartalmazza a negyedik sor. (A

p = q

esettel pedig

z \neq 1

miatt nem kell foglalkoznunk.)

5. ábra

Az egész megoldások a fentiekből származtathatók (a fenti harmadik sorban csak az

n = 1

eset szolgáltat egész értéket, az utolsó sor esetén pedig egyáltalán nincs ilyen

n

\begin{matrix} \begin{matrix} (1, y, z), & aholyészpozitív egészek, \\ (x, y, 1), & aholx \neq 1,xésypozitív egészek, \\ (x, 2, 2), & aholx > 1egész. \end{matrix} \end{matrix}

Lóczi Lajos

matematikus hallgató, ELTE