Cím:	Az 1989. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	1989/november, 360 - 363. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. forduló Kezdők (legfeljebb I. osztályosok)   1. Egy tompaszögű háromszög oldalainak hosszai egész számok és szorzatuk $225$. Mekkorák a háromszög oldalai? 2. Bizonyítsuk be, hogy bármely $x$ számnak a legközelebbi egész számtól való távolsága $\frac{1}{2}-\left|\left\{x\right\}-\frac{1}{2}\right|$. (Ahol $\left\{x\right\}$ jelenti a szám törtrészét, azaz $\left\{x\right\}=x-k$, ahol $k$ a legnagyobb olyan egész, mely $x$-nél nem nagyobb.) 3. Bizonyítsuk be, hogy egy $r$ sugarú körbe írt szabályos tizenkétszög átdarabolható olyan téglalapba, melynek oldalai $r$ és $3r$. 4. Az $1989$ számot különböző természetes számokból akarjuk előállítani, az összeadás és kivonás műveletek kizárólagos alkalmazásával. (Tehát semmilyen más művelet nem alkalmazható, ezeket viszont akárhányszor igénybe vehetjük.) Hány olyan előállítás van, melyben a felhasznált számok számjegyei a 2, 3, 4, 5, 6, 0 számjegyek közül kerülnek ki, és mind a hat számjegy az előállításban pontosan egyszer szerepel? 5. Hányféleképpen tölthettük ki a lottószelvényt, ha az első hatvan számból hat számot a következő módon jelöltünk ki: az elsőnek kijelölt két szám után a harmadik az előző kettő összegének a fele, a negyedik az előző három összegének a fele, az ötödik az előző négy összegének a fele, és végül a hatodik az előző öt összegének a fele? 6. Jelöljük $a_i$-vel az első $i$ pozitív egész szám összegének utolsó számjegyét. Van-e olyan $k$ pozitív egész szám, hogy bármely pozitív $n$-re $a_n=a_{n+k}$? 7. Legyen az $ABC$ háromszög $A$-ból kiinduló súlyvonalának $A$ felöli harmadolópontja $H$. Szerkesszünk olyan két $H$-ból kiinduló félegyenest, amelyek az $AH$ szakasszal együtt a háromszöget három egyenlő területű részre osztják. 8. $A$-ból $B$-be a folyó folyásával szemben elindul egy hajó, ugyanakkor pedig $B$-ből $A$-ba egy csónak, amely útjának $4/11$ részét megtéve találkozik a hajóval. A hajó $B$-ből azonnal visszafordul, és a csónakkal egy időben érkezik $A$-ba. Ha a csónak sebessége (álló vízben) háromszor akkora volna, akkor $1$ óra $42$ perccel hamarabb érne $A$-ba, mint a hajó. Mennyi idő alatt ér a csónak $B$-ből $A$-ba (eredeti sebességével)?   Haladók (II. osztályosok)   1. Határozzuk meg a valós számok halmazának azt a legbővebb részhalmazát, amelyre az $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{\sqrt[]{\sqrt[]{2}\cdot x-x\sqrt[]{x-2}}}{\sqrt[]{\sqrt[]{x}-2}+1}}\end{array}$ függvény értelmezhető. 2. Van-e olyan háromszög, melynek két oldala 1 és 4 cm, valamely két magassága pedig $3$ és $4$ cm hosszú? 3. Hány téglalap jelölhető ki a rajzon látható $4\times 10$-es rács vonalaival? 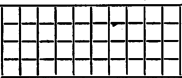    4. A $p$ prímszám (a tízes számrendszerben felírva) páros sok jegyet tartalmaz. Ha a $p$ számot fordított sorrendben írjuk fel, visszakapjuk saját magát. Határozzuk meg $p$-t. 5. Az $ABC$ derékszögű háromszögbe írt négyzet két csúcsa az $AB$ átfogón, másik két csúcsa pedig a befogókon van. Mekkora a befogók aránya, ha a négyzet $K$ középpontjára igaz, hogy $\begin{array}{c}{\displaystyle CAB\sphericalangle =ABK\sphericalangle ?}\end{array}$ 6. Legyenek $x$ és $y$ valós számok. Tudjuk, hogy az $x+y$, $x-y$, $xy$, $\frac{x}{y}$ számok egyike sem 0 és közülük három racionális. Mutassuk meg, hogy $x$ és $y$ racionális számok. 7. Tetszőleges számú egységnyi, illetve két egységnyi oldalú négyzet áll rendelkezésünkre. Bizonyítsuk be, hogy kiválasztható $1987$ darab úgy, hogy belőlük ki lehessen rakni egy négyzetet (hézagtalanul és egyrétűen); viszont bárhogyan is választunk ki $1988$ darabot, azokból sohasem állítható elő négyzet. 8. Az $a$, $b$, $c$ valós számok olyanok, hogy $|a{x}^2+bc+c|\leqq 1$, ha $|x|\leqq 1$. Mutassuk meg, hogy $|x|\leqq 1$ esetén $|c{x}^2-bx+a|\leqq 4$ is teljesül.   II. forduló   Kezdők (legfeljebb I. osztályosok)   A szakközépiskolások feladatai   1. Ábrázolja a számegyenesen a valós számoknak azt a legbővebb részhalmazát, amelyen az $\begin{array}{c}{\displaystyle \frac{x^2+1}{|x-3|}\leqq 1\text{és az}\frac{1}{x+1}>0}\end{array}$ egyenlőtlenségek egyszerre teljesülnek. 2. Adott három egységnégyzet az alábbi elrendezéssel: