Kezdőlap


Cím:	1979. Beszámoló az Eötvös Loránd Fizikai Versenyről
Szerző(k):	Károlyházy Frigyes , Radnai Gyula , Vermes Miklós
Füzet:	1980/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1979. október 27-én rendezte 56. versenyét Budapesten és 11 vidéki városban az 1979-ben érettségizettek és középiskolai tanulók részére. A versenyzők 5 órai munkaidő alatt oldhattak meg három feladatot. Bármely segédeszköz használata megengedett ezen a versenyen, beleértve a zsebszámítógépet is. Összesen 300 dolgozat érkezett be. Ismertetjük a feladatokat és megoldásukat.

1. Egy súlyzó alakú űrállomás körpályán kering a Föld körül. (Hajtóműveit nem működteti.) Az űrállomás tengelye milyen helyzetben maradhat meg változatlanul a mindenkori pályasugárhoz képest?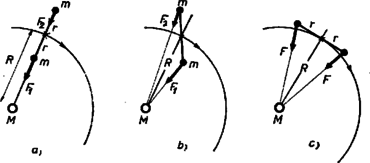

1. ábra

Megoldás. Először helyezzük el az űrállomást a keringés síkjában a rádiuszhoz képest ferde szögben (1.b ábra). A közelebbi tömegre ható

F_{1}

erő nagyobb, mint a távolabbi tömegre ható

F_{2}

vonzóerő, azonkívül

F_{2}

erőkarja is kisebb. Olyan forgatónyomaték keletkezik, amely a rádiuszhoz közelíti a tömegeket. Így nincs egyensúlyi helyzet.
Ha a súlyzó a rádiusz irányában fekszik, nincs forgatónyomaték, az ilyen helyzet egyensúlyi helyzet, méghozzá stabilis. (Ha kibillentenénk az űrállomást ebből a helyzetéből, a fellépő forgatónyomaték a radiális helyzet felé forgatná.) Ez az egyensúlyi helyzet akkor valósul meg, ha olyan

ω_{1}

szögsebességgel helyezzük az űrállomást a körpályára, amely mellett

\begin{matrix} \frac{f m M}{{(R - r)}^{2}} + \frac{f m M}{{(R + r)}^{2}} = m ω_{1}^{2} (R + r) + m ω_{1}^{2} (R - r), \end{matrix}

(a gravitációs erő szolgáltatja a körmozgás gyorsulását).
Eszerint a szükséges szögsebesség:

\begin{matrix} ω_{1}^{2} = \frac{f M}{R} \cdot \frac{1 + {(r / R)}^{2}}{{[1 - {(r / R)}^{2}]}^{2}} \approx \frac{f M}{R^{3}} \cdot [1 + 3 {(\frac{r}{R})}^{2} + ...] . \end{matrix}

Elhelyezhetjük az űrhajót a körpálya érintőjében is (1.c ábra). Ez is egyensúlyi helyzet, mert az eredő forgatónyomaték nulla, de labilis, mert a legkisebb kimozdulás esetében átbillen a radiális helyzetbe. Az érintőleges egyensúlyi helyzet esetében a mozgásegyenlet:

\begin{matrix} \frac{f m M}{R^{2} + r^{2}} = m ω_{2}^{2} \sqrt[]{R^{2} + r^{2}} . \end{matrix}

Ilyen esetben a (labilis) egyensúlyi helyzethez

ω_{2}

szögsebesség tartozik:

\begin{matrix} ω_{2}^{2} = \frac{f M}{R^{3}} \cdot \frac{1}{{[1 + {(r / R)}^{2}]}^{3 / 2}} \approx \frac{f M}{R^{3}} \cdot [1 - \frac{3}{2} {(\frac{r}{R})}^{2} + ...] . \end{matrix}

Ez a szögsebesség kisebb, mint amely a radiális, stabilis egyensúlyi helyzethez tartozik.
Ugyanez a meggondolás érvényes akkor is, ha az űrhajó helyzete merőleges a pályasugárra, de nem fekszik a pálya síkjában.
Megvizsgáljuk az energiaviszonyokat is. A radiális, stabilis egyensúlyi helyzetben a gravitációs energia a végtelenhez képest:

\begin{matrix} - \int_{R - r}^{\infty} \frac{f m M}{x^{2}} d x - \int_{R + r}^{\infty} \frac{f m M}{x^{2}} d x = - \frac{2 f m M}{R} \cdot \frac{1}{1 - {(r / R)}^{2}} \approx - \frac{2 f m M}{R} \cdot [1 + ({\frac{r}{R}}^{2}) + ...] . \end{matrix}

Az érintőleges helyzetben a gravitációs energia:

\begin{matrix} - 2 \int_{\sqrt[]{R^{2} + r^{2}}}^{\infty} \frac{f m M}{x^{2}} d x = - \frac{2 f m M}{R} \cdot \frac{1}{\sqrt[]{1 + {(r / R)}^{2}}} \approx - \frac{2 f m M}{R} \cdot [1 - \frac{1}{2} {(\frac{r}{R})}^{2} + ...] . \end{matrix}

A radiális helyzetben a gravitációs energia alacsonyabb, mint a labilis egyensúlyi helyzetben.

2. Két,

r = 1 cm

sugarú drótkarika

d = 1 cm

távolságban áll egymással szemben. A drótkarikákat szappanhártyák vonják be. Amikor a két hártyát egy elektromos feszültségforrás sarkaira kapcsoljuk, a hártyák gömbsüvegek formájában kissé egymás felé domborodnak. Mindegyik hártya közepének elmozdulása

h = 1 mm

. Mekkora az elektromos potenciálkülönbség? A szappanoldat felületi feszültsége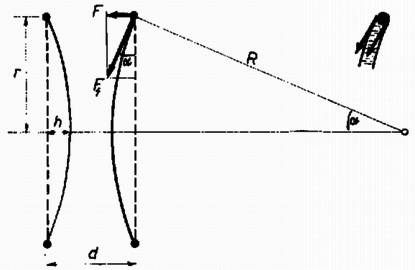

f = 0, 03 newton/méter .

2. ábra

Megoldás. Egy szóródásmentes, homogén terű síkkondenzátor két lemeze között a vonzóerő:

\begin{matrix} F = \frac{1}{2} \cdot \frac{1}{4 π \cdot 9 \cdot 10^{9}} \cdot \frac{A}{d^{2}} \cdot U^{2} . \end{matrix}

Itt az

A = π r^{2}

lemezterület

m^{2}

-ben, a

d

lemeztávolság méterben, az

U

potenciálkülönbség voltban, az

F

erő newtonban értendő. Megoldásunkban a szappanhártyákat síkkondenzátor lemezeiként kezeljük.
A felületi feszültségből a kerület minden hosszegysége mentén

2 f

erő származik, mert a hártyának két oldala van (2. ábra). Ennek az erőnek

2 f sin α

összetevője egyensúlyozza az elektrosztatikus vonzóerőt, a teljes

2 π r

egész kerület mentén összegezve:

2 π r \cdot 2 f sin α

.
A

sin α

a gömbsüveghez tartozó derékszögű háromszögből számítható:

R^{2} = r^{2} + {(R - h)}^{2}

, innen

\begin{matrix} R - \frac{r^{2} + h^{2}}{2 h} és sin α - \frac{r}{R} = \frac{2 h}{r} \cdot \frac{1}{1 + {(h / r)}^{2}} \approx \frac{2 h}{r} . \end{matrix}

Az elektrosztatikus erőt egyenlővé tesszük a felületi feszültségből származó erővel,

sin α

értékét felhasználva:

\begin{matrix} \frac{1}{4 π \cdot 9 \cdot 10^{9}} \cdot \frac{π r^{2}}{d^{2}} \cdot U^{2} = 4 π r f \cdot \frac{2 h}{r}, \end{matrix}

innen a keresett potenciálkülönbség:

\begin{matrix} U = \frac{4 d}{r} \cdot \sqrt[]{4 π \cdot 9 \cdot 10^{9} f h} = 737 volt . \end{matrix}

3. Az első esetben a 3.a ábra szerint az

M

mágnes tengelyére merőleges síkban helyezkedik el az

A

lapos tekercs. A második esetben a mágnes tengelyéhez szimmetrikusan ugyanolyan B tekercs is van (3.b ábra.) A mágnesrudat hirtelen elrántjuk. Melyik esetben lesz nagyabb az

A

tekercsben keletkező áram?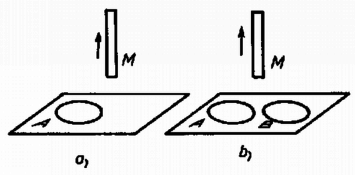

3. ábra

Megoldás. A mágnes elrántásakor csökken az

A

tekercsben az

M

mágnes által okozott fluxus, ezért a tekercsben olyan irányú áram indukálódik, amelynek mágneses fluxusa pótolni igyekszik a fluxusveszteséget. A 4. ábra metszetben mutatja az elrendezést. Az indukált áram által keltett mágneses tér erővonalait a szaggatott körök mutatják. A második esetben az indukált áram által a

B

tekercsben létrehozott erővonalak egy része átmegy az

A

tekercs területén is, de az

A

tekercs indukált áramához tartozó erővonalakkal szembe haladva. Így a

B

tekercs jelenlétében az

A

tekercs indukált áramának nagyobb fluxusváltozást kell kivédenie. Tehát a második esetben nagyobb az

A

tekercs indukált áramának erőssége. Természetesen mindezt fordítva el lehetne mondani

B

tekercsre is.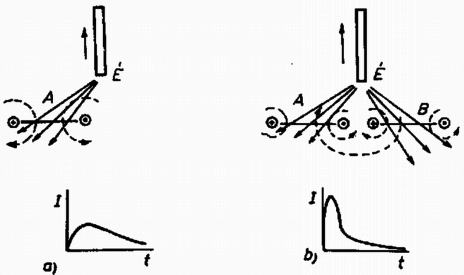

4. ábra

Indukció esetében az összes megmozdított töltés arányos a teljes fluxusváltozással. A teljes fluxusváltazás ‐ a kísérlet elejétől a végéig vizsgálva ‐ mindkét kísérletben ugyanakkora, így a megmozdított töltés is. A 4. ábra alsó részén az

I - t

diagramok alatti területek egyenlők, de a

b

kísérlet esetében az áramcsúcs hegyesebb.

A verseny eredménye

I. díjat nyert Kaufmann Zoltán, a budapesti ELTE-TTK fizikus hallgatója (a váci Sztáron Sándor Gimnáziumban érettségizett Molnár Sándorné tanítványaként).
II. díjat négyen kaptak egyenlő helyezésben: Bene Gyula honvéd (Miskolcon érettségizett a Földes Ferenc Gimnáziumban Zsudel László tanítványaként), Csordás András honvéd (Esztergomban a Dobó Katica Gimnáziumban érettségizett Sipos Imre tanítványaként), Frankhauser József honvéd (Budapesten a József Attila Gimnáziumban érettségizett Tóth Eszter tanítványaként) és Körmendy Péter honvéd (Budapesten a Petőfi Sándor Gimnáziumban érettségizett Szondi Lajos tanítványaként).
III. díjat nyertek egyenlő helyezésben Szalontai Zoltán a törökszentmiklósi Bercsényi Miklós Gimn. IV o. t., (tanára Szalontai László) és Szomor Zoltán a Pécsi Orvostudományi Egyetem hallgatója (a pécsi Nagy Lajos Gimnáziumban érettségizett Tornyos Tivadar tanítványaként).
Két versenvző kapott dicséretet: Boroven József a budapesti Eötvös József Gimnázium III. o. t. (tanára Vargha Balázs) és Pacher Tibor honvéd (Mosonmagyaróvárott a Kossuth Lajos Gimnáziumban érettségizett Gulyás Ferencné tanítványaként.)