Cím:	Háromszögvonal súlypontjának meghatározása (fordította Márki László)
Szerző(k):	Dr. Schröder, E.
Füzet:	1976/december, 195 - 201. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Háromszögvonal súlypontjának meghatározása   Dozent Dr. E. Schröder, Universität Dresden   Az iskolából jól ismert feladat egy háromszög súlypontjának a meghatározása. Ezt úgy végezzük el, hogy berajzoljuk a háromszögbe a súlyvonalakat, ezek egy pontban, a háromszöglap $S$ súlypontjában metszik egymást. A szerkesztést az indokolja, hogy egy háromszögben a csúcsokat a szemben fekvő oldalfelezőpontokkal összekötő szakaszok valóban (mechanikai értelemben is) súlyvonalai a (homogén) háromszöglapnak. Ha ugyanis egy gondolati kísérletben a lapot a háromszög egyik oldalával párhuzamos, keskeny sávokra bontjuk, akkor mindezen sávok felezőpontjai éppen az ehhez az oldalhoz tartozó súlyvonalra esnek. 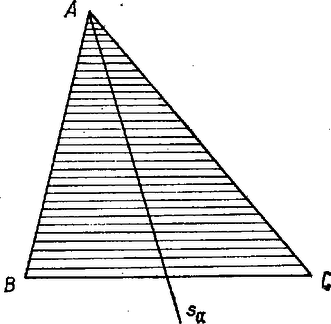    Egy síkidom‐lap két súlyvonalának a metszéspontja éppen a lap súlypontja. Ellenőrzésképpen kivághatunk egy kartonra rajzolt háromszöget, majd az $S$ pontjával vízszintesen ráhelyezhetjük egy fölfelé tartott tű hegyére. Ez a súlypontszerkesztés akkor is helyes, ha háromszögön olyan, három egyenlő tömegű testből álló rendszert értünk, amelyek súlypontjai a háromszög $A$, $B$ és $C$ csúcspontjaiban helyezkednek el. 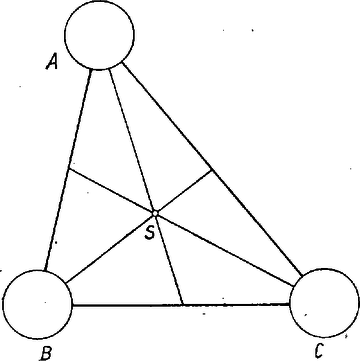    Egészen más meggondolásokra van szükségünk, ha az $ABC$ háromszögben csak a kerület súlypontját akarjuk meghatározni. Ekkor az $ABC$ háromszögvonalról és annak $S_e$ súlypontjáról beszélhetünk. Ehhez megközelítően úgy készíthetünk modellt, hogy három egyforma vastag, ugyanabból az anyagból készült fémrudat háromszög alakú keretté hegesztünk össze. Most könnyen látható, hogy azok az egyenesek, amelyek a háromszög egyik csúcsát a szemközti keretoldal felezőpontjával kötik össze, a keretnek általában nem súlyvonalai. Így aztán ezeknek az egyeneseknek a metszéspontja sem lesz súlypontja a háromszögvonalnak. I. Egy általános háromszögvonal súlypontjának analitikus megközelítéséhez egy könnyen érthető tétel ajánlkozik. Ez a tétel így szól: Forgassunk meg egy egyszerű, zárt, kettős pont nélküli (azaz önmagát nem metsző) $e$ görbét egy olyan $d$ tengely körül, amely a görbe $\epsilon$ síkjában fekszik, de $e$-t nem metszi. Az így keletkezett forgásfelület $F$ felszínét megadja az a szorzat, amelyet egyrészt $e$-nek $l_e$ ívhosszából, másrészt az $e$ görbe $S_e$ súlypontja által egy körülfordulás alatt megtett $l_s$ út hosszából kapunk, vagyis $\begin{array}{c}{\displaystyle F=l_e\cdot l_s\mathrm{.}}\end{array}$ (1) Próbáljuk ki ezt a tételt egy ismert példán! 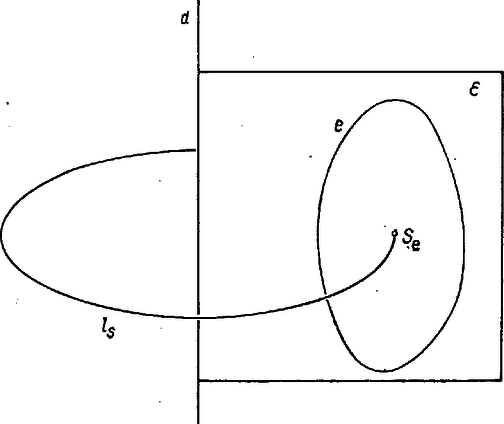    1. Legyen az $e$ zárt görbe olyan téglalap, amelynek a kerülete $l_e=2\left(a+b\right)$. (Sokszögek oldalait és azok hosszát a következőkben ugyanúgy jelöljük: $a$, $b$, $c$, $d$, $\text{...}$ -vel.) A téglalap $a$ hosszúságú oldalának egyikét helyezzük a $d$ forgástengelyre, és forgassuk meg $d$ körül az $e$ téglalapvonalat. 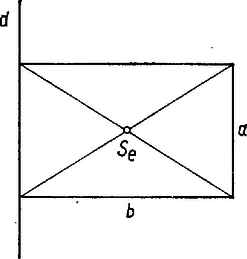    Így hengerfelületet kapunk. A származtató görbe $l_e$ ívhossza most $2\left(a+b\right)$. A négyszögvonal súlypontja $\frac{b}{2}$ távolságra van a tengelytől, ezért a súlypont által egy körülfordulás közben leírt út hossza $\begin{array}{c}{\displaystyle l_s=2\pi \frac{b}{2}=\pi b\mathrm{.}}\end{array}$ A keletkezett henger $F$ felszíne (1) szerint $\begin{array}{c}{\displaystyle F=l_s\cdot l_e=\pi b\cdot 2\left(a+b\right)=2\pi ab+2\pi b^2\mathrm{.}}\end{array}$ A fent idézett tétel tehát, amint azt az ember elvárja, az alap- és a fedőlap valamint a henger palástja területének összegét szolgáltatja. 2. Legyen a megforgatandó $e$ görbe olyan körvonal, amely nem metszi az $\epsilon$ síkban fekvő $d$ egyenest. Ha $\epsilon$-t $d$ körül egyszer körülforgatjuk, akkor $e$ egy tórusznak nevezett gyűrűfelületet ír le. Most ennek a tórusznak a felszínét akarjuk meghatározni. 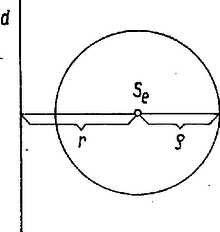    Legyen $e$ sugara $\varrho$, akkor $l_e=2\pi \varrho$. Nyilvánvalóan $e$ középpontja egyben az $S_e$ súlypontja is az $e$-nek. Ha $S_e$-nek $d$-től mért távolsága $r$, és $r>\varrho$, akkor az így keletkezett forgásfelület felszíne (1) szerint $\begin{array}{c}{\displaystyle F=2\pi r\text{...}2\pi \varrho \mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle F=4{\pi }^{2}r\varrho \mathrm{.}}\end{array}$ 3. Most térjünk rá a cikk elején kitűzött problémára. Hogy az $ABC$ háromszögvonal $S_e$ súlypontját meghatározzuk, helyezzük az $a$ oldalt a $d$ forgástengelyre. Ha a háromszögvonalat megforgatjuk a $d$ tengely körül, akkor olyan forgásfelület keletkezik, amely két, közös alapkörű forgáskúpból áll. Az alapkör sugara éppen a háromszög $h_a$ magassága. Eszerint az $A$ csúcs által leírt körvonal hossza $\begin{array}{c}{\displaystyle s=2\pi h_a\mathrm{.}}\end{array}$ Amint azt barkácsolás közben már biztosan észrevettük, forgáskúp palástját kiteríthetjük síkba, és ekkor körcikk keletkezik. Ha ennek a körcikknek a sugara $r$, az íve $s$ hosszú, akkor a körcikk területe $\begin{array}{c}{\displaystyle K=\frac{1}{2}rs\mathrm{.}}\end{array}$ Ha ezt a képletet a mi két kúpfelületünkre alkalmazzuk, ezek területére 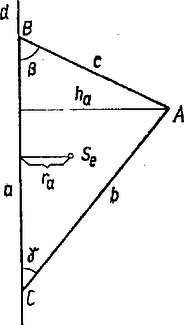$\begin{array}{c}{\displaystyle K_1=\pi h_{a}b\text{és}{K}_2=\pi h_{a}c}\end{array}$ adódik. Mivel $h_a=c\text{sin}\beta =b\text{sin}\gamma$, ezt így is írhatjuk: $\begin{array}{c}{\displaystyle K_1=\pi bc\text{sin}\beta \text{és}{K}_2=\pi bc\text{sin}\gamma \mathrm{,}}\end{array}$ az egész forgásfelület felszíne pedig $\begin{array}{c}{\displaystyle F=K_1+K_2=\pi bc\left(\text{sin}\beta +\text{sin}\gamma \right)\mathrm{.}}\end{array}$ (2) Továbbá ismerjük a megforgatott vonal hosszát: $\begin{array}{c}{\displaystyle l_e=a+b+c\mathrm{.}}\end{array}$ (3)     Jelöljük $r_a$-val az $S_e$ súlypont távolságát az $a$-ra helyezett $d$ forgástengelytől, akkor az egy körülfordulás alatt az $S_e$ által megtett út $\begin{array}{c}{\displaystyle l_s=2\pi r_a\mathrm{.}}\end{array}$ (4) Ha most a fent idézett tételt alkalmazzuk és eközben figyelembe vesszük (1), (2), (3), (4)-et, a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle \pi bc\left(\text{sin}\beta +\text{sin}\gamma \right)=2\pi r_a\left(a+b+c\right)\mathrm{.}}\end{array}$ (5) Itt $r_a$ a keresett mennyiség. Fejezzük ki (5)-ből $r_a$-t: $\begin{array}{c}{\displaystyle r_a=\frac{bc\left(\text{sin}\beta +\text{sin}\gamma \right)}{2\left(a+b+c\right)}\mathrm{.}}\end{array}$ (6) Ebből az eredményből rögtön leolvashatjuk az $S_e$ súlypontnak a másik két háromszögoldaltól mért távolságát is. Ciklikus felcseréléssel ${\displaystyle \begin{array}{cc}\hfill {\displaystyle r_b}& {\displaystyle =\frac{ac\left(\text{sin}\alpha +\text{sin}\gamma \right)}{2\left(a+b+c\right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& \text{(<mn>7</mn>)}\\ \hfill {\displaystyle r_c}& {\displaystyle =\frac{ab\left(\text{sin}\alpha +\text{sin}\beta \right)}{2\left(a+b+c\right)}}\hfill \end{array}}$ adódik. Ezzel számításunk végére értünk. Mutassuk még meg, hogy az így kapott $S_e$ pont általában nem esik egybe a háromszöglap súlypontjával. Annak az általános érvényű állításnak, hogy $S_e$ és $S$ azonos, a megcáfolására elegendő egyetlen ellenpéldát találnunk. Tekintsük azt az esetet, amikor 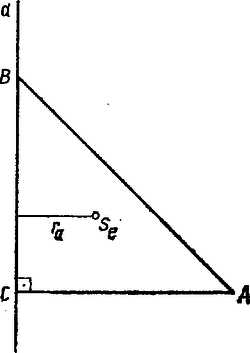$a=b=1$, $c=\sqrt[]{2}$.     Az oldalak ilyen választásával a szögek: $\begin{array}{c}{\displaystyle \beta ={45}^{\circ }\mathrm{,}\gamma ={90}^{\circ }\mathrm{.}}\end{array}$ (6) alkalmazásával azt nyerjük, hogy $\begin{array}{c}{\displaystyle r_a=\frac{1+\sqrt[]{2}}{2\left(2+\sqrt[]{2}\right)}=\frac{\sqrt[]{2}}{4}\mathrm{.}}\end{array}$ (8) Minthogy a háromszög súlyvonalai $1:2$ arányban osztják egymást, azért a háromszöglap $S$ súlypontjának az a oldaltól mért távolsága $\frac{1}{3}$. A két súlypont, $S$ és $S_e$ tehát nem azonos. Csupán egyenlő oldalú háromszög esetében esik egybe a háromszöglap és a háromszögvonal súlypontja. Paul Guldin (1577‐1643) svájci matematikus egy művében szerepelt először az a tétel, amelyet itt a háromszögvonal súlypontjának meghatározására használtunk. A szakirodalomban ezt a tételt az első Guldin‐szabálynak nevezik. A bizonyításra itt nem térhetünk ki. II. Végezetül megmutatjuk, hogyan lehet egy $ABC$ háromszögvonal $S_e$ súlypontját megszerkeszteni. Itt az igen fontos, hogy két "súlyvonalat'' lehetőleg egyszerűen meg tudjunk keresni. Most meghatározzuk az $a$ oldal $P$ felezőpontján átmenő $s_p$ "súlyvonalat''. Ehhez ajánlkozik, hogy megszerkesztünk még egy $X\in s_p$ pontot, mégpedig azt, amelyik a $b$, ill. $c$ oldal $Q$, ill. $R$ felezőpontját összekötő egyenesen fekszik. E célból rendeljünk a $Q$ ponthoz $m_b$, az $R$ ponthoz $m_c$ tömeget úgy, hogy ezek aránya 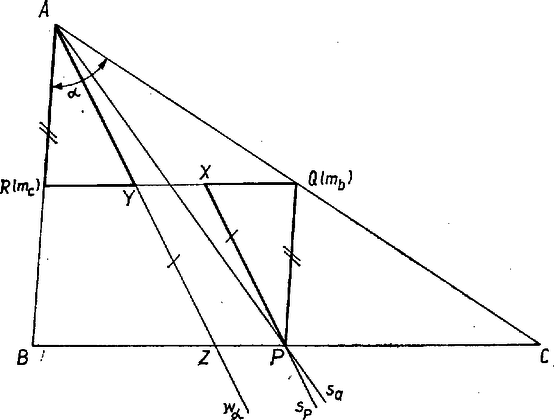$\begin{array}{c}{\displaystyle m_b:m_c=b:c}\end{array}$ (9) legyen. A keresett $X$ pontnak meg kell egyeznie az $m_b$ és az $m_c$ tömegből álló rendszer súlypontjával. Az emelőszabály szerint ha egy két karú emelő egyensúlyi helyzetben van, akkor az emelőkarok hossza a végpontjukba helyezett tömegekkel fordítottan arányos. Az $X\in s_p$ pontra tehát a következő aránynak kell teljesülnie: $\begin{array}{c}{\displaystyle |RX|:|QX|=m_b:m_c\mathrm{.}}\end{array}$ (10) (9) szerint most az $X\in s_p$ meghatározása egy geometriai feladatra vezethető vissza. (10)-zel ekvivalens ugyanis az $\begin{array}{c}{\displaystyle |RX|:|QX|=b:c}\end{array}$ (11) feltétel, ez pedig azt sugallja, hogy a $w_{\alpha }$ szögfelezőt használjuk fel a szerkesztéshez. Rajzoljuk be az $ABC$ háromszögbe az $\alpha$ szög $w_{\alpha }$ szögfelezőjét, és jelöljük ennek a szemközti oldallal, ill. a $\left(QR\right)$ egyenessel alkotott metszéspontját $Z$-vel, ill. $Y$-nal.     Most alkalmazzuk azt a tételt, amely szerint a szögfelező a szemközti oldalt az őt közrefogó oldalak arányában osztja ketté. Ezt a tételt a mi esetünkre alkalmazva azt kapjuk, hogy $\begin{array}{c}{\displaystyle b:c=|CZ|:|BZ|\mathrm{.}}\end{array}$ Minthogy a $\left(BC\right)$ egyenes párhuzamos a $\left(QR\right)$ egyenessel, azért alkalmazhatjuk a párhuzamos szelők tételét. Eszerint $\begin{array}{c}{\displaystyle |CZ|:|BZ|=|QY|:|RY|\mathrm{,}}\end{array}$ így $\begin{array}{c}{\displaystyle |QY|:|RY|=b:c\mathrm{.}}\end{array}$ (12) Most a következőt állítjuk: Ha $P$-n át párhuzamost húzunk $w_{\alpha }$-val, akkor ez a $\left(QR\right)$ egyenest a keresett $X$ pontban metszi; más szóval, ez a $P$-n átmenő, ${\omega }_{\alpha }$-val párhuzamos egyenes éppen a háromszögvonal egyik súlyvonala. Bizonyítás: A szerkesztés szerint $\begin{array}{c}{\displaystyle PQX▵\cong ARY▵\mathrm{.}}\end{array}$ Ezért $\begin{array}{c}{\displaystyle |QX|=|RY|\text{és}|QY|=|RX|\mathrm{.}}\end{array}$ Innen a következő arányt kapjuk: $\begin{array}{c}{\displaystyle |QX|:|RY|=|RX|:|QX|\mathrm{.}}\end{array}$ (13) (12) és (13) alapján ebből következik $\begin{array}{c}{\displaystyle |RX|:|QX|=b:c}\end{array}$ és $\begin{array}{c}{\displaystyle |RX|:|QX|=m_b:m_c\mathrm{.}}\end{array}$ (14) (14)-gyel beláttuk, hogy a fenti szerkesztés teljesíti a (10), és így a (11) feltételt. Ahogy itt az $s_p$ súlyvonalat megszerkesztettük, ugyanúgy szerkesztjük meg a $Q$-ból és az $R$-ből kiinduló súlyvonalat is. Az $ABC$ háromszögvonal keresett súlypontja éppen két, így megadott súlyvonal metszéspontja. Mindezt összefoglalva: Egy háromszögvonal $S_e$ súlypontját a következő eljárással szerkesztjük meg: Az $ABC$ háromszögben megszerkesztjük a három szögfelezőt: $w_{\alpha }$, $w_{\beta }$, $w_{\gamma }$-t, valamint a három oldal, $a$, $b$ és $c$ felezőpontját, $P$, $Q$, $R$-et. Ekkor a $P$-n át $w_{\alpha }$-val, a $Q$-n át $w_{\beta }$-val és az $R$-en át $w_{\gamma }$,-val párhuzamosan húzott három egyenes, $s_p$, $s_q$, ill. $s_e$ egy pontban metszi egymást. Ez az $S_e$ pont a háromszögvonal súlypontja. 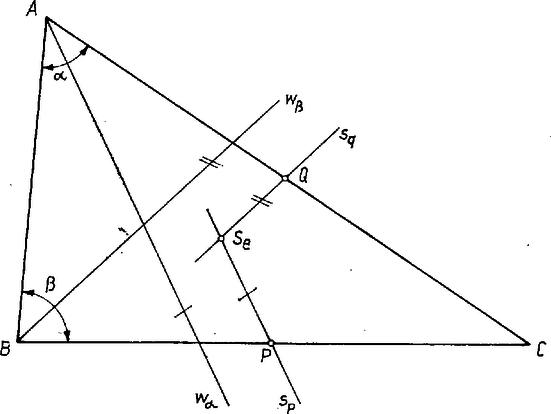    Függelék:   A fenti cikkhez felhasználtuk a következő segédtételt: Egy háromszög bármelyik szögfelezője a vele szemközti oldalt az őt közrefogó oldalak arányában osztja. 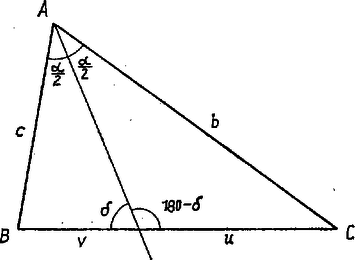    Bizonyítás: Alkalmazzuk a részháromszögekre a szinusz‐tételt! Eszerint $\begin{array}{c}{\displaystyle \frac{\text{sin}\delta }{\text{sin}\frac{\alpha }{2}}=\frac{c}{v}\mathrm{,}\frac{\text{sin}\left({180}^{\circ }-\delta \right)}{\text{sin}\frac{\alpha }{2}}=\frac{b}{u}\mathrm{.}}\end{array}$ (*) Mivel $\text{sin}\delta =\text{sin}\left({180}^{\circ }-\delta \right)$, azért (*)-ból következik, hogy $\begin{array}{c}{\displaystyle \frac{c}{v}=\frac{b}{u}\mathrm{,}\text{azaz}\frac{b}{c}=\frac{u}{v}\mathrm{.}}\end{array}$