Kezdőlap


Cím:	A méhek lépsejtjeiről - matematikus szemmel
Szerző(k):	Csákány Béla
Füzet:	1971/november, 109 - 117. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Megfigyelve a lépet, melyet a méhek az összegyűjtött méz elraktározása és az ivadékok felnevelése céljára viaszból építenek, azt látjuk, hogy az megközelítőleg egybevágó sejtekből áll. A sejtek alakja szabályos hatszög alapú egyenes hasáb, amelynek egyik alapja hiányzik ‐ ez a bejárati nyílás a másik alapját pedig három egybevágó rombuszból álló zárólap-rendszer helyettesíti (1. ábra).

1. ábra

A sejtek két rétegben helyezkednek el, s az ugyanazon rétegben levő sejtek oldallapjaikkal illeszkednek egymáshoz és bejárati nyílásuk síkja közös, a különböző rétegben levők pedig rombusz alakú zárólapjaikkal (2. ábra). Az illeszkedés hézagmentes, tehát a sejtek lapjai (a lép szélén elhelyezkedő lapok kivételével) két szomszédos sejt közös lapjául szolgálnak. (A sejtek állása a méhkasban a 2. ábra szerinti, a lép határoló síkjai körülbelül függőlegesek; ha viszont a matematikus egyetlen sejtet ragad azt természetesen az 1. ábrán látott módon állítja maga elé.)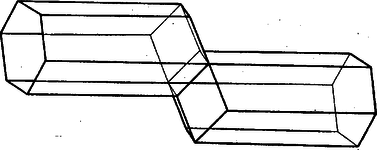

2. ábra

A lépsejtek közepes mélysége

11, 3 mm

, az alap-hatszög élhossza

2, 7 mm

(esetenként kis eltérések vannak), vagyis a sejtek mélysége kb.

2

-szer akkora, mint az alapidom átmérője.
A méheket a takarékosság mintaképének szokás tekinteni, kézenfekvő hát a kérdés, ,,gazdaságosan'' bánnak-e a viasszal a sejtépítésben. Matematikus gondolkodással mindjárt így egyszerűsítenénk a kérdést: mennyi viasz felhasználásával tudnak adott mézmennyiség elraktározásához elegendő sejtet építeni. Más szóval: adott térfogat mellett mekkora a sejt felszíne ? Minél kisebb a felszín, annál gazdaságosabb a méz tárolása.
Arra gondolni, hogy egyetlen tartály esetén a gömb a leggazdaságosabb alak erre a problémára, csak azért érdemes, hogy rádöbbenjünk: egészen máshogyan kell hozzányúlnunk a kérdéshez. Hiszen a méhcsaládnak igen nagy számú kicsi sejtre van szüksége, és ösztönük a sejt alakjának, méreteinek kialakításában nyilván más, biológiai, fizikai adottságokhoz is alkalmazkodott. (Pl. a királynő-nevelő sejtek nagyobbak, teherbírás stb.) Az ilyenek elemzése természetesen nem a matematikus dolga, viszont nem volna dialektikus, ha tudomást sem vennénk róluk. Próbáljuk ezért először az adott helyzetet nagyjából megérteni, mielőtt számításba kezdenénk.
A sejtek egymás közti egybevágóságával (csak a dolgozókat nevelő és méztároló sejtekre gondolva), konvexségével ‐ az ő ,,nyelvükön'' mondva azzal az ösztönös törekvéssel, hogy az építésben minél több egyformaság nyilvánuljon meg ‐, továbbá a sejtfalak kétoldali kihasználásával megmagyarázható, hogy a falak csak síklapok lehetnek. Hozzávéve, hogy minden sejthez külön bejárat kell, éspedig csak egy, adódik a lép kétrétűsége és a cellák nagyjából hengeres, hasábos, egy fejlődő méh testét éppen befogadó alakja, a párhuzamos határlapok, mert így a sejtek határfelületének a nyílástól legtávolabbi részei ‐ a mondott zárólapok ‐ szintén kétszeresen vannak kihasználva.
Az egyes sejtek szimmetriája, részletezve: lapjainak egybevágósága és a találkozó lapok kölcsönös helyzetének egyformasága is megérthető az építés egyszerűségéből, ezért egyenlők az alapidom oldalai és szögei, ezért derékszögek az alapon levő lap és élszögek. Végül abban, hogy a szabályos sokszögnek kikövetkeztetett alapidomnak éppen hat oldala van, azt látjuk érvényesülni, hogy a síkot egyrétűen és hézagtalanul, egybevágó, szabályos sokszögekkel lefedni csak úgy lehet, ha a sokszög oldalainak száma

3

4

vagy

6

, és e három idom közül rögzített terület esetén éppen a szabályos hatszögnek van legkisebb kerülete.
Ezek alapján a továbbiakban adottságnak tekintjük, hogy a lépsejtek szabályos hatszög alapú egyenes hasábok ‐ legalábbis a bemeneti részük ilyen alakú ‐ és figyelmünket a zárólapok alakjára és elhelyezkedésére fordítjuk.
2. Meggondolásaink egy része elemi geometriai jellegű, másrészt alkalmazni fogjuk a differenciálszámítás elemeit is. Eközben egyes részletek bővebb átgondolását az olvasóra hagyjuk.
Tekintsünk egy

A B C D E F

szabályos hatszög fedőlapú egyenes hasábot (3. ábra).

Alapélét egységnek vesszük,

A A'

oldalélének hosszúságát

a

-val jelöljük. Térfogata ekkor

\frac{3 \sqrt[]{3}}{2} a

. Metsszük le hasábunkról az

A

C

és

X

pontokon átmenő síkkal az

A X C B

tetraédert s forgassuk el

180^{\circ}

-kal

A C

mint tengely körül. Ekkor a

B

csúcs a hatszög

O

középpontjába kerül, az

X

csúcs az

O

-ban emelt merőleges egy

P

pontjába s az

A

X

C

P

pontok egy rombusz csúcsai lesznek. Válasszuk meg ezután

Y

-t az

F F'

Z

-t a

D D'

oldalélen úgy, hogy

F Y = D Z = B X

, és járjunk el hasonlóan az

E Y A F

és

E Z C D

tetraéderrel. Az elforgatás után

F

és

D

megy át

O

-ba,

Y

és

Z

pedig

E

-be.
Az így keletkezett síklapú testet nevezzük lépsejtidomnak. Ennek zárólapjai az

A X C P

E Y A P

és

C Z E P

rombuszok, és térfogata megegyezik az eredeti hasábéval. Felszínéről viszont azt sejtjük, hogy kisebb, mint az eredeti hasábé.
Vezessük be a

B X = x

jelölést és kérdezzük:

x

mely értéke mellett lesz a lépsejtidom felszíne minimális. (Megjegyezzük, hogy

x

változtatásával a zárólaprendszer minőségileg nem változik, hacsak

0 < x \leq a

, csupán a rombuszlapok síkjai fordulnak el a végzett forgatások tengelyei körül. Szokásos kifejezéssel: egy szabadsági fokunk van a változtatásra: a zárólapok szögének változtatása.) A felszínt megadó

\begin{matrix} F (x) = 6 a - 3 x + 3 \sqrt[]{3 x^{2} + \frac{3}{4}} \end{matrix}

függvénynek csak ott lehet minimuma, ahol derivált függvénye a

0

értéket veszi fel. Mármost az

\begin{matrix} F' (x) = 3 (- 1 + \frac{3 x}{\sqrt[]{3 x^{2} + \frac{3}{4}}}) = 0 \end{matrix}

egyenlet egyetlen (pozitív) megoldása

x = \frac{\sqrt[]{2}}{4}

. Megmutatjuk, hogy

F' (x)

monoton növekvő (természetesen csak az

x > 0

értékeket tekintjük). Ugyanis azonos átalakításokkal

\begin{matrix} F' (x) = 3 (\frac{3}{\sqrt[]{3 + \frac{3}{4 x^{2}}}} - 1), \end{matrix}

x

növekedésével a

\frac{3}{4 x^{2}}

tag és vele az egész nevező csökken, a tört és vele

F' (x)

is nő. Ámde az

x = 0

helyen (az eredeti alakból)

F' (0) = - 3

, és mint tudjuk,

F' (\frac{\sqrt[]{2}}{4}) = 0

, és utána tovább nő, vagyis a

\frac{\sqrt[]{2}}{4}

helyen

F' (x)

negatívból pozitívba megy át, és ennek megfelelően

F (x)

csökkenésből növekedésbe megy át. Így az

x = \frac{\sqrt[]{2}}{4}

helyen

F (x)

-nek valóban minimuma van, és ott van az egyetlen minimuma, amelynek értéke

F (\frac{\sqrt[]{2}}{4}) = 6 a + \frac{3 \sqrt[]{2}}{2} = 6 a + 2, 1213

területegység.
3. Most már több érdekeset mondhatunk az optimális (legkisebb felszínű) lépsejtidomról.

x = \frac{\sqrt[]{2}}{4}

esetén egyszerű számításokkal a rombuszlap oldala

A X = \frac{3 \sqrt[]{2}}{4}

‐ éppen

3 x

‐, átlói

P X = \frac{\sqrt[]{6}}{2}

és

A C = \sqrt[]{3}

, ezekből területe

\frac{3 \sqrt[]{2}}{4}

, vagyis mértékszámban egyenlő

A X

-szel, tehát a rombuszlap magassága (szélessége)

1

. Ez ismét ugyanannyi, mint a hasáb oldallapjainak szélessége, más szóval

X

-nek

P A

-tól és

A A'

-tól való távolsága egyenlő. (A 3. ábrán jobb áttekintés érdekében

x

-et jóval nagyobbnak vettük, mint az optimális

0, 354

érték.) Ebből és a lépsejtidom (forgási és tükrözési) szimmetriáiból következik, hogy idomunk

A

(valamint

C

és

E

) csúcsánál összefutó

4

él szomszédos párjai közti szögek egyenlők; mindegyik hegyesszög, mert a

P A X C

lapban

P X < A C

. Továbbá az is következik, hogy

3 - 3

egyenlő tompaszög (az előbbiek kiegészítő szöge) fut össze a

P

X

Y

Z

csúcsokban.
Ezek szerint lehet úgy forgatni az optimális lépsejtidomot egy, az

X

csúcsán átmenő tengely körül, hogy

A

C

-be jusson, az

X C

egyenes az

X B'

élre és

X B'

X A

egyenesre (így az

A A'

él a

C P

egyenesre fordul rá). Ez ‐ továbbmenve ‐ azt jelenti, hogy a

P A X C

rombuszlap ugyanakkora szöget zár be az

A X B' A'

oldallappal, mint ez a

C X B'

oldallappal, vagyis

120^{\circ}

-ot. Eszerint az optimális lépsejtidom

15

éle mindegyikénél az ott összefutó

2 - 2

lap

120^{\circ}

-os szöget zár be egymással.
A mondott forgatást még

2

-szer ismételve az

X A

X C

X B'

élek visszajutnak eredeti helyzetükbe, tehát a forgatás szöge is

120^{\circ}

volt.
Azt is könnyű belátni, hogy lépsejtidomunk egybevágó példányaival hézagtalanul és átfedés nélkül ki lehet tölteni a térnek olyan sávját, melyét két párhuzamos sík határol egymástól

2 a

távolságban. Toljuk el a

P A X C Z E Y A' B' ... F' = S

sejtidomot az

\vec{E C}

vektorral az

S_{2}

helyzetbe.

\vec{E A}

-ral az

S_{3}

-ba; a 4. ábrán a határsíkokra merőleges irányból nézve látjuk ezt a helyzetet, minden jelzőbetű

2

-es, illetve

3

-as indexet kapott az új helyzetben, egyes ilyen pontok már a 3. ábrán is fel vannak tüntetve. Ekkor

Y_{2} E_{2}

egybeesik

X C

-vel és

Z_{3} E_{3}

X A

-val,

S_{2}

és

S_{3}

egy-egy trapézlap mentén hézagtalanul illeszkedik

S

-hez és egymáshoz, az

X B'

él mentén a tér ki van töltve. Továbbá az

X \equiv Y_{2} \equiv Z_{3}

pontban a három sejtidom egy-egy rombuszlapja fut össze tompaszögű csúcsával. Ha tehát

S

-et elfordítjuk

A C

mint tengely körül,

180^{\circ}

-kal, az így kapott

S_{4}

-nek

P_{4}

csúcsa is

X

-be jut (továbbá

X_{4}

Y_{4} Z_{4}

csúcsa rendre a

P

-be,

P_{3}

ba,

P_{2}

-be) és a tér

P_{4}

körül is ki van töltve. A további kitöltésben természetesen az

\vec{A C}

-t is bevesszük transzlációs vektornak és az eddigi vektorok

(- 1)

-szereseit is, és ugyanezekkel toljuk el

S_{4}

et is. ‐ Ez a záródás ‐ kitöltés nincs kötve

x

-nek optimális értékéhez, érvényes bármely

0 < x \leq a

érték mellett.
Hasznos lesz a továbbiak szemléletének könnyítésére eredményünket az alábbiak szerint is elmondani. A térsávot kitöltő sejtidomrendszer úgy keletkezett, hogy először a 3. ábra kiindulási hasábján végeztük el a legutóbb leírt eltolásokat, forgatásokat. Így a térsáv hézagtalanul és átfedés nélkül van kitöltve, felezősíkjában az egyik réteg minden egyes lapközéppontjával egybeesik a másik réteg három egymáshoz csatlakozó hasábjának közös csúcsa, például

O_{4}

-gyel

B

F_{2}

és

D_{3}

, az

O

-val egybeesők egyike pedig

B_{4}

. Továbbá egy alsó és egy felső rétegbeli hasáb véglapjainak közös része egy egységnyi oldalú,

60^{\circ}

szögű rombusz, például

A B C O

, illetve a fölötte levő hasábról

A_{4} O_{4} C_{4} B_{4}

. Ezután ,,térrész átcsatolásokat'', cseréket hajtottunk végre a két réteg így érintkező hasábtartománypárjai között. Kettévágtuk például a most mondott rombuszt

A C = A_{4} C_{4}

átlója mentén és ezen át levágtuk a két hasábról a

B X = B_{4} X_{4} = x

magasságú

A C B X

A_{4} C_{4} B_{4} X_{4}

tetraédereket és hozzácsatoltuk mindegyiket a másik (megcsonkított) hasábtartományhoz. Ugyanezt végeztük minden olyan ‐ egy alsó és egy felső rétegbeli hasábból álló ‐ pár között, melyeknek van közös véglap-része. Így minden hasábról

3

tetraédert csonkítottunk le és

3

másikat csatoltunk hozzá, az utóbbiak egyesítve egy, az

A C E P

-vel egybevágó tetraédert adnak. Minden hasábos tértartomány ugyanannyi térfogatot kapott a másik rétegbeli

3

szomszédjától, mint amennyit azoknak átadott, így a sejtidomtartományok térfogata egyenlő az eredeti hasábtartományokéval, és természetesen a térsáv most is hézagtalanul és egyrétűen van kitöltve.
4. Visszatérve most már eredeti kérdésünkhöz, a lépsejtidomunk lapjaiban levő szögekre,

X A P ∢ = X A A' ∢ = α

jelöléssel az

A X = 3 x = 3 B X

észrevételből

cos α = 1 / 3

α = 70^{\circ} 32'

, ez tehát az optimális lépsejtidomon levő

6

trapéz és

3

rombuszlapnak a hegyesszöge.
Mivel ez a hegyesszög a lépsejtidom alakját egyértelműen meghatározza, elegendő ezt összehasonlítani a valóságos lépsejt megfelelő szögével. A méheknél ezt a hegyesszöget kb.

70^{\circ}

-nak találjuk, ennél pontosabb megmérésnek nem is volna értelme, mivel a puha viaszból kialakított sejtekben az élek és a csúcsok természetesen kissé legömbölyítettek. Így érthető az az igen elterjedt nézet, hogy a méhek sejtjeik zárólapjait a leggazdaságosabb módon építik meg. ^{$^{*}$}
5. Ezt a vélekedést 1964-ben Fejes-Tóth László megcáfolta. ^{$^{*}$} Gondolatmenetét a következőkben ismertetjük, előkészítésül azonban egy másik utat mutatunk arra, hogyan lehet eljutni a méhek lépsejtidomához.
Tekintsünk egy kockát, s minden egyes lapjára illesszünk egy vele egybevágó kockát úgy, hogy az illeszkedő lapok egybeessenek (5. ábra bal oldali része), majd vegyük egy konvex síklapú test csúcsaiul az eredeti kocka

8

csúcsát, meg a további

6

kocka középpontját (az ábra jobb oldali része).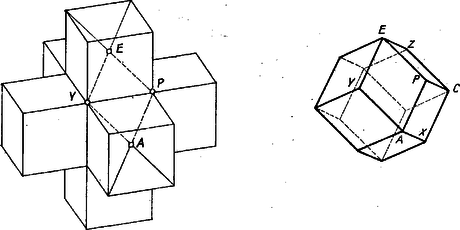

5. ábra

Ezt a testet ‐ mivel

12

(görögül: dodeka) lapja van s ezek mind egybevágó rombuszok ‐ rombdodekaédernek szokás nevezni. Két olyan csúcs, mint az ábrán

A

és

C

, két szomszédos kockalapon illeszkedő kockák középpontjai, akkora távolságban van egymástól, mint a kocka egy lapjának átlója ‐ az ábrán például

Y Z

, így a

P A X C

rombuszlap két átlójának aránya

\sqrt[]{2}

, akárcsak a méhek rombuszainál a

\sqrt[]{3} : \frac{\sqrt[]{6}}{2}

arány, tehát a rombdodekaéder lapjai hasonlóak a fent talált optimális lépsejtidom rombuszaihoz. További egyezés az 5. és 3. ábrák között, hogy a rombdodekaéderen is az eredeti kockacsúcsokban (mint

P

)

3 - 3

rombusz fut össze a tompaszögével ‐ más szóval a rövidebb átló végpontjávál ‐, a hozzáillesztett kockák középpontjaiban pedig (mint

A

)

4 - 4

rombusz hegyesszöge, hosszabbik átlója találkozik.
Ezek szerint, ha egy

\frac{\sqrt[]{6}}{2}

élű kockából kiindulva alkotunk rombdodekaédert, ebből elhagyjuk azt a

3

lapot, amely a kocka

P

-vel szemben fekvő csúcsában fut össze, a

P A Y E

P E Z C

P C X A

lapokhoz az

A X C Z E Y A

,,koronavonal'' mentén csatlakozó

6

rombuszlapot pedig a csatlakozási éllel szemben levő él távolításával ,,folytatjuk'', akkor éppen az optimális lépsejtidomhoz jutunk. (A lépben a

P

-ből induló kockaátló fordul vízszintesre.)
Erre támaszkodva Fejes-Tóth László felvetette: van-e más olyan síklapú test is, amelynek

6

lapját alkalmas módon folytatva, egyes lapjait viszont elhagyva, szabályos hatszög alapú egyenes hasábot kapunk, egyik végén olyan zárólaprendszerrel, amely alkalmassá teszi arra, hogy ‐ a lépsejtidomhoz hasonlóan ismételve ‐ két rétegben hézagmentesen elhelyezhessük, s emellett a kapott idom felszíne ‐ változatlan térfogat mellett ‐ kisebb, mint a lépsejtidomé.
Fejes-Tóth László leírt egy ilyen testet. Vett két olyan egybevágó szabályos négy oldalú gúlát, amelyeknél az oldallap magassága egyenlő az alapéllel, ezeket alapjaikkal összeillesztette, majd a kapott kettős gúlának ‐ ami a szabályos oktaéderből is előállítható, egyik csúcstengelyével párhuzamos,

\sqrt[]{3 / 2} = 1, 22

arányú nyújtással ‐ mind a

6

csúcsát ,,lecsonkította'', a szemben levő csúcspárokat összekötő

3

tengelyre merőleges síkokkal (6. ábra).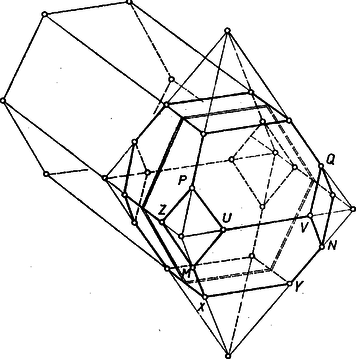

6. ábra

A kiindulási gúlák (négy élű) csúcsait eltávolító síkok félmagasságban metszik a gúlákat, negyedelik a tengelyt, felezik a végpontjaiba befutó

4 - 4

élt. A további

4

csúcsot levágó síkok pedig a csúcsoktól számított első nyolcadoló pontjukban metszik az illető (a fő tengelynél rövidebb) tengelyt, vagyis negyedelik az eredeti kettős gúlának az illető csúcsban összefutó éleit, és így a kettős csonka gúla oldaléleit felezik (ugyanis a kettős gúla bármelyik csúcstengelyét véve; a többi

4

csúcs egy síkban van).
Az így nyert testnek

14

lapja van, páronként párhuzamosak, a test szimmetrikus az összeillesztési síkokra és az egyes gúlák szimmetriasíkjaira (

4

sík). Megtartva belőle azt a

4

lapot, amely az egyik összeillesztési alapélen keletkezett

U

V

negyedelő pontokban fut össze (

2

hatszög és

2

rombusz), elhagyva az ezekkel párhuzamos

4

lapot és folytatva a további

6

lapot, előttünk áll a kívánt alak, nevezzük ezt négyzárólapú sejtidomnak.
Valóban, idomunk meghosszabbított lapjai egy szabályos hatoldalú hasáb oldallapjai, mert a kettős gúlából bármelyik alapélének

σ

felező merőleges síkja

60^{\circ}

szögű rombuszt metszett ki, ebből az első két csonkító sík szabályos hatszöget hagy vissza és a meghosszabbított

6

lap mindegyike merőleges

σ

-ra. (A

14

lapú test tulajdonképpen két egybevágó szabályos hatoldalú hasáb közös része, melyeknek tengelyei merőlegesen metszik egymást és két párhuzamos lappárjuk síkja közös.)
A négyzárólapú sejtidom felszínének és térfogatának megállapításához megmutatjuk, hogy idomunk, a kiindulási gúlák alapélét

2

egységnyinek véve ‐ a háromzárólapú sejtidomnál (3. ábra) látott lemetszésekhez és elforgatásokhoz hasonlóan ‐ előállítható az

a

magasságú,

1

alapélű szabályos hatoldalú hasábból. Legyen ugyanis

M

N

P

Q

sorban a hasáb

F A

B C

F E

D C

fedőélének felezőpontja, továbbá mérjük fel az

A

-ból,

B

-ből,

F

-ből induló oldalélre az

A X = B Y = F Z = 1 / 4

szakaszt (7. ábra,

A X

nagyítva).

7. ábra 8. ábra

Csonkítsuk le az

A B

élt az

M

N

X

(és

Y

) pontokon átmenő síkkal, az

F

csúcsot az

M P Z

síkkal, és forgassuk el

180^{\circ}

-kal a lemetszett

M A X N B Y

ötlapú testet

M N

mint tengely körül, a

P M F Z

tetraédert

P M

körül. Ekkor

A

és

B

F C

átló első, illetve harmadik negyedelő pontjába jut,

F_{1}

be, illetve

C_{1}

be, hiszen

F C = 2 A B = 2 X Y

, az

F

csúcs ugyancsak

F_{1}

be, másrészt

X

és

Z

F_{1}

fölött egyesülnek

U

-ban, ahol

F_{1} U = A X = 1 / 4

, az

Y

csúcs pedig a

C_{1}

fölé jut.
Járjunk el hasonlóan a

D E

éllel, a

C

csúccsal, és forgassuk el

180^{\circ}

-kal a lemetszett, az előbbiekkel rendre egybevágó testeket

P Q

, illetve

Q N

körül, így

E

F_{1}

-be,

D

és

C

C_{1}

-be jut, a testek új csúcsai pedig

U

-ba,

V

-be.
Az így kapott zárólaprendszer két lapja az

M X Y N V U

két szimmetriatengelyű hatszög és az

M Z P U

rombusz, a másik kettő ezek tükörképe, hiszen a rendszer nyilvánvalóan szimmetrikus az

F C

és

A E

átlók felező merőleges síkjára nézve. A hatszögben

M N = 3 / 2

és

X Y = X U = 1

, a további élek

M X = M U = M Z = \sqrt[]{5} / 4

, végül a rombusz átlói

M P = \sqrt[]{3} / 2

Z U = \sqrt[]{2} / 2

és ugyanezeket az értékeket kapjuk a 6. ábrán látott, előre ugyanígy betűzött test lapjainak méreteire.
Ezek szerint a négyzárólapú sejtidom térfogata annyi, mint a kiindulási hasábé. Zárólaprendszerének és palástjának felszíne

\begin{matrix} 2 [(1 + 2 \cdot \frac{1}{8}) + \frac{\sqrt[]{2} \cdot \sqrt[]{3}}{8}], illetve 2 (a - \frac{1}{4}) + 4 (a - \frac{1}{8}), \end{matrix}

együttvéve

\begin{matrix} 6 a + \frac{3}{2} + \frac{\sqrt[]{6}}{4} = 6 a + 2, 1124 \end{matrix}

területegység, kisebb, mint a háromzárólapú sejtidom felszíne (azonos térfogat mellett).
Hátra van még a két párhuzamos sík közti térsáv kitöltésének bizonyítása a négyzárólapú sejtidommal. A korábban végzett térrész-átcsatolási meggondolásunkon az iménti csonkítási és forgatási lépéseinkhez igazodva, csak kis módosítást kell végeznünk: a felső réteget az alsóhoz képest másképpen kell elhelyeznünk, mint az 5. ábra esetében, hiszen az iménti csonkítások és elforgatások lényegében négy átcsatolást, cserét jelentenek. A 7. ábra

M A B N

trapéza

M F_{1} C_{1} N

-be került át, vagyis

A B

F_{1} C_{1}

be, eszerint az alsó rétegbeli oldalfalak eddigi alaprajzából úgy készül a felső réteg alaprajza, hogy azt az

\frac{\vec{A E}}{2}

vektorral toljuk el (8. ábra). Ezáltal a térkitöltés is felveszi a négyzárólapú sejtidom szimmetriáját:

2

tükörsíkrendszere van egymásra merőleges síkállásokkal, szemben a méhek

3

tükörsík állásával.
A Fejes-Tóth-féle sejtidom tehát gazdaságosabb az optimális lépsejt idomnál. Mégis, a méhek ,,mentségére'' meg kell jegyeznünk, hogy az utóbbi zárólaprendszer esetében a cella teljes felszíne alig

3, 3 ‰

-kel kisebb, mint a méheknél (ugyanis a bevezetőben közölt, mért értékekkel

a = 11, 3 / 2, 7 = 4, 2

), továbbá hogy a négytagú zárólaprendszer építése bonyolultabb lenne (

2

-féle lapalak, a lap- és élszögeket nem is számítottuk).
6. Lehet-e tovább javítani a sejtidom négytagú zárólaprendszerének méreteit ? Kiderül, hogy a 7. ábra

X A = x

méretének változtatásával lehet, bár ismét csak kis mértékben. Így az idom felszíne

\begin{matrix} G (x) = 6 a - 4 x + \frac{1}{4} \sqrt[]{48 x^{2} + 3} + \frac{5}{4} \sqrt[]{16 x^{2} + 3}, \end{matrix}

amiből a fenti vizsgálathoz hasonlóan

\begin{matrix} G' (x) = 4 (\frac{3 x}{\sqrt[]{48 x^{2} + 3}} + \frac{5 x}{\sqrt[]{16 x^{2} + 3}} - 1) = 4 (\frac{3}{\sqrt[]{48 + \frac{3}{x^{2}}}} + \frac{5}{\sqrt[]{16 + \frac{3}{x^{2}}}} - 1), \end{matrix}

G' (0) = - 4

és

x > 0

esetén

G' (x)

monoton nő, a

G' (x) = 0

egyenlet gyöke ^{$^{*}$}

x = 0, 279 ...

, itt

G' (x)

negatívból pozitívba, maga

G (x)

pedig csökkenésből növekedésbe vált át, itt van az egyetlen minimum, melynek értéke

G (0, 279) = 6 a + 2, 1092

, a méhekénél

4, 5 ‰

-kel kevesebb.
Nincs bebizonyítva, de valószínű, hogy az így kapott zárólaprendszer (alább új idomnak nevezzük) nem javítható tovább ‐ ti. a zárólapok minőségileg más megválasztásával ‐, más szóval a felhasznált viaszmennyiség szempontjából ez a leggazdaságosabb zárólaprendszer.
7. Befejezésül nézzük még meg, hogyan alakul három eredményünk, ha ‐ a méhészek ismert módján ‐ műléppel könnyítjük a méhek munkáját, viasztermelés helyett a mézgyűjtés felé irányítva őket. A műlép készen adja a méheknek a zárólaprendszert, kb.

20 \times 30 cm

méretű ,,recézett'' lemezként, és ehhez csak az oldalfalakat kell megépíteniük. Mennyiségben ez még mindig a nagyobb része a munkának, de egyúttal bizonyára az egyszerűbb része is. Táblázatunkban az említett

a = 4, 2

érték alapulvételével felírtuk a sejt összfelszínét (a bemeneti nyílás nélkül) és ennek megoszlását zárólaprendszerre és oldalfalakra. Így a megépítendő palástfelszín tekintetében a méhek a rangsor középső helyét foglalják el, az új idom a legjobb, mert

x

-nek

0, 25

-ről

0, 279

-re emelésével a zárólapok meredekebbek, felszínük nő, tehát nagyobb a felszínnek műléppel előkészíthető része.

\begin{matrix} 1 sejt összfelszíne & Zárólaprendszer & Palást felszíne \\ felszíne \\ Méhek: & 27,2324 & 3,1820 & 24,0504 \\ Négyzárólapú \\ idom: & 27,2235 & 3,1124 & 24,1111 \\ Új-idom: & 27,2203 & 3,2260 & 23,9943 \end{matrix}

Érdekes geometriai-biológiai kísérlet lenne a méheknek Fejes-Tóth-féle vagy új idomú műlépeket bekészíteni, vajon hogyan csatlakoztatnák a hatoldalú palástokat a

10

tagú koronavonalhoz.

Csákány Béla ^{$^{*}$}

^{$^{*}$}Lásd pl. H. Dörrie: A diadalmas matematika. Gondolat Kiadó. Budapest, 1965. 384. oldal. ‐ Móra Ferenc: A világ így megyen. Szépirodalmi Kiadó. Budapest, 1956. 162‐165. oldal.

^{$^{*}$}L. Fejes Tóth: What the bees know and what they do not know. Bulletin of the American Mathematical Society, 70 (1964) pp. 468‐481. (Magyarul: Mi az, amit tudnak a méhek és mi az, amit nem tudnak.)

^{$^{*}$}A $G' (x) = 0$ egyenletből a gyökmennyiségeket a szokásos módon eltüntetve negyedfokú egyenletet kellene megoldanunk. Emiatt célszerűbb közelítő eljárást alkalmaznunk a következő módon. Észrevesszük, hogy $G' (0) < 0$ , $G' (1) > 0$ ; így $0$ és $1$ között a $G' (x) = 0$ egyenletnek van megoldása. Továbbá $G' (\frac{1}{2}) > 0$ , így $0$ és $\frac{1}{2}$ között van megoldás. Ezt a eljárást folytatva, az $n$ -edik lépésben a megoldást $\frac{1}{2^{n - 1}}$ hosszúságú intervallumba szoríthatjuk. Így nyertük az $x = 0, 279 ...$ értéket.

^{$^{*}$}Köszönetet mondok a Szerkesztőség tagjainak: Bakos Tibornak, volt tanáromnak, e cikk elkészítéséhez nyújtott önzetlen segítségéért és Matavovszky Tibornak értékes megjegyzéséért. A szerző.