Kezdőlap


Cím:	A vastag lencsék
Szerző(k):	Vermes Miklós
Füzet:	1967/november, 163 - 166. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A lencsék működését a fénytörés törvénye magyarázza meg. A tárgy valamely pontjából kiinduló fénysugarak mindegyike a lencsén áthaladva kétszer törik meg és a lencsén átment sugarak újra egyetlen pontban találkoznak. A tárgy lencsétől mért $t$ távolsága a tárgytávolság, a kép $k$ távolsága a képtávolság. A tengellyel párhuzamosan beeső sugarak találkozási pontja a fókusz, ennek a lencsétől mért $f$ távolsága a fókusztávolság. A lencse anyagának $n$ törésmutatójából és határoló gömbfelületeinek $r_{1}$ , $r_{2}$ rádiuszaiból kiszámítható a fókusztávolság: $1 / f = (n - 1) (1 / r_{1} + 1 / r_{2})$ , továbbá érvényes a képalkotás törvénye: $1 / f = 1 / t + 1 / k$ . E két képlet a fénytörés törvényéből vezethető le, de csak közelítően érvényes akkor, ha a fénysugarak a tengely közelében haladnak, ha az előforduló beesési és törési szögek kicsinyek, ha a törésmutató nem függ a hullámhossztól és ha a lencse elhanyagolható vastagságú. Ilyen vékony lencsénél elegendő az az utasítás, hogy $f$ , $t$ , $k$ ,,a lencsétől'' mérendők.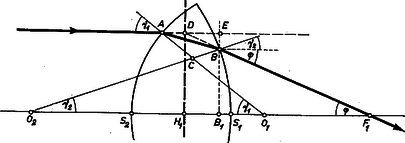
A lencse véges vastagságát számítással könnyen figyelembe lehet venni. Ekkor kapjuk a véges vastagságú lencsére érvényes képleteket. De a többi közelítés szükségessége most is megmarad! Lássuk ezt a számítást!

1. ábra

A lencse felületeinek rádiuszai

r_{1} = A O_{1}

és

r_{2} = B O_{2}

, vastagsága

d = S_{1} S_{2}

, anyagának törésmutatója

n

(1. ábra). A tengellyel párhuzamosan beeső fénysugár

A

-ban éri el az első lencsefelületet, itt megtörik,

B

-be érkezik és ismét törik. A lencsét elhagyó fénysugár

F_{1}

fókuszpontban metszi a tengelyt. Ábránk vastag vonala a fénysugár tényleges útját tünteti fel. Hosszabbítsuk meg a belépő és kilépő fénysugarak egyeneseit: megkapjuk ezek

D

metszéspontját. Formálisan, szerkesztés alkalmával úgy vesszük, mintha a vízszintesen haladó fénysugár

D

-ben változtatta volna meg haladási irányát. A rádiuszok tengellyel alkotott szögei

γ_{1}

és

γ_{2}

, a kilépő sugár tengellyel alkotott szöge

φ

; ezeket a szögeket a rajzban még több helyen is megtaláljuk. Közelítéseink miatt csak kis szögek szerepelhetnek, ezért az üvegben mért törési szögeket a törésmutatóval való osztással kapjuk meg:

B A C ∢ - γ_{1} / n

és

A B C ∢ = (γ_{2} + φ) / n

. Az

A B C_{▵}

és az

O_{1} C O_{2 ▵}

tompaszöge egyenlő, tehát két-két hegyes szögének összege is egyenlő:

\begin{matrix} γ_{1} + γ_{2} = \frac{γ_{1}}{n} + \frac{γ_{2} + φ}{n} . \end{matrix}

Ebből az egyenletből:

\begin{matrix} φ = (n - 1) (γ_{1} + γ_{2}) . \end{matrix}

(1)

Ez az egyenlet teszi lehetővé a fókusztávolság kiszámítását, ha a szögekről távolságokra térünk át.
Az

F_{1}

fókuszpont távolságát mérjük

H_{1}

-től, vagyis a

D

ponton átmenő függőleges síktól:

f = H_{1} F_{1}

. A szögeket radiánokban számítjuk. Ha kicsinyek, akkor írható, hogy

φ = D H_{1} / f

γ_{1} = D H_{1} / r_{1}

és

γ_{2} = B B_{1} / r_{2}

. Így az (1) egyenlet:

\begin{matrix} \frac{D H_{1}}{f} = (n - 1) [\frac{D H_{1}}{r_{1}} + \frac{B B_{1}}{r_{2}}], \end{matrix}

illetve:

\begin{matrix} \frac{1}{f} = (n - 1) [\frac{1}{r_{1}} + \frac{B B_{1}}{D H_{1}} \cdot \frac{1}{r_{2}}] . \end{matrix}

(2)

Számításainkra az lesz jellemző, hogy a tengellyel párhuzamos távolságok (például

B_{1} S_{1}

) tekintetében elhanyagolunk, hiszen számításunk csak a tengely közelében haladó sugarakat vesz figyelembe, de a tengelyre merőleges irányban pontosan számolunk. Ennek oka, hogy a fénysugarakkal a tengely felé haladva a tengellyel párhuzamos irányban elkövetett elhanyagolások sokkal gyorsabban közelednek nullához, mint a tengelyre merőleges irányban elkövetett közelítések. Ez az ábrából is felismerhető, hiszen a körív

B_{1} S_{1}

eltérése az érintőtől négyzetesen csökken, ha a sugárral közeledünk a tengelyhez, viszont

E B

igen nagy lehet vastag lencséknél. Így

B B_{1}

-et és

D H_{1}

-et nem vehetjük egyenlőnek, a

B B_{1} / D H_{1}

törtet ki kell számítanunk.
A

B A E

derékszögű háromszögből

B E = A B sin B A E ∢

. Az

A B

távolságot közelítően

d = S_{1} S_{2}

lencsevastagsággal, a szög színuszát a radiánban számolt szöggel vesszük egyenlőnek:

B A E ∢ = C A E ∢ - C A B ∢ = γ_{1} - γ_{1} / n

. Ennek alapján

B E = d (γ_{1} - γ_{1} / n) = d γ_{1} (n - 1) / n = D H_{1} \cdot d (n - 1) / (r_{1} n)

és

B B_{1} = D H_{1} - B E = D H_{1} - D H_{1} \cdot d (n - 1) / (r_{1} n)

, így:

\begin{matrix} \frac{B B_{1}}{D H_{1}} = 1 - d \cdot \frac{n - 1}{n} \cdot \frac{1}{r_{1}} . \end{matrix}

(3)

Ezt (2)-be helyettesítve kapjuk a fókusztávolság képletét abban az esetben, ha a lencse vastagságát figyelembe vesszük:

\begin{matrix} \frac{1}{f} = (n - 1) [\frac{1}{r_{1}} + \frac{1}{r_{2}} - d \cdot \frac{n - 1}{n} \cdot \frac{1}{r_{1} r_{2}}] . \end{matrix}

(4)

A fénysugár magasságát megadó

D H_{1}

távolság kiesése azt jelenti, hogy minden párhuzamosan beeső fénysugár

F_{1}

-ben találkozik, amennyiben közelítéseink teljesülnek.
Szükségünk van még a

d_{1} = H_{1} S_{1}

távolságra, hogy tudjuk, honnan kell mérni a fókusztávolságot. A

B E D

derékszögű háromszögből:

\begin{matrix} D E = B E / φ = (D B_{1} - B B_{1}) / φ = f (1 - \frac{B B_{1}}{D H_{1}}) . \end{matrix}

Ide

f

(2) alatti és

B B_{1} / D H_{1}

(3) alatti értékeit helyettesítve:

\begin{matrix} d_{1} = \frac{d r_{2}}{n (r_{1} + r_{2}) - d (n - 1)} . \end{matrix}

(5)

D H_{1}

sík neve fősík, a kilépő lencsefelülettől mért

d_{1}

távolságát ez a képlet adja meg. Ha a fény a tengellyel párhuzamosan jobbról jön, akkor az indexek felcserélésével a második fősík távolsága a bal oldali felülettől:

\begin{matrix} d_{2} = \frac{d r_{1}}{n (r_{1} + r_{2}) - d (n - 1)} . \end{matrix}

(5')

A fókusztávolság (4) alatti képletében az indexek szimmetrikusan fordulnak elő, tehát a fókusztávolság mindegyik oldalon ugyanakkora. Természetesen

d = 0

esetében a vékony lencsék közismert képletei adódnak.
1. ábránk pontos rajz abban az esetben, ha

n = 1, 5

. A rádiuszok

r_{1} = 4 cm

és

r_{2} = 6 cm

d = 3 cm

. A fókusztávolság

f = 16 / 3 = 5, 33 cm

, a fősíkok távolságai

d_{1} = 4 / 3 = 1, 33 cm

és

d_{2} = 8 / 9 = 0, 89 cm

d = 0

esetében lencsénk fókusztávolsága

4, 8 cm

lenne. Az eltérés nem túlságosan sok, de nem tudnánk, honnan mérjük a fókusztávolságot.
Mindezek alapján egy vastag lencsénél következőképp kell eljárnunk. Először kiszámítjuk (5) és (

5'

) alapján

d_{1}

-et és

d_{2}

-t.

d_{1}

-et a kilépő felülettől balra,

d_{2}

-t a belépő felülettől jobbra mérjük fel és megkapjuk

H_{1}

H_{2}

fősíkok helyét. Azután kiszámítjuk (4) szerint a fókusztávolságot;

f

-et

H_{1}

-től jobbra felmérve

F_{1}

-et,

H_{2}

-től balra felmérve

F_{2}

-t kapjuk meg. Ha

d_{1}

d_{2}

f

közül valamelyik negatív, az irányt fordítva kell venni.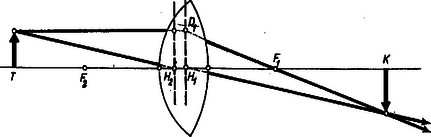

2. ábra

2. ábránk az 1. ábra lencséjére vonatkozik, de felére kicsinyítve. Az adott

T

tárgyról az egyik szerkesztési sugarat a tengellyel párhuzamosan addig rajzoljuk, amíg eléri az első fősíkot

D_{1}

-ben; a kilépő sugarat

F_{1}

-en keresztül rajzoljuk. A második szerkesztési sugarat

H_{2}

-nek irányítjuk és önmagával párhuzamosan eltolva folytatjuk

H_{1}

-ből. A kilépő sugarak metszéspontja adja meg

K

képet. A tárgytávolság a második, a képtávolság az első fősíktól mérendő:

t = T H_{2}

k = H_{1} K

; ezekre a távolságokra teljesül az

1 / t + 1 / k = 1 / f

lencsetörvény. A helyzet kb. olyan, mintha a görbült lencsefelületek közé egy planparalel lemezt toltunk volna be. Eljárásunkkal a lencse vastagságának szerepét pontosan figyelembe vettük, de a többi közelítés feltétele megmarad, és a lencsehibák ugyancsak fellépnek. Lássunk néhány példát vastag lencsékre.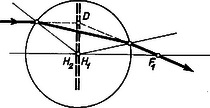

3. ábra

1. Gömb mint lencse (3. ábra). Ekkor

r_{1} = r_{2} = r

d = 2 r

; képleteink szerint

f = n r / 2 (n - 1)

d_{1} = d_{2} = r

. Tehát mindkét fősík a középpontba kerül. Ha a lencse anyaga

1, 5

-es törésmutatójú üveg, akkor

f = 1, 5 r

, ha víz, akkor

n = 4 / 3

és

f = 2 r

, mindegyik esetben a középponttól mérve. Mindez hengerlencsére is érvényes és vízzel, folyadékkal telt gömblombikkal, hengerpohárral kivizsgálható.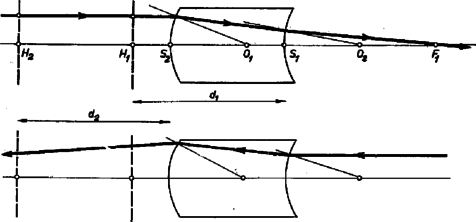

4. ábra

2. Álljon lencsénk két egyező rádiuszú, ellentétes görbületű gömb- vagy hengerfelületből (4. ábra). Ha a felületek közel vannak, akkor a szerkezet planparalel lemezként viselkedik, de ha vastagsága nagy, akkor lencseként működik. Ekkor

r_{1} = r

r_{2} = - r

, így

f = n r^{2} / d {(n - 1)}^{2}

d_{1} = r / (n - 1)

d_{2} = - r / (n - 1)

. 4. ábránkon

r = 2 cm

n = 1, 5

d = 1, 5 r

d_{1} = 2 r

d_{2} = - 2 r

f = 4 r

. Tanulságos a fordított irányú sugármenet tanulmányozása is (alsó rajz).

Vermes Miklós